Rzut (matematyka)
|
Read other articles:

Saʿad I al-ʿAbd Allāh Al Sālim Al ṢabāḥEmiro del KuwaitStemma In carica15 gennaio –24 gennaio 2006 PredecessoreJaber III Al-Ahmad Al-Jaber SuccessoreṢabāḥ IV Al Aḥmad al-Jāber Altri titoliSceicco NascitaMadinat al-Kuwait, 1929 MorteMadinat al-Kuwait, 13 gennaio 2008 Luogo di sepolturaCimitero di Al Sulaibikhat, Madinat al-Kuwait Casa realeAl Sabah PadreʿAbd Allāh III Al Sālim Al Ṣabāḥ MadreSceicca Jamila (concubina) ConsorteSceicca Latifa bint Fahad Al Sa...

Dynastic chivalric order of the House of Bourbon-Two Sicilies For other uses, see Order of Saint George (disambiguation). Sacred Military Constantinian Order of Saint George Cross of the orderFoundedc. 1545 (actual)Royal house Bourbon-Two Sicilies Bourbon-ParmaReligious affiliationCatholicSeatBasilica of the Holy Cross in Via Flaminia, RomeRibbonLight blueMottoIn hoc signo vincesFounderConstantine the Great (legendary)Andrea Angelo Flavio Comneno (actual)Grand MasterDisputed:Prince Pedro...

معركة مري جزء من الحروب المملوكية الأرمينية المماليك يهزموا الأرمن في معركة مري في 1266 ويقتلوا توروس أحد أبناء الملك حيطوم الأول (الساقط على الأرض، جهة اليمين) ويأسروا ابنه الآخر (الملك المستقبلي ليو الثاني، في المنتصف).[1] معلومات عامة التاريخ 24 أغسطس 1266 البلد مملكة أرم�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أغسطس 2014) شلالات مونتمورنسيمعلومات عامةالمكان مدينة كيبكبواشاتل البلد كندا المستجمع المائي estuary basin of the Saint Lawrence River (en) المجرى المائي Rivière Montmorency (en) — site patrimonial de la Chute-M...

Front Fatah al-Cham Front al-Nosraجبهة النصرة لأهل الشامFront Fatah al-Chamجبهة فتح الشام Idéologie Salafisme djihadiste[1] Objectifs Instauration d'un califat régi par la charia Statut Inactif Fondation Date de formation 24 janvier 2012(Front al-Nosra)28 juillet 2016(Front Fatah al-Cham) Dissolution Date de dissolution 28 janvier 2017 Causes Fusion avec le Harakat Nour al-Din al-Zenki, le Front Ansar Dine, le Liwa al-Haq, Jaych al-Sunna et Jaych al-Ahrar pour...

Імператор Тьокейяп. 長慶天皇Народився 1343[1]Помер 27 серпня 1394Країна ЯпоніяДіяльність суверенЗнання мов японськаПосада імператор ЯпоніїРід Імператорський дім ЯпоніїБатько Імператор Ґо-МуракаміМати Kakimon-indБрати, сестри Moronari-shinnōd, Korenari-shinnōd, Yoshinari-shinnōd, Kanenari-shinnōd,&#...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (novembre 2020). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références » En pratique : Quelles sources sont attendues ? C...

Microsoft Photo EditorCuplikan pengoperasian Photo Editor dalam Windows XPPengembangMicrosoftRilis stabil3.0.2.3 / 15 Desember 2000 Sistem operasiMicrosoft WindowsJenisRaster graphics editorLisensiProprietarySitus webMicrosoft Photo Editor KB article Microsoft Photo Editor adalah aplikasi manipulasi gambar untuk Windows 97–XP. Program ini telah digantikan oleh Microsoft Office Picture Manager, walaupun beberapa fitur Photo Editor tidak terdapat dalam Picture Manager.[1] Referensi ^ ...

El White Knight es una aeronave usada como lanzadera del SpaceShipOne. Fue desarrollado por Scaled Composites como parte de su programa Tier One y ofrecida posteriormente como avión de pruebas para el planeador espacial Boeing X-37 desde junio de 2005 hasta abril de 2006. Historia El White Knight cargando al SpaceShipOne. El White Knight es el modelo número 318 de Scaled Composites y está registrado como N318SL en la Administración Federal de Aviación de Estados Unidos. Su primer vuelo s...

贵州省革命委员会 主要领导 主任 李再含 → 蓝亦农 → 鲁瑞林 → 马力 机构概况 上级机构 中华人民共和国国务院贵州省人民代表大会(瘫痪) 机构类型 省级革命委员会 行政级别 正省级 授权法源 1975年《中华人民共和国宪法》和1978年《中华人民共和国宪法》 联络方式 总部 机构沿革 1949年12月 贵州省人民政府 1955年2月 贵州省人民委员会 1967年2月 贵州省革命委员会 1980年1�...

Constitutional and hereditary monarchy of the Kingdom of the Netherlands Queen of the Netherlands redirects here. For the ship, see Queen of the Netherlands (ship). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article's tone or style may not reflect the encyclopedic tone used on Wikipedia. See Wikipedia's guide to writing better articles for suggestions. (March 2023) (Learn how an...

Untuk orang lain dengan nama yang sama, lihat John Roberts. John RobertsPotret Resmi, 2005Ketua Mahkamah Agung Amerika Serikat Ke-17PetahanaMulai menjabat 29 September, 2005Dicalonkan olehGeorge W. BushPendahuluWilliam RehnquistHakim dari Pengadilan Banding Amerika Serikat untuk Distrik Sirkuit ColumbiaMasa jabatan2 Juni, 2003 – 29 September, 2005Dicalonkan olehGeorge W. BushPendahuluJames L. BuckleyPenggantiPatricia MillettWakil Jaksa Agung Amerika SerikatMasa jabatanOctob...

Capital of Nakhchivan, Azerbaijan City in Nakhchivan, AzerbaijanNakhchivan NaxçıvanCityLandmarks of Nakhcivan, from top left:Garabaghlar Mausoleum • Khan PalaceNakhcivan Hospital • Momine KhatunCity Centre • Juma MosqueFeminine Centre • Nakhcivan MountainsNakhchivanCoordinates: 39°12′58″N 45°24′38″E / 39.21611°N 45.41056°E / 39.21611; 45.41056Country AzerbaijanAutonomous RepublicNakhchivanArea • Total190 k...

PalomonteKomuneComune di PalomonteLokasi Palomonte di Provinsi SalernoNegara ItaliaWilayah CampaniaProvinsiSalerno (SA)Luas[1] • Total28,3 km2 (10,9 sq mi)Ketinggian[2]550 m (1,800 ft)Populasi (2016)[3] • Total4.049 • Kepadatan140/km2 (370/sq mi)Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos84020Kode area telepon0828Situs webhttp://www.comune.palomonte.sa.it Palomonte...
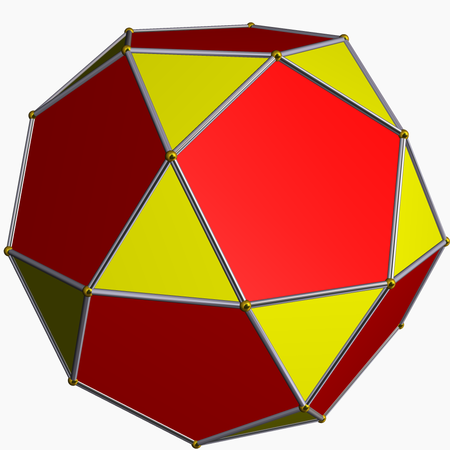
Notation for a polyhedron's vertex figure Icosidodecahedron Vertex figure represented as3.5.3.5 or (3.5)2 In geometry, a vertex configuration[1][2][3][4] is a shorthand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron. (Chiral polyhedra exist in mirror-image pairs with the same ver...

American baseball player (born 1987) Baseball player Ryan BuchterBuchter with the Athletics in 2019PitcherBorn: (1987-02-13) February 13, 1987 (age 36)Reading, Pennsylvania, U.S.Batted: LeftThrew: LeftMLB debutJune 20, 2014, for the Atlanta BravesLast MLB appearanceAugust 1, 2021, for the Arizona DiamondbacksMLB statisticsWin–loss record17–6Earned run average3.16Strikeouts259 Teams Atlanta Braves (2014) San Diego Padres (2016–2017) Kansas City Royals (...

Some popular landscapes of Afghanistan, from left to right: 1. Band-e Amir National Park; 2. Salang Pass in Parwan Province; 3. Korangal Valley in Kunar Province; and 4. Kajaki Dam in the valley of Helmand Province Foreign tourists in Kabul, c. 1940 Tourism in Afghanistan is regulated by the Ministry of Information and Culture. There are at least 350 tourism companies operating in Afghanistan.[1] Tourism was at its peak before the 1978 Saur Revolution, which was followed by the decade...

Islamic religious seminary in northern Pakistan This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: wrong use of bold text, repetitive linking, broken English, too much biographical information. Please help improve this article if you can. (February 2022) (Learn how and when to remove this template message) Darul Uloom Haqqaniaدار العلوم حقانیہTypeIslamic UniversityMadrasaDarul UloomEstablished23 September 1947; 76 years...

Australian rules footballer Australian rules footballer Sam Jacobs Jacobs playing for Adelaide in April 2017Personal informationFull name Sam JacobsNickname(s) SauceDate of birth (1988-04-10) 10 April 1988 (age 35)Place of birth Ardrossan, South AustraliaOriginal team(s) Ardrossan Kangaroos/Woodville-West Torrens (SANFL)Draft No. 1, 2007 Rookie DraftDebut Round 1, 2009, Carlton vs. Richmond, at MCGHeight 202 cm (6 ft 8 in)Weight 102 kg (225 lb)Position(...

Hierdie artikel handel oor die taal. Vir die etniese groep, sien Perse. Persies فارسی fārsi Gepraat in: Iran Afghanistan Tadjikistan Oesbekistan Turkmenistan Pakistan Indië Gebied: Suid-Asië Totale sprekers: 57 miljoen[1] Taalfamilie: Indo-Europees Indo-Irannees Irannees Persies Skrifstelsel: Arabiese alfabet Amptelike status Amptelike taal in: Iran as Farsi Afghanistan ...



















