Een splayboom is een zelf-balancerende binaire zoekboom, met de extra eigenschap dat vaak bezochte toppen dichter bij de wortel zitten (en dus sneller gevonden worden). Standaardbewerkingen zoals toevoegen, opzoeken en verwijderen van een top worden uitgevoerd in O(n) tijd voor één bewerking, maar geamortiseerd in O(log(n)) tijd voor een reeks van n bewerkingen. Voor vele niet (volledig) willekeurig reeksen van bewerkingen presteren splaybomen beter dan standaard binaire zoekbomen, voornamelijk wanneer een relatief kleine deelverzameling van de toppen van de boom vaak bezocht worden.
Alle bewerkingen op een splayboom worden uitgevoerd zoals bij een normale binaire zoekboom, maar ze worden gevolgd door een splaystap.
De splayboom is ontwikkeld door Daniel Sleator en Robert Tarjan
Bottom-up en Top-down
Bij "Bottom-up" splayen zal de bewerking uitgevoerd worden, en tegelijk wordt het pad naar de bezochte top bijgehouden. Nadat de bewerking is uitgevoerd, zal het pad helemaal gesplayed worden, van onder naar boven. Om het pad op te slaan, wordt vaak een stack-datastructuur gebruikt, waar voor de splaystap dan telkens de laatste 3 toppen van ge-pop()'t worden, en de nieuwe wortel van deze deelboom met die 3 toppen wordt terug op de stack ge-push()'t.
Bij "Top-down" splayen zal, telkens wanneer 3 niveaus (toppen) afgedaald wordt, die 3 toppen gesplayed worden. De laatste top wordt ook weer hergebruikt om de deelboom met de volgende 3 toppen te construeren.
Top-down implementaties zullen dus typisch ongeveer dubbel zo snel zijn dan bottom-up implementaties, aangezien niet telkens het hele pad naar de laatste top eerst opgebouwd moet worden, en daarna weer helemaal afgelopen om te splayen.
De splaystap
Het pad wordt zo lang mogelijk gesplayed per 3 toppen (de laatste top x, zijn ouder p, en de ouder van p, genaamd g), enkel wanneer op het einde nog slechts 2 toppen beschikbaar zijn kan met 2 toppen gesplayed worden (dit komt enkel voor wanneer het (volledige) pad naar het opgezochte element in de boom een even aantal toppen bevat).
Er zijn in totaal 6 gevallen te onderscheiden, "zig-zig", "zig-zag", "zig" en hun spiegelbeelden "zag-zag", "zag-zig" en "zag". We bespreken enkel de eerste 3, de andere zijn volledig analoog:
Zig-zig stap: hier is x een linkerkind van p, en p een linkerkind van g. Noem het linkerkind van x b1, het rechterkind van x b2, het rechterkind van p b3 en het rechterkind van g b4.
Nu maken we x de nieuwe wortel, b1 blijft een linkerkind van x, en p wordt het nieuwe rechterkind van x. g wordt het nieuwe rechterkind van p. Het nieuwe linkerkind van p is b2, en het nieuwe linkerkind van g is b3. b4 blijft het rechterkind van g.
![]()
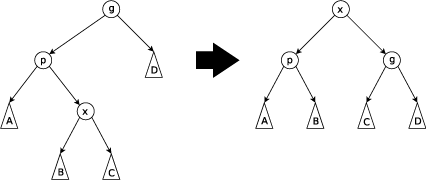
Zig-zag stap: hier is x een rechterkind van p, en p een linkerkind van g. Noem het linkerkind van p b1, het linkerkind van x b2, het rechterkind van x b3 en het rechterkind van g b4.
Nu maken we x de nieuwe wortel, p wordt het linkerkind van x en g wordt het rechterkind van x. b1 blijft het linkerkind van p, b2 wordt het rechterkind van p, b3 wordt het linkerkind van g en b4 blijft het rechterkind van g.
Zig stap: hier is er geen g, enkel een ouder p met als linkerkind x. Noem het linkerkind van x b1, het rechterkind van x b2, en het rechterkind van p b3. We maken x de nieuwe wortel, b1 blijft het linkerkind van x en b3 blijft het rechterkind van p, maar het nieuwe linkerkind van x is p, en het nieuwe rechterkind van p is b2.

Merk op dat de buitenbomen van het deelpad van 2 of 3 nodes (dus deelbomen van de 'grote' boom met als wortel b1, b2, b3 en b4) ook NULL mogen zijn, m.a.w. het maakt niet uit of het x een blad is of 1 of 2 kinderen heeft.
Semi-splay
Een kleine variant op splayen is deze semi-splay, waarbij de bezochte top dus niet de wortel van de gesplayde boom kan worden als er een zig-zig of een zag-zag bewerking is gebeurd tijdens het splayen van het pad. Het verschil met standaard splayen zit namelijk in deze bewerking:
Zig-zig stap: hier is x een linkerkind van o, en o een linkerkind van g. Noem het linkerkind van x b1, het rechterkind van x b2, het rechterkind van o b3 en het rechterkind van g b4.
Nu maken we o de nieuwe wortel, x blijft een linkerkind van o, maar g wordt het nieuwe rechterkind van o. b1 en b2 blijven de kinderen van x, maar b3 en b4 worden de kinderen van g.
Externe links
Het algoritme
Implementaties
Visualisaties