–Ъ—Г–њ –љ–∞ —И–∞–Љ–њ–Є–Њ–љ–Є 1968/69
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

–Я–ї–µ–љ—Г–∞Plesnois –Ъ—А–∞—Ч–љ–∞ –§—А–∞–љ—Ж—Ц—П –†–µ–≥—Ц–Њ–љ –У—А–∞–љ–і-–Х—Б—В –Ф–µ–њ–∞—А—В–∞–Љ–µ–љ—В –Ь–Њ–Ј–µ–ї—М –Ю–Ї—А—Г–≥ –Ь–µ—Ж –Ъ–∞–љ—В–Њ–љ –Ь–∞—А–∞–љ–ґ-–°—М–є–≤–∞–љ–ґ –Ъ–Њ–і INSEE 57546 –Я–Њ—И—В–Њ–≤—Ц —Ц–љ–і–µ–Ї—Б–Є 57140 –Ъ–Њ–Њ—А–і–Є–љ–∞—В–Є 49¬∞10вА≤23вА≥ –њ–љ. —И. 6¬∞06вА≤24вА≥ —Б—Е. –і.H G O –Т–Є—Б–Њ—В–∞ 188 - 376 –Љ.–љ.—А.–Љ. –Я–ї–Њ—Й–∞ 3,11 –Ї–Љ¬≤ –Э–∞—Б–µ–ї–µ–љ–љ—П 803 (01-2020[1]) –У—Г—Б—В–Њ—В–∞ 249,84 –Њ—Б./–Ї–Љ¬≤ –†–Њ–Ј–Љ—...

ўБўКЎ±ўИўЖўКўГЎІ ўБўИЎ≥Die Sehnsucht der Veronika Voss (Ў®ЎІўДЎ£ўДўЕЎІўЖўКЎ©) ўЕўДЎµўВ ЎІўДўБўДўЕўЕЎєўДўИўЕЎІЎ™ ЎєЎІўЕЎ©ЎІўДЎµўЖўБ ЎІўДўБўЖўК ўБўКўДўЕ ЎѓЎ±ЎІўЕЎІ[1][2] вАФ ўБўДўЕ ўБўЖўК ЎІўДўЕўИЎґўИЎє ЎІўЖЎ™Ў≠ЎІЎ± Ў™ЎІЎ±ўКЎЃ ЎІўДЎµЎѓўИЎ± 1982 18 ўБЎ®Ў±ЎІўКЎ± 1982[3] (Ў£ўДўЕЎІўЖўКЎІ) ўЕЎѓЎ© ЎІўДЎєЎ±Ўґ 100 ЎѓўВўКўВЎ© ЎІўДўДЎЇЎ© ЎІўДЎ£ЎµўДўКЎ© ЎІўДЎ£ўДўЕЎІўЖўКЎ© ЎІўДЎєЎ±Ўґ Ў£Ў®ўКЎґ ўИЎ£Ў≥ўИЎѓ ЎІўДЎ®ўДЎѓ Ў£ўДўЕЎІўЖўКЎІ ЎІўДЎђўИЎІЎ¶Ў≤ ЎІўДЎѓЎ® ЎІўДЎ∞ўЗЎ®ўК (1982) ЎІўДЎЈ

Vlaamse overheid Geschiedenis Opgericht 1980 Voorganger(s) 1981-1991: Ministerie van de Vlaamse Gemeenschap Geschiedenis Jurisdictie Vlaanderen Aantal werknemers 28.704 (2021) Media Website https://www.vlaanderen.be De Vlaamse overheid is de offici√Ђle overheid binnen de Belgische deelstaat Vlaanderen. Ze omvat het Vlaams Parlement, de Vlaamse Regering en de overheidsdiensten. Structuur Vlaams Parlement Zie Vlaams Parlement voor het hoofdartikel over dit onderwerp. Het Vlaams Parlement te Bru...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: School of Fontainebleau вАУ news ¬Ј newspapers ¬Ј books ¬Ј scholar ¬Ј JSTOR (December 2009) (Learn how and when to remove this template message) Diana the Huntress - School of Fontainebleau, 1550вАУ1560, (Louvre) The School of Fontainbleau (French: √Йcole de Fontaine...

President van Armeni√Ђ ’А’°’µ’°’љ’њ’°’ґ’Ђ ’А’°’ґ÷А’°’Ї’•’њ’Є÷В’©’µ’°’ґ ’Ж’°’≠’°’£’°’∞ Kantoor Aanspreekvorm Zijne excellentie Residentie Presidentieel paleis,Jerevan Ambtstermijn Vijf jaar, √©√©n keerherkiesbaar Geschiedenis Eerste Levon Ter-Petrosian Ontstaan in 11 november 1991 Huidige Vahagn Khachaturian Sinds 13 maart 2022 Portaal Politiek Hieronder staat een chronologische lijst van presidenten van Armeni√Ђ, inclusief de lijst van staatshoofden van diens voorloper de Democra...

Sofyan Chalid bin Idham Ruray (lahir 28 September 1980) adalah seorang ustad Indonesia. Lahir di Manado, Ia pernah mengajar di Majelis TaвАЩlim Forum Studi dan Dakwah Islam Manado, Majelis TaвАЩlim As-Sunnah Ternate, Madrasah As-Salafiyyah Depok dan lainnya. Sementara itu, ia juga menulis buku di antaranya Salafi, Antara Tuduhan dan Kenyataan, Tauhid Pilar Utama Membangun Negeri, Madrasah Ramadhan dan yang lainnya.[1] Referensi ^ https://www.boombastis.com/ustaz-sofyan-chalid/294881 A...

American former basketball player (born 1952) For other people named Ron Lee, see Ronald Lee (disambiguation). Ron LeeRon Lee, 1977Personal informationBorn (1952-11-02) November 2, 1952 (age 71)Boston, Massachusetts, U.S.NationalityAmericanListed height6 ft 4 in (1.93 m)Listed weight193 lb (88 kg)Career informationHigh schoolLexington (Lexington, Massachusetts)CollegeOregon (1972вАУ1976)NBA draft1976: 1st round, 10th overall pickSelected by the Phoenix SunsPlayin...

Japanese manga series Boys Be...First tank≈Нbon volume coverGenreComing-of-age[1]Romantic comedy[2][3]Slice of life[1][4] MangaWritten byMasahiro ItabashiIllustrated byHiroyuki TamakoshiPublished byKodanshaEnglish publisherNA: Tokyopop[a]ImprintSh≈Нnen Magazine ComicsMagazineWeekly Sh≈Нnen MagazineDemographicSh≈НnenOriginal runAugust 7, 1991 вАУ March 14, 2001Volumes58 Series titles Boys Be... (1991вАУ1996; 32 volumes) Boys Be... ...

MLB Playoff matchup between the Houston Astros and New York Yankees 2019 American League Championship Series Team (Wins) Manager(s) Season Houston Astros (4) A. J. Hinch 107вАУ55 (.660), GA: 10 New York Yankees (2) Aaron Boone 103вАУ59 (.636), GA: 7DatesOctober 12вАУ19MVPJos√© Altuve (Houston)UmpiresDan Bellino, Cory Blaser, Mark Carlson, Kerwin Danley, Mike Everitt (crew chief, Games 4вАУ6),[a] Marvin Hudson,[b] Jeff Nelson (crew chief, Games 1вАУ3),[a] Bill Welke[...

Ancient Greek city, forerunner of Constantinople This article is about the ancient city. For the city in the late Roman period (330вАУ1453), see Constantinople. For the Ottoman and modern city (after 1453), see Istanbul. For the empire, see Byzantine Empire. For other uses, see Byzantium (disambiguation). ByzantiumByzantionLocation of Byzantion, corresponding to the modern-day Fatih district of IstanbulAlternative nameByzantion (earlier Greek name), Nova Roma (New Rome)LocationFatih, Ist...

–°–∞–ї–µ–Љ –Р—Е–Љ–µ–і –Р–ї—М-–Ъ–∞–∞–±—Ц–∞–љ–≥–ї. Salem Ahmed Salem Al-Kaabi –Э–∞—А–Њ–і–Є–≤—Б—П –Ю–Р–Х–У—А–Њ–Љ–∞–і—П–љ—Б—В–≤–Њ –Ю–Р–Х–Ф—Ц—П–ї—М–љ—Ц—Б—В—М –Ф–Є–њ–ї–Њ–Љ–∞—В–Я–Њ—Б–∞–і–∞ –Э–∞–і–Ј–≤–Є—З–∞–є–љ–Є–є —Ц –Я–Њ–≤–љ–Њ–≤–∞–ґ–љ–Є–є –Я–Њ—Б–Њ–ї –Ю–Р–Х –≤ –£–Ї—А–∞—Ч–љ—Ц–Ґ–µ—А–Љ—Ц–љ –Ј 2017–Я–Њ–њ–µ—А–µ–і–љ–Є–Ї –Р–±–і—Г–ї—Б–∞–ї—П–Љ –•–∞—А–µ–± –Ю–±–∞–є–і –Р–ї—М-–†—Г–Љ–µ–є—Б—Ц –°–∞–ї–µ–Љ –Р—Е–Љ–µ–і –Р–ї—М-–Ъ–∞–∞–±—Ц (–∞–љ–≥–ї. Salem Ahmed Salem Al-Kaabi) вАФ –µ–Љ—Ц—А–∞—В—Б—М–Ї–Є–є –і–Є–њ...

34th General Assembly of NewfoundlandConfederation Building East Block. Seat of the Newfoundland and Labrador government and the House of Assembly from 1960 to present.HistoryFoundedNovember 30, 1966 (1966-11-30)DisbandedOctober 4, 1971 (1971-10-04)Preceded by33rd General Assembly of NewfoundlandSucceeded by35th General Assembly of NewfoundlandLeadershipPremierJoey Smallwood ElectionsLast election1966 Newfoundland general election The members of the 34t...

F.4 Buzzard Martinsyde Buzzard in the Aviation Museum of Finland Role Biplane fighterType of aircraft Manufacturer Martinsyde Designer George Handasyde First flight June 1918 Retired 1940, by Finland[1] Primary users Royal Air ForceSoviet Air Force Number built ~370[2] The Martinsyde F.4 Buzzard was developed as a powerful and fast biplane fighter for the Royal Air Force (RAF), but the end of the First World War led to the abandonment of large-scale production. Fewer than...

On closed convex subsets in Hilbert space This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Hilbert projection theorem вАУ news ¬Ј newspapers ¬Ј books ¬Ј scholar ¬Ј JSTOR (February 2020) In mathematics, the Hilbert projection theorem is a famous result of convex analysis that says that for every vector x {...

Iron Age hillfort in Wiltshire, England Knook CastleShown within WiltshireLocationWiltshireRegionSouthern EnglandCoordinates51¬∞11вА≤43вА≥N 2¬∞03вА≤31вА≥W / 51.1954¬∞N 2.0585¬∞W / 51.1954; -2.0585Typesub-rectangular univallate hillfortArea1.75 hectares (4.3 acres)HistoryMaterialChalkPeriodsIron AgeSite notesArchaeologistsSir Richard Colt Hoare,William Cunnington,Petrie,GrinsellPublic accessfootpaths Knook Castle is the site of an Iron Age univallate hillfort on Kn...

Dinas PsikologiTentara Nasional Indonesia Angkatan DaratLambang TNI Angkatan DaratDibentuk15 Juni 1950Negara IndonesiaCabang TNI Angkatan DaratBagian dariTentara Nasional IndonesiaMotoUpakriya Labdha Prayojana BallotamaSitus webwww.dispsiad.mil.idTokohKomandan saat iniBrigjend TNI Henny Setyono, S.Psi., M.Si. Dinas Psikologi TNI Angkatan Darat (atau Dispsiad) di lingkungan TNI AD merupakan kelanjutan dari Leger Psychologiesche Dienst (LPD, Dinas Psikologi Tentara KNIL -red). Biasa disebu...

American educator and writer Cindy LovellBornCindy Louise Pletcher (1956-05-06) May 6, 1956 (age 67)Altoona, Pennsylvania, U.S.Alma materStetson University (BA, MA) and The University of Iowa (Ph.D.)Occupation(s)Educator, WriterEmployerEpic Flight AcademyKnown forEducation, Writing, Mark TwainNotable workMark Twain: Words & Music, Orthophonic Joy: The 1927 Bristol Sessions Revisited, and Linguistics for K-12 Classroom ApplicationAwards2010 Hannibal NAACP Martin Luther King,...

KakaoMusicDeveloper(s)KakaoInitial release2013Operating systemiOS, AndroidAvailable inKoreanTypemusic streamingWebsiteOfficial website KakaoMusic (Hangul: мєімєімШ§лЃ§мІБ) was a music streaming service launched by Kakao. It lets users stream and buy music while also allowing them to share songs and connect with friends through KakaoTalk. In 2017, Kakao merged Kakao Music into Melon, the companyвАЩs other music streaming service.[1][2] Features People can create their own music...
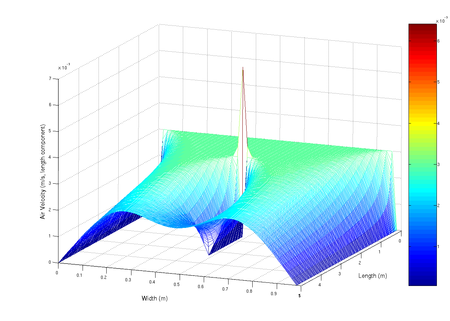
Persamaan diferensial adalah persamaan matematika untuk fungsi satu variabel atau lebih, yang menghubungkan nilai fungsi itu sendiri dan turunannya dalam berbagai orde. Persamaan diferensial memegang peranan penting dalam rekayasa, fisika, ilmu ekonomi dan berbagai macam disiplin ilmu lain. Visualisasi aliran udara ke dalam saluran dimodelkan sesuai persamaan Navier-Stokes Persamaan diferensial muncul dalam berbagai bidang sains dan teknologi, bilamana hubungan deterministik yang melibatkan b...

For the New Zealand Maori community leader, born Ripeka Matene (1882вАУ1953), see Ripeka Wharawhara Love. This biography of a living person includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately, especially if potentially libelous or harmful. Please help to improve this article by introducing more precise citati...
