Prado
|
Read other articles:

El beso de Gustavo Adolfo BécquerGénero narraciónTema(s) leyendaAmbientada en Toledo Idioma EspañolPaís EspañaFecha de publicación 1863[editar datos en Wikidata] El beso es una de las Leyendas de Gustavo Adolfo Bécquer, ambientada en Toledo. Se publicó en por primera vez en la revista La América el 27 de julio de 1863. Relación con otras obras Obras de Bécquer, t. II, 4ª ed., 1885, en DjVu. Esta trágica leyenda está relacionada con la rima LXXVI del mismo autor.[...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (نوفمبر 2018) روبن كولمان معلومات شخصية الميلاد 30 مارس 1973 (50 سنة) فريندزوود مواطنة الولايات المتحدة لون الشعر شعر أشقر عضوة في ساج أفترا، ونقابة ممثلي...

Der von Johansdorf im Codex Manesse Albrecht von Johansdorf (auch Albertus de Janestorf, Albert von Jahenstorf oder Der von Johansdorf, * vor 1180; † nach 1209) war ein Minnesänger. Er ist vor allem für seine Kreuzzugslyrik bekannt. Inhaltsverzeichnis 1 Leben 2 Werk 2.1 Lieder 2.2 Liedbeispiel 3 Werke 4 Literatur 5 Weblinks 6 Einzelnachweise Leben In den Jahren 1172 bis 1255 findet man den Namen Johansdorf in verschiedenen Schreibweisen insgesamt dreizehnmal in Dokumenten. Drei Generation...

Муасір Родрігес Сантус Особисті дані Повне ім'я Моачир Родригуес дос Сантос Народження 21 березня 1970(1970-03-21) (53 роки) Белу-Оризонті, Бразилія Зріст 185 см Вага 84 кг Громадянство Бразилія Позиція півзахисник Інформація про клуб Поточний клуб завершив кар'єру Проф�...

In the run up to the next Ukrainian parliamentary election, various organisations carried out opinion polling to gauge voter intention in Ukraine. The results of the polls are displayed in this article. The date range for these opinion polls are from the 2019 Ukrainian parliamentary election, held on 21 July, to the day of the next election. Due to ongoing martial law in Ukraine, opinion polling seems banned.[citation needed] Trusted polling firms In Ukraine, there are many unknown an...

La asamblea se realizaba en Gamla Uppsala.El Thing de todos los suecos (allra Svía þing,[1] Þing allra Svía,[2] o Disaþing,[3] Kyndilþing[4]) fue la asamblea general que se sostuvo desde tiempos prehistóricos hasta la Edad Media, a finales de febrero o principios de marzo en Gamla Uppsala, Suecia.[5] Junto a esta reunión también se realizaba una gran feria y una celebración pagana llamada Dísablót.[4][6] Según la Ley de Uppland, en...

Village in Kuyavian-Pomeranian Voivodeship, PolandWolwarkVillageWolwarkCoordinates: 52°59′N 17°42′E / 52.983°N 17.700°E / 52.983; 17.700Country PolandVoivodeshipKuyavian-PomeranianCountyNakłoGminaSzubinPopulation289Websitehttp://www.wolwark.republika.pl Wolwark [ˈvɔlvark] is a village in the administrative district of Gmina Szubin, within Nakło County, Kuyavian-Pomeranian Voivodeship, in north-central Poland.[1] It lies approximately 5 kilometr...

Filipino basketball player (born 1993) In this Philippine name, the middle name or maternal family name is Carreon and the surname or paternal family name is Thompson. Scottie ThompsonThompson with the Barangay Ginebra San Miguel in 2021No. 9 – Barangay Ginebra San MiguelPositionShooting guard / Point guardLeaguePBAPersonal informationBorn (1993-07-12) July 12, 1993 (age 30)Padada, Davao del Sur, PhilippinesNationalityFilipinoListed height6 ft 1 in (1.85 ...

Ляймен Leimen — місто — Вид Ляймен Герб Координати: 49°20′53″ пн. ш. 08°41′28″ сх. д. / 49.34806° пн. ш. 8.69111° сх. д. / 49.34806; 8.69111 Країна Німеччина Земля Баден-Вюртемберг Округ Карлсруе Район Рейн-Неккар Площа - Повна 20,64 км² Ви�...

Abe MostBackground informationBirth nameAbraham MostBorn(1920-02-27)February 27, 1920New York CityDiedOctober 10, 2002(2002-10-10) (aged 82)Los AngelesGenresJazz, swingOccupation(s)MusicianInstrument(s)ClarinetYears active1930s–1980sMusical artist Abe Most (February 27, 1920 – October 10, 2002) was a swing clarinetist and alto saxophonist who is known for his performances and recordings of the works of Artie Shaw and Benny Goodman. He began his career in 1939 as a member of Les Brown...

UK TV channel owned by UKTV This article is about the British television channel. For the channel formerly known as UKTV Drama, see Alibi (TV channel). Television channel DramaLogo used since 8 July 2013.CountryUnited Kingdom and IrelandBroadcast areaUnited Kingdom and IrelandProgrammingLanguage(s)EnglishPicture format1080i HDTV(SDTV feed downscaled to 16:9 576i)Timeshift serviceDrama +1OwnershipOwnerBBC StudiosParentUKTVSister channelsAlibiDaveEdenGoldWYesterdayHistoryLaunched8 July 201...

Vermindering van het oppervlak van de Dode Zee Het geplande tracé van het Rode-Zee-Dode-Zeekanaal in het rood Het Dode Zeekanaal, ook wel het Rode Zee-Dode Zeekanaal genoemd, was een geplande, circa 180-200 km lange pijpleiding door Jordanië die een verbinding zou vormen tussen de Rode Zee bij de kustplaats Akaba en de Dode Zee. In 2021 is het in 2017 al opgeschorte project door Jordanië afgelast.[1] Het doel van het project is meerledig. Ten eerste zullen Jordanië, Israël en de ...

Hengan International Group Company LimitedNative name恆安國際集團有限公司Romanized nameHéng'ān Guójì Jítuán YǒuxiàngōngsīTypePrivately owned companyTraded asSEHK: 1044Hang Seng Index componentIndustryHygiene productsFounded1985; 38 years ago (1985)HeadquartersJinjiang, Fujian, People's Republic of ChinaArea servedChinaKey peopleChairman: Sze Man BokDeputy chairman and CEO: Hui Lin ChitProductssanitary napkins, baby diapers, adult diapersWebsitewww.he...

American glamour model and actress Deanna BrooksDeanna Brooks, Los Angeles, California on November 29, 2011Playboy centerfold appearanceMay 1998Preceded byHolly Joan HartSucceeded byMaria Luisa GilPersonal detailsBorn (1974-04-30) April 30, 1974 (age 49)Boulder City, Nevada[1]Height5 ft 4.5 in (1.64 m)[1] Deanna Brooks (born Deanna Wilson[2] on April 30, 1974, in Boulder City, Nevada)[1] is an American glamour model and actress who was Playb...

Award ceremony for performances of 2010 17th Screen Actors Guild AwardsAwarded forOutstanding motion picture and primetime television performancesDateJanuary 30, 2011 (2011-01-30)LocationShrine AuditoriumLos Angeles, CaliforniaCountryUnited StatesPresented byScreen Actors GuildFirst awarded1995Websitewww.sagawards.orgTelevision/radio coverageNetworkTNT and TBSsimultaneous broadcast ← 16th · Screen Actors Guild Awards · 18th → The 17th Annual Sc...

American social psychologist (born 1933) Philip ZimbardoZimbardo in 2017BornPhilip George Zimbardo (1933-03-23) March 23, 1933 (age 90)New York City, New York, U.S.NationalityAmericanAlma materBrooklyn College (BA)Yale University (MS, PhD)Known forStanford prison experimentThe Time paradoxThe Lucifer EffectAbu Ghraib prison analysistime perspective therapysocial intensity syndromeSpouses Rose Abdelnour (m. 1957; div. 1971) Chr...

Main article: 1952 United States presidential election 1952 United States presidential election in North Carolina ← 1948 November 4, 1952[1] 1956 → All 14 North Carolina votes to the Electoral College Nominee Adlai Stevenson Dwight D. Eisenhower Party Democratic Republican Home state Illinois New York[2] Running mate John Sparkman Richard Nixon Electoral vote 14 0 Popular vote 652,803 558,107 Percentage 53.91% 46.09% County resu...

Painting by Bronzino Allegory of Happiness (1567) by Bronzino Allegory of Happiness is an oil on copper painting by Bronzino, probably first produced for the Studiolo of Francesco I, signed BROZ. FAC. and now in the Uffizi in Florence.[1][2][3][4] It is now in a fluted and gilded 17th century wooden frame.[5] Most art historians date it to around 1567, and it is first mentioned in the Uffizi inventory in 1635/8.[6][7] Iconography Happine...

Traditional song Wikisource has original text related to this article: Child's Ballads/49 The Twa Brothers from The Book of British Ballads (1842) The Twa Brothers is a traditional ballad (Roud 38, Child 49) existing in many variants.[1] Synopsis Two brothers are wrestling when a blade that one of them is carrying mortally wounds the other; occasionally, one of them stabs the other intentionally. Attempts to staunch the blood are not successful, and the dying brother tells the living ...
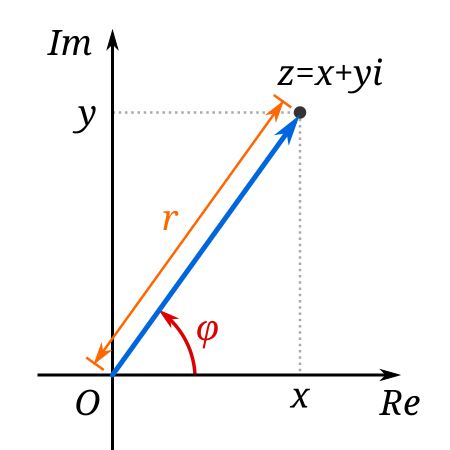
Un număr complex poate fi reprezentat vizual ca pereche de numere (a, b) formând un vector de poziție al unui punct în diagrama Argand, reprezentând planul complex. Re e axa reală, Im e axa imaginară, i e unitatea imaginară care îndeplinește i2 = −1. În matematică, numerele complexe sunt numere introduse ca soluții ale ecuațiilor de forma x 2 + p = 0 , {\displaystyle x^{2}+p=0,} cu p număr real strict pozitiv. Formal, corpul numerelor complexe, notat cu C {\displaystyle \ma...
