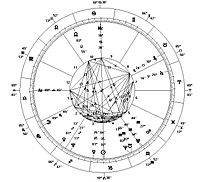
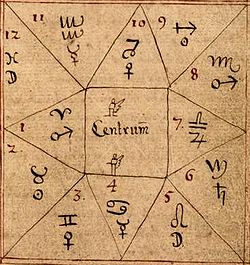
하우스 (점성술)
|
Read other articles:

Family of termites Rhinotermitidae Reticulitermes banyulensis Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Blattodea Infraorder: Isoptera Nanorder: Neoisoptera Family: RhinotermitidaeFroggatt, 1897 Subfamilies See text Rhinotermitidae is a family of wood-soil interface feeding termites commonly known as the Subterranean termites. Many members of this family are known pests that can cause extensive damage to buildings or other wooden st...

Television channel TLCCountryIndiaBroadcast areaIndian SubcontinentHeadquartersMumbai, Maharashtra, IndiaProgrammingLanguage(s)EnglishHindiPicture format1080i HDTV(downscaled to 576i for the SD feed)OwnershipOwnerWarner Bros. Discovery IndiaSister channelsSee List of channels owned by Warner Bros. Discovery in IndiaHistoryLaunchedOctober 2004 (2004-10)Former namesDiscovery Travel & Living (2004-2010)LinksWebsiteTLC IndiaAvailability - Available on all major Indian DTH & Cabl...
Die Liste der Kulturdenkmale in Blasewitz umfasst sämtliche Kulturdenkmale der Dresdner Gemarkung Blasewitz. Große Teile der Gemarkung (Ausnahmen sind Neugruna und kleinere Randgebiete) liegen im Denkmalschutzgebiet Blasewitz/Striesen-Nordost (in Kraft gesetzt am 28. März 1997).[1] Die Anmerkungen sind zu beachten. Aufgrund der hohen Anzahl der Kulturdenkmale wurde die alphabetisch nach Adressen geordnete Liste in folgende zwei Teillisten untergliedert: Liste der Kulturdenkmale in ...

Raven Riley Información personalNombre de nacimiento Sarah Frances Pate[1]Nacimiento 6 de septiembre de 1986 (37 años)Heaven, Arizona,Estados UnidosNacionalidad EstadounidenseLengua materna Inglés Características físicasAltura 1,63 m (5′ 4″)Peso 53 kg (117 lb)Medidas 35-24-36Ojos CastañosCabello CastañoPecho natural SíInformación profesionalOcupación Modelo, actriz pornográfica y modelo erótica Años activa 2006-2007Películas 3 (IAFD)Sitio web www.ravenr...

American sitcom (2005–2014) How I Met Your MotherThe cast pictured in the opening sequenceGenre Sitcom Romantic comedy Comedy drama Created by Carter Bays Craig Thomas Starring Josh Radnor Jason Segel Cobie Smulders Neil Patrick Harris Alyson Hannigan Cristin Milioti Narrated byBob SagetOpening themeHey, Beautiful by The SolidsComposerJohn SwihartCountry of originUnited StatesOriginal languageEnglishNo. of seasons9No. of episodes208 (list of episodes)ProductionExecutive producers Carter Bay...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Patut Sudarsono – berita · surat kabar · buku · cendekiawan · JSTOR Patut SudarsonoInformasi pribadiLahir4 Maret 1961 (umur 62) Purwodadi, Jawa TengahAlma materAkademi Militer (1984)Karier militerPihak&#...

جزء من سلسلة مقالات حولالإسلام حسب البلد الإسلام في إفريقيا أنغولا بنين بوتسوانا بوركينا فاسو بوروندي الكاميرون الرأس الأخضر أفريقيا الوسطى نشاد الجزائر جزر القمر الكونغو الديمقراطية الكونغو ساحل العاج جيبوتي مصر غينيا الاستوائية إريتريا إثيوبيا الغابون غامبيا غانا غي...

1983 novel by Philip José Farmer Gods of Riverworld Cover by Don PunchatzAuthorPhilip José FarmerCountryUnited StatesLanguageEnglishSeriesRiverworldGenreScience fictionPublisherPutnam Publishing GroupPublication date1983Media typePrint (Hardcover & Paperback)ISBN0-399-12843-3OCLC9533068Dewey Decimal813/.54 19LC ClassPS3556.A72 G6 1983Preceded byThe Magic Labyrinth Gods of Riverworld (1983) is a science fiction novel by American writer Philip José Farmer, the fifth ...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Diving at the 2016 Summer Olympics – Men's 3 metre springboard – news · newspapers · books · scholar · JSTOR (August 2016) (Learn how and when to remove this template message) Men's 3 metre springboardat the Games of the XXXI OlympiadVenueMaria Lenk Aquatic CenterDate15–16 A...

Brazilian footballer In this Portuguese name, the first or maternal family name is de Almeida and the second or paternal family name is Monteiro. Felipe Felipe with Atlético Madrid in 2019Personal informationFull name Felipe Augusto de Almeida Monteiro[1]Date of birth (1989-05-16) 16 May 1989 (age 34)Place of birth São Paulo, BrazilHeight 1.90 m (6 ft 3 in)[2]Position(s) Centre-backTeam informationCurrent team Nottingham ForestNumber 18Youth career200...

Australian TV series or program Half a World AwayTelevision miniseries posterGenreAdventureBased onHalf a World Away (story)by Ross DimseyWritten byMichael BrindleyScreenplay byPeter Hepworth (treatment)Directed byMarcus ColeStarring Helen Slater Barry Bostwick Robert Reynolds Caroline Goodall Tim Hughes Theme music composerPeter SullivanCountry of originAustraliaOriginal languageEnglishNo. of episodes2 x 2 hoursProductionProducerRoss DimseyCinematographyChris DavisEditorKen TylerRunning...

1964 film Il magnifico cornutoDirected byAntonio PietrangeliWritten byDiego Fabbri, Ruggero MaccariCinematographyArmando NannuzziEdited byEraldo Da RomaMusic byArmando TrovajoliRelease date1964Running time124 minutesCountryItalyLanguageItalian The Magnificent Cuckold or Il magnifico cornuto is a 1964 Italian sex comedy film directed by Antonio Pietrangeli and based on the Belgian play Le Cocu magnifique written by Fernand Crommelynck. Plot The Magnificent Cuckold is about a hat tycoon who is ...

Cet article est une ébauche concernant une localité néo-zélandaise. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. WaipukurauGéographiePays Nouvelle-ZélandeRégion Hawke's BayDistrict District de Central Hawke's BayCoordonnées 39° 59′ 42″ S, 176° 33′ 25″ EDémographiePopulation 4 610 hab. (2020)modifier - modifier le code - modifier Wikidata Waipukura...

Pour les articles homonymes, voir Ligne M1. Cet article est une ébauche concernant la Roumanie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. M1 Station Piața Unirii 1 commune aux lignes M1 et M3, en 2012 Réseau Métro de Bucarest Histoire Mise en service 16 novembre 1979 Dernière extension 1990 Exploitant Metrorex Exploitation Points d’arrêt 22 Longueur 31.7 km Jours de fonctionnement L, Ma,&#...

For other CJM schools, see Convent of Jesus and Mary. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Convent of Jesus and Mary, Lahore – news · newspapers · books · scholar · JSTOR (May 2021) (Learn how and when to remove this template message) Private primary and secondary school in PakistanConvent of Jesu...

American cyclist (1883–1904) George LeanderPersonal informationBorn(1883-05-12)12 May 1883Chicago, United StatesDied23 August 1904(1904-08-23) (aged 21)Paris, FranceSportSportTrack cycling George Leander (12 May 1883 – 23 August 1904) was an American track cyclist. He became professional in 1902. Leander was one of the first generation of six-day cyclists. He won the Six Days of New York in 1902 at Madison Square Garden together with Floyd Krebs. He finished second a year later with ...

Carlos Eugénio Correia da SilvaCvTE GCA ComCPortrait, c. 1890Governor of MacauIn office1876–1879Preceded byJosé Maria Lobo de ÁvilaSucceeded byJoaquim José da GraçaGovernor-general of MozambiqueIn office1881–1882Preceded byAugusto César Rodrigues SarmentoSucceeded byJosé de Almeida d'ÁvilaGovernor of Portuguese IndiaIn office1882–1886Preceded byCaetano Alexandre de Almeida e AlbuquerqueSucceeded byGovernment Council of the State of India Personal detailsBorn(1834-12-17)17 Decemb...

Chaopha Swargadeo of Ahom Kingdom SunyatphaaChaopha Swargadeo of Ahom KingdomAhom KingReign1670 CE to 1672 CEPredecessorSupangmungSuccessorSuklamphaaBornMaju GohainAhom kingdomDiedc. 1672Charaideo, Ahom kingdomNamesSwargadeo Udayaditya SinghaHouseCharingiaDynastyAhom dynastyFatherNamrupia RajaReligionAhom religion Hinduism Ahom dynasty List of Ahom kings 1 Sukaphaa 1228–1268 2 Suteuphaa 1268–1281 3 Subinphaa 1281–1293 4 Sukhaangphaa 1293–1332 5 Sukhrangpha 1332&#...

Dutch fashion model Doutzen KroesKroes in 2015Born (1985-01-23) 23 January 1985 (age 38)Gytsjerk, Friesland, NetherlandsOccupationsModelactressphilanthropistYears active2003–presentSpouse Sunnery James Gorré (m. 2010)Children2Modeling informationHeight1.79 m (5 ft 10+1⁄2 in)[1]Hair colorBlondeEye colorBlueAgencyDNA Models (New York)[1] Doutzen Kroes (West Frisian: [ˈdɔu̯tsə(ŋ) ˈkrus], Dutch: [ˈ...

1963 film by K. S. Gopalakrishnan For other uses, see Karpagam (disambiguation). KarpagamPosterDirected byK. S. GopalakrishnanWritten byK. S. GopalakrishnanProduced byK. S. SabarinathanStarringSee CastCinematographyM. KarnanEdited byR. DevarajanMusic byViswanathan–RamamoorthyProductioncompanyAmar Jothi MoviesRelease date 15 November 1963 (1963-11-15) Running time162 minutes[1]CountryIndiaLanguageTamil Karpagam is a 1963 Indian Tamil-language drama film written and dir...