![]() н•©м„ұкіұ, мғҒнҳёмғҒкҙҖ, мһҗкё°мғҒкҙҖмқҳ 비көҗ.
н•©м„ұкіұ, мғҒнҳёмғҒкҙҖ, мһҗкё°мғҒкҙҖмқҳ 비көҗ.
н•©м„ұкіұ(еҗҲжҲҗ-), лҳҗлҠ” мҪҳлІҢлЈЁм…ҳ(convolution)мқҖ н•ҳлӮҳмқҳ н•ЁмҲҳмҷҖ лҳҗ лӢӨлҘё н•ЁмҲҳлҘј л°ҳм „ мқҙлҸҷн•ң к°’мқ„ кіұн•ң лӢӨмқҢ, кө¬к°„м—җ лҢҖн•ҙ м Ғ분н•ҳм—¬ мғҲлЎңмҡҙ н•ЁмҲҳлҘј кө¬н•ҳлҠ” мҲҳн•ҷ м—°мӮ°мһҗмқҙлӢӨ.
м •мқҳ
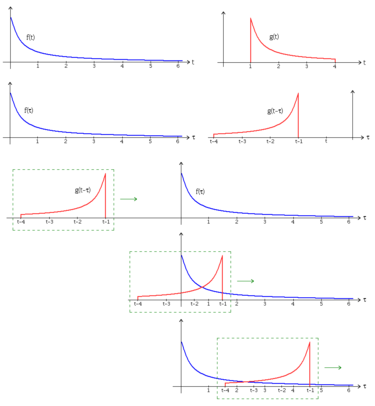 н•©м„ұкіұ м—°мӮ°мқ„ м„ӨлӘ…н•ҳлҠ” к·ёлһҳн”„ лЁјм Җ мһ„мқҳмқҳ ліҖмҲҳ(dummy variable)лҘј м •мқҳн•ңлӢӨ. (мқҙ кІҪмҡ°м—җлҠ”
н•©м„ұкіұ м—°мӮ°мқ„ м„ӨлӘ…н•ҳлҠ” к·ёлһҳн”„ лЁјм Җ мһ„мқҳмқҳ ліҖмҲҳ(dummy variable)лҘј м •мқҳн•ңлӢӨ. (мқҙ кІҪмҡ°м—җлҠ”  лҘј м •мқҳн•Ё) мқҙм ң м •мқҳн•ң ліҖмҲҳлҘј 축мңјлЎң л‘җ н•ЁмҲҳмқҳ нҢҢнҳ•мқ„ к·ёлҰ°лӢӨ. к·ё лӢӨмқҢмңјлЎң л‘җ н•ЁмҲҳ мӨ‘ н•ҳлӮҳлҘј м„ нғқн•ҙ
лҘј м •мқҳн•Ё) мқҙм ң м •мқҳн•ң ліҖмҲҳлҘј 축мңјлЎң л‘җ н•ЁмҲҳмқҳ нҢҢнҳ•мқ„ к·ёлҰ°лӢӨ. к·ё лӢӨмқҢмңјлЎң л‘җ н•ЁмҲҳ мӨ‘ н•ҳлӮҳлҘј м„ нғқн•ҙ  축м—җ лҢҖн•ҙ л°ҳм „(time-invert)н•ҳкі tлҘј лҚ”н•ңлӢӨ. (м–ҙл–Ө н•ЁмҲҳлҘј м„ нғқн•ҳл“ м§Җ кҙҖкі„ м—ҶлӢӨ.) л°©кёҲ м„ нғқн•ң н•ЁмҲҳлҠ”
축м—җ лҢҖн•ҙ л°ҳм „(time-invert)н•ҳкі tлҘј лҚ”н•ңлӢӨ. (м–ҙл–Ө н•ЁмҲҳлҘј м„ нғқн•ҳл“ м§Җ кҙҖкі„ м—ҶлӢӨ.) л°©кёҲ м„ нғқн•ң н•ЁмҲҳлҠ”  -축м—җ лҢҖн•ҙ м•һл’ӨлЎң мӣҖм§Ғмқј мҲҳ мһҲлӢӨ. мқҙл•Ң t ліҖмҲҳмқҳ к°’мқҙ ліҖнҷ”н•ҳм§Җл§Ң мң„ к·ёлҰјм—җм„ң нҢҢнҳ•мқҳ лҫ°мЎұн•ң л¶Җ분мқҖ н•ӯмғҒ t-1м—җ мң„м№ҳн•ҙ мһҲлӢӨ. мқҙм ңлҠ” мқҢмқҳ л¬ҙн•ңлҢҖм—җм„ңл¶Җн„° м–‘мқҳ л¬ҙн•ңлҢҖк№Ңм§Җ м„ нғқн•ң н•ЁмҲҳлҘј мқҙлҸҷмӢңнӮӨл©ҙм„ң л‘җ н•ЁмҲҳмқҳ кіұмқҳ м Ғ분 к°’мқ„ м°ҫлҠ”лӢӨ. мқҙ кІ°кіјлҘј нҢҢнҳ•мңјлЎң н‘ңмӢңн•ң кІғмқҙ л°”лЎң л‘җ н•ЁмҲҳмқҳ н•©м„ұкіұмқҙлӢӨ. (мң„ к·ёлҰјм—җлҠ” н‘ңмӢңн•ҳм§Җ м•Ҡм•ҳлӢӨ.)
-축м—җ лҢҖн•ҙ м•һл’ӨлЎң мӣҖм§Ғмқј мҲҳ мһҲлӢӨ. мқҙл•Ң t ліҖмҲҳмқҳ к°’мқҙ ліҖнҷ”н•ҳм§Җл§Ң мң„ к·ёлҰјм—җм„ң нҢҢнҳ•мқҳ лҫ°мЎұн•ң л¶Җ분мқҖ н•ӯмғҒ t-1м—җ мң„м№ҳн•ҙ мһҲлӢӨ. мқҙм ңлҠ” мқҢмқҳ л¬ҙн•ңлҢҖм—җм„ңл¶Җн„° м–‘мқҳ л¬ҙн•ңлҢҖк№Ңм§Җ м„ нғқн•ң н•ЁмҲҳлҘј мқҙлҸҷмӢңнӮӨл©ҙм„ң л‘җ н•ЁмҲҳмқҳ кіұмқҳ м Ғ분 к°’мқ„ м°ҫлҠ”лӢӨ. мқҙ кІ°кіјлҘј нҢҢнҳ•мңјлЎң н‘ңмӢңн•ң кІғмқҙ л°”лЎң л‘җ н•ЁмҲҳмқҳ н•©м„ұкіұмқҙлӢӨ. (мң„ к·ёлҰјм—җлҠ” н‘ңмӢңн•ҳм§Җ м•Ҡм•ҳлӢӨ.)
л‘җ к°ңмқҳ н•ЁмҲҳ  мҷҖ
мҷҖ  к°Җ мһҲмқ„ л•Ң, л‘җ н•ЁмҲҳмқҳ н•©м„ұкіұмқ„ мҲҳн•ҷ кё°нҳёлЎңлҠ”
к°Җ мһҲмқ„ л•Ң, л‘җ н•ЁмҲҳмқҳ н•©м„ұкіұмқ„ мҲҳн•ҷ кё°нҳёлЎңлҠ”  мҷҖ к°ҷмқҙ н‘ңмӢңн•ңлӢӨ.
мҷҖ к°ҷмқҙ н‘ңмӢңн•ңлӢӨ.
н•©м„ұкіұ м—°мӮ°мқҖ л‘җ н•ЁмҲҳ f, g к°ҖмҡҙлҚ° н•ҳлӮҳмқҳ н•ЁмҲҳлҘј л°ҳм „(reverse), м „мқҙ(shift)мӢңнӮЁ лӢӨмқҢ,
лӢӨлҘё н•ҳлӮҳмқҳ н•ЁмҲҳмҷҖ кіұн•ң кІ°кіјлҘј м Ғ분н•ҳлҠ” кІғмқ„ мқҳлҜён•ңлӢӨ.
мқҙлҘј мҲҳн•ҷ кё°нҳёлЎң н‘ңмӢңн•ҳл©ҙ лӢӨмқҢкіј к°ҷлӢӨ.

лҳҗн•ң g н•ЁмҲҳ лҢҖмӢ м—җ f н•ЁмҲҳлҘј л°ҳм „, м „мқҙ мӢңнӮӨлҠ” кІҪмҡ° лӢӨмқҢкіј к°ҷмқҙ н‘ңмӢңн• мҲҳлҸ„ мһҲлӢӨ. мқҙ л‘җ м—°мӮ°мқҖ нҳ•нғңлҠ” лӢӨлҘҙм§Җл§Ң к°ҷмқҖ кІ°кіјк°’мқ„ к°–лҠ”лӢӨ.

мң„мқҳ м Ғ분м—җм„ң м Ғ분 кө¬к°„мқҖ н•ЁмҲҳ fмҷҖ gк°Җ м •мқҳлҗң лІ”мң„м—җ л”°лқјм„ң лӢ¬лқјм§„лӢӨ.
лҳҗн•ң л‘җ нҷ•лҘ ліҖмҲҳ XмҷҖ Yк°Җ мһҲмқ„ л•Ң к°Ғк°Ғмқҳ нҷ•лҘ л°ҖлҸ„ н•ЁмҲҳлҘј fмҷҖ gлқјкі н•ҳл©ҙ, XмҷҖ Yк°Җ м„ңлЎң лҸ…лҰҪмқҙлқјлҠ” к°Җм • н•ҳм—җ, X+Yмқҳ нҷ•лҘ л°ҖлҸ„ н•ЁмҲҳлҠ”  лЎң н‘ңмӢңн• мҲҳ мһҲлӢӨ.
лЎң н‘ңмӢңн• мҲҳ мһҲлӢӨ.
мқҙмӮ° н•©м„ұкіұ
мқҙмӮ° н•ЁмҲҳмқҳ кІҪмҡ°, н•©м„ұкіұмқ„ лӢӨмқҢкіј к°ҷмқҙ м •мқҳ н•ңлӢӨ.

л‘җк°ңмқҳ лӢӨн•ӯмӢқмқ„ кіұн•ң кІ°кіјмӢқмқҳ кі„мҲҳлҠ” мӣҗлһҳ лӢӨн•ӯмӢқмқҳ кі„мҲҳл“Өмқҳ н•©м„ұкіұмңјлЎң лӮҳнғҖлӮј мҲҳ мһҲлӢӨ.
нҠ№м„ұ
н•©м„ұкіұмқҖ лӢӨмқҢкіј к°ҷмқҖ м„ұм§Ҳл“Өмқ„ л§ҢмЎұмӢңнӮЁлӢӨ.
көҗнҷҳ лІ•м№ҷ

кІ°н•© лІ•м№ҷ

분배 лІ•м№ҷ

мҠӨм№јлқј кіұмқҳ кІ°н•© лІ•м№ҷ
мӢӨмҲҳ нҳ№мқҖ ліөмҶҢмҲҳ к°’ aм—җ лҢҖн•ҙм„ң

лҜёл¶„ лІ•м№ҷ

 лҠ” н•ЁмҲҳ fмқҳ лҜёл¶„ к°’мқ„ лӮҳнғҖлӮёлӢӨ.
лҳҗлҠ” мқҙмӮ° н•ЁмҲҳм—җм„ң лҜёл¶„ м—°мӮ°мһҗ
лҠ” н•ЁмҲҳ fмқҳ лҜёл¶„ к°’мқ„ лӮҳнғҖлӮёлӢӨ.
лҳҗлҠ” мқҙмӮ° н•ЁмҲҳм—җм„ң лҜёл¶„ м—°мӮ°мһҗ лҘј лӮҳнғҖлӮёлӢӨ.
лҘј лӮҳнғҖлӮёлӢӨ.
к°ҷмқҙ ліҙкё°