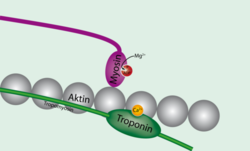
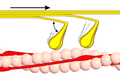
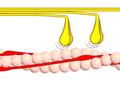
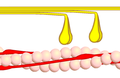
근수축
|
Read other articles:

Haakon V de Noruega Sello de Haakon IV.Información personalNacimiento 10 de abril de 1270 Tønsberg (Noruega) Fallecimiento 8 de mayo de 1319 (49 años)Tønsberg (Noruega) Sepultura St Mary's Church Nacionalidad NoruegaFamiliaFamilia Hårfagreætta Padres Magnus VI de Noruega Ingeborg Eriksdatter Cónyuge Isabelle de JoignyEufemia de Arnstein (desde 1299) Hijos Ingeborg of Norway Información profesionalCargos ocupados Monarca de Noruega (1299-1319) Escudo SEGRETVM HAQVINI DEI GRA ...

Italian racecar driver Max AngelelliAngelelli at the New Jersey Motorsports Park in 2008Born (1966-12-15) 15 December 1966 (age 56)Bologna, ItalyRacing licence FIA BronzeNationality Italian24 Hours of Le Mans careerYears1994, 1999–2002Best finish9th (2002) 2011 Daytona Prototype with Ricky Taylor Massimiliano Angelelli (born 15 December 1966) is a retired Italian racecar driver.[1] He won the 2005 and 2017 24 Hours of Daytona and the 2001 Six Hours at the Glen. Also he was...

селище Богородицьке Богородицкое Країна Росія Суб'єкт Російської Федерації Воронезька область Муніципальний район Панінський район Поселення Дмитриевське сільське поселення Код ЗКАТУ: 20235806002 Код ЗКТМО: 20635406106 Основні дані Населення ▼ 35 (2010)[1] Поштовий індекс 3961...

Gräpel Gemeinde Estorf Wappen von Gräpel Koordinaten: 53° 34′ N, 9° 11′ O53.56778929.183069Koordinaten: 53° 34′ 4″ N, 9° 10′ 59″ O Einwohner: 664 (1. Jan. 2012) Eingemeindung: 1. Juli 1972 Postleitzahl: 21727 Vorwahl: 04140 Gräpel (Niedersachsen) Lage von Gräpel in Niedersachsen Blick von Westen 2013Blick von Westen 2013 Gräpel (niederdeutsch Gröpel) ist ein Ortsteil der Gemeinde Estorf im Landkreis Stade i...

Điện cơ Thống nhấtTập tin:Logo of vinawind.jpgLoại hìnhSản xuất đồ điệnLĩnh vực hoạt độngĐiện cơ, động cơ điệnThành lập27 tháng 3 năm 1964; 59 năm trước (1964-03-27)Người sáng lậpTập thểTrụ sở chính164 Nguyễn Đức Cảnh, Tương Mai, Hoàng Mai. Hà Nội.Số lượng trụ sở68833Sản phẩmQuạt điện, ổ cắm, động cơ, linh kiện,...Thương hiệuCông ty Điện cơ thống nhấtTổng v

Bahasa HokkienDialek Zhangzhou 漳州話 / 漳州话 (Chiang-chiu-ōa) Pengucapan[tsiaŋ˨ tsiu˨ ua˨]Dituturkan diTiongkok daratan, Taiwan, Singapura, Malaysia, Indonesia dan Filipina.Wilayahkota Zhangzhou, provinsi Fujian bagian selatanPenuturSekitar 4 jutaRumpun bahasaSino-Tibet SinitikMinMin PesisirMin SelatanHokkienHokkienDialek Zhangzhou Kode bahasaISO 639-3–Glottologfuji1236Linguasfer79-AAA-jedLokasi penuturan Dialek ZhangzhouPeta bahasa lain Artikel ini mengandung simbol...

1983 single by Joe WalshSpace Age Whiz KidsSingle by Joe Walshfrom the album You Bought It – You Name It Released1983Recorded1982Genre Rock new wave Length3:40Label Warner Bros. Full Moon Songwriter(s) Joe Vitale Joe Walsh Producer(s)Bill SzymczykJoe Walsh singles chronology The Waffle Stomp (1982) Space Age Whiz Kids (1983) I Can Play That Rock & Roll (1983) Space Age Whiz Kids is a song by Joe Walsh, the guitarist for the Eagles. It was released as a lead single from his sixth studio ...

Artikel ini sudah memiliki daftar referensi, bacaan terkait, atau pranala luar, tetapi sumbernya belum jelas karena belum menyertakan kutipan pada kalimat. Mohon tingkatkan kualitas artikel ini dengan memasukkan rujukan yang lebih mendetail bila perlu. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) UDP, singkatan dari User Datagram Protocol, adalah salah satu protokol lapisan transpor TCP/IP yang mendukung komunikasi yang tidak andal (unreliable), tanpa koneksi (connectio...

Head of state of the Republic of Burundi President of theRepublic of BurundiPrésident de la République du BurundiCoat of arms of BurundiIncumbentÉvariste Ndayishimiyesince 18 June 2020Executive branch in Burundian politicsStyleHis ExcellencyStatusHead of stateHead of governmentTerm length7 yearsRenewable onceConstituting instrumentConstitution of BurundiFormation28 November 1966First holderMichel MicomberoDeputyVice-President of BurundiSalary47,300 USD annually[1]WebsiteOffici...

American singer and rapper This article is about the artist. For his self-titled album, see Sean Kingston (album). Sean KingstonSean Kingston in 2013Background informationBirth nameKisean Paul AndersonBorn (1990-02-03) February 3, 1990 (age 33)Miami, Florida, U.S.OriginKingston, JamaicaGenres Dancehall R&B hip hop[1] Occupation(s)SingerrapperYears active2007–presentLabelsEmpireE1Time Is MoneyEpicBeluga HeightsMusical artist Kisean Paul Anderson[2] (born February 3, ...

American politician (born 1963) Serena DiMasoMember of the New Jersey General Assemblyfrom the 13th districtIn officeJanuary 9, 2018 – January 11, 2022Serving with Gerard ScharfenbergerPreceded byDeclan O'ScanlonSucceeded byVicky FlynnMember of the Monmouth County Board of Chosen FreeholdersIn officeJanuary 14, 2012 – January 9, 2018Preceded byRobert D. CliftonSucceeded byGerard Scharfenberger Personal detailsBorn (1963-05-17) May 17, 1963 (age 60)Political ...

Societal privilege based on skin lightness White Privilege redirects here. For other uses, see White Privilege (disambiguation). Part of a series onDiscrimination Forms Institutional Structural Attributes Age Caste Class Dialect Disability Genetic Hair texture Height Language Looks Mental disorder Race / Ethnicity Skin color Scientific racism Rank Sex Sexual orientation Species Size Viewpoint Social Arophobia Acephobia Adultism Anti-albinism Anti-autism Anti-homelessness Anti-drug ad...

Island in Southwest Papua, Indonesia DoomNative name: Pulau Doom/DumDoom in 1955Doom (centre of map) among the islands off SorongDoomLocation in Southwest PapuaShow map of West Papua (province)DoomLocation in Western New GuineaShow map of Western New GuineaGeographyCoordinates0°53′13″S 131°14′10″E / 0.88694°S 131.23611°E / -0.88694; 131.23611Adjacent toSouth Pacific OceanCoastline4.5 km (2.8 mi)AdministrationIndonesiaProvinceSouthwest PapuaCitySor...

2006 American filmZzyzxPromotional posterDirected byRichard HalpernWritten byArt D'AlessandroProduced byRichard HalpernStarringKenny JohnsonRobyn CohenRyan FoxKayo ZepedaMusic byKays Al-AtrakchiProductioncompanyYarble.comRelease date February 4, 2006 (2006-02-04) Running time80 minutesCountryUnited StatesLanguageEnglishBudget$1,000,000 (estimated) Zzyzx is a 2006 thriller film produced and directed by Richard Halpern and starring Kenny Johnson, Robyn Cohen, Ryan Fox, and Kayo Z...

Japanese gods Marker dedicated to one of the Chimata-No-Kami, Douso-jin (道祖神) Kunado-no-Kami (Japanese: 岐の神), alternately Kunato-no-Kami, Funado-no-Kami, Funato-no-Kami, or Chimata-no-Kami, are Japanese local gods connected chiefly with protection against disaster and malicious spirits.[1] The term Kunado-no-Kami and its variants are derived ultimately from Japanese: 来な処 ku-na-do, meaning a place that is not to be entered, a taboo or sacred space.[2] These ka...

Business school of the University of South Wales South Wales Business SchoolTypeBusiness SchoolEstablished2013 (2013)Parent institutionUniversity of South WalesLocationNewport and Treforest, WalesWebsiteOfficial website The South Wales Business School is the Business School of the University of South Wales and was established in 2013. The school is currently situated in the Faculty of Creative Industries.[1] It has expertise up to professorial level in the areas of finance and ac...

過海隧道巴士935線Cross Harbour Tunnel Route 935概覽營運公司九龍巴士所屬車廠荔枝角車廠(L)使用車輛Enviro 500 MMC(ATENU)早上由石籬(大隴街)開出班次從905線抽調車輛行走线路信息线路類型繁忙時間路線起點站石籬(大隴街)/安蔭(部份去程班次)途經石蔭邨、青葵公路、西九龍公路、西區海底隧道、中環、金鐘終點站灣仔(菲林明道)线路长度19公里运行周期63分鐘起點�...

American politician Charence C. HoffmanMember of the Iowa House of Representativesfrom the 55th districtIn office1998–2008Preceded byCharles LarsonSucceeded byJason Schultz Personal detailsBorn (1933-08-07) August 7, 1933 (age 90)Leola, South DakotaPolitical partyRepublicanSpouseLynnResidenceCharter Oak, IowaAlma materSouth Dakota State UniversityWebsiteHoffman's website Clarence C. Hoffman (born August 7, 1933) served in the Iowa House of Representatives 1998–2008, m...

English literary scholar Miriam AllottProf. AllottBorn1920Fulham, London, EnglandDied2010 (aged 89–90)Liverpool, EnglandNationalityBritishOccupationProfessorEmployer(s)Liverpool UniversityBirkbeck College Miriam Allott or Miriam Farris; Miriam Farris Allott; Miriam Allott-Farris (1920–2010) was an English literary scholar. She was a professor in Liverpool and at Birkbeck College. Life Allott was born in Cairo[1] or Fulham in 1920. This was just after her father Labib Farr...

List of events ← 2017 2016 2015 2018 in Iran → 2019 2020 2021 Decades: 1990s 2000s 2010s 2020s See also:Other events of 2018Years in Iran Events in the year 2018 in Iran. Incumbents Supreme Leader of Iran: Ali Khamenei President of Iran: Hassan Rouhani Parliament of Iran: Ali Larijani Judiciary System of Iran: Sadeq Larijani Events January January 1 – As protests continue from last year, ten people are killed in the streets overnight.[1] January 4 – The United States t...