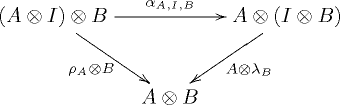
Categoria monoidale
|
Read other articles:

Questa voce o sezione sull'argomento veicoli militari è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più precisamente. Segui i suggerimenti del progetto di riferimento. Fiat 2800DescrizioneTipoveicolo traspo...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (décembre 2019). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références » En pratique : Quelles sources sont attendues ? ...

صيغة ريدبرغ تستخدم في الفيزياء الذرية لوصف الخطوط الطيفية للعديد من العناصر الكيميائية وقد صاغها العالم السويدي يوهانس رايدبيرغ وأعلنها في 5 نوفمبر 1888 .[1][2] مجموعة خطوط لايمان في الفيزياء والكيمياء سلسلة لايمان أو مجموعة خطوط لايمان (Lyman series) سلسلة انبعاث الأشعة فو...

Politics of Mauritania Member State of the Arab League Constitution Human rights Slavery Government President Mohamed Ould Ghazouani Prime Minister Mohamed Ould Bilal Parliament National Assembly President Administrative divisions Regions Departments Communes Elections Recent elections Presidential: 201420192024 Parliamentary: 201320182023 Political parties Electoral districts Foreign relations Ministry of Foreign Affairs Minister: Ismail Ould Cheikh Ahmed Diplomatic missions of / in Mauritan...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) 78° خط طول 78 غرب خريطة لجميع الإحداثيات من جوجل خريطة لجميع الإحداثيات من بينغ تصدير جميع الإحداثيات من كي...

Prof. Dr.Yeheskiel Minggus Tiranda S.H., M.H.\Ketua Tim Manajemen Perubahan untuk Pembaruan Sistem Inti Administrasi PajakMasa jabatan2020 – SekarangKepala Sub Direktorat Kerjasama dan Kemitraan Direktorat Pelayanan, Penyuluhan dan Hubungan Masyarakat Ditjen PajakMasa jabatan2016–2020Kepala Kantor Pelayanan Pajak Pratama Purworejo, Kanwil Ditjen Pajak Jawa Tengah IIMasa jabatan2015–2016Kepala Kantor Pelayanan Pajak Pratama Purbalingga, Kanwil Ditjen Pajak Jawa Tengah IIMasa jab...

Dutch Egyptologist Adriaan de BuckAdriaan de Buck, ca. 1930Born(1892-09-22)22 September 1892Oostkapelle, the NetherlandsDied28 October 1959(1959-10-28) (aged 67)Leiden, the NetherlandsNationalityDutchOccupationEgyptologistYears active1922–1959SpouseAnna Elisabeth NordenbergChildrenAnn-Kjersti, Ingrid and Pieter de BuckAwardsKNAW memberAcademic backgroundAlma materLeiden UniversityThesisDe Egyptische voorstellingen betreffende den oerheuvel (1922)Doctoral advisorWilliam Brede ...

BakmiBakmi disajikan dengan dagingNama lainBakmieJenisMiSajianMenu utamaTempat asal IndonesiaDaerahNasionalDibuat olehTionghoa-JawaSuhu penyajianPanasBahan utamaMi (tepung terigu sebagai bahan baku), daging, jamur, kecapVariasiBakmi kuah, bakmi goreng, mi ayam Media: Bakmi Bakmi (Hokkien: 肉麵; dialek xiamen: bah mi) adalah salah satu jenis sajian mi yang dipopulerkan oleh pedagang-pedagang Tiongkok ke Indonesia. Bakmi juga sering disebut yamien atau yahun. Bakmi juga merupak...

1932 film Dance TeamTheatrical release posterDirected bySidney LanfieldScreenplay byEdwin J. BurkeStarringJames DunnSally EilersRalph MorganMinna GombellEdward CrandallNora LaneCinematographyJames Wong HoweEdited byMargaret ClanceyProductioncompanyFox Film CorporationDistributed byFox Film CorporationRelease date January 17, 1932 (1932-01-17) Running time76 minutesCountryUnited StatesLanguageEnglish Dance Team ad in The Film Daily, 1932 Dance Team is a 1932 American Pre-Code co...

Konfrontasi Indonesia-MalaysiaBagian dari Pembentukan Malaysia dan Perang DinginSeorang tentara Inggris ditarik oleh helikopter Westland Wessex selama operasi di Kalimantan, Agustus 1964Tanggal20 Januari 1963 –11 Agustus 1966(3 tahun, 6 bulan, 3 minggu dan 1 hari)LokasiSemenanjung Malaka, KalimantanHasil Kesepakatan Damai Indonesia menerima pembentukan Malaysia Soekarno digantikan oleh Soeharto menyusul upaya kudeta G30S Pemberontakan Komunis di Sarawak berlanjut hingga ...

1989 crime novel by Peter Robinson A Necessary End First editionAuthorPeter RobinsonCountryCanadaLanguageEnglishSeriesInspector Alan Banks, #3GenreCrime novelPublisherViking PressPublication date1989Media typePrint (Hardback), (Paperback)ISBN0-330-49163-6OCLC49906721Preceded byA Dedicated Man Followed byThe Hanging Valley A Necessary End is the third novel by Canadian detective fiction writer Peter Robinson in the Inspector Banks series. It was published in 1989, and...

Aslan Aliyevich MaskhadovАслан Алиевич МасхадовPresiden Republik Chechnya Ichkeria ke-3Masa jabatan12 February 1997 – 8 Maret 2005PendahuluZelimkhan YandarbiyevPenggantiAbdul-Halim Sadulayev Informasi pribadiLahir21 September 1941Karaganda, RSS Kazakhstan, Uni SovietMeninggal8 Maret 2005(2005-03-08) (umur 63)Tolstoy-Yurt, ChechnyaKebangsaanChechenPartai politikPartai Demokratik VainakhSuami/istriKusama MaskhadovaAnak3ProfesiPerwira (militer)Tanda tanganSunt...

دورة فرنسا المفتوحة 1968 - فردي الرجال جزء من دورة فرنسا المفتوحة 1968 البلد فرنسا التاريخ 1968 الرياضة كرة المضرب البطل(ة) كين روزوول الوصيف(ة) رود ليفر النتيجة 6–3، 6–1، 2–6، 6–2 دورة فرنسا المفتوحة 1969 - فردي الرجال تعديل مصدري - تعديل في دورة فرنسا المفتوحة ...

Chemical compound NS-2359Clinical dataATC codenoneIdentifiers IUPAC name (1R,2R,3S,5S)-3-(3,4-dichlorophenyl)-2-(methoxymethyl)-8-azabicyclo[3.2.1]octane PubChem CID11408320UNII76H76554PAChemical and physical dataFormulaC15H19Cl2NOMolar mass300.22 g·mol−13D model (JSmol)Interactive image SMILES Clc1ccc(cc1Cl)C(C2COC)CC3NC2CC3 (verify) NS-2359 (GSK-372,475) is a serotonin-norepinephrine-dopamine reuptake inhibitor. It was under development by GlaxoSmithKline (GSK) as an ant...

Disused railway line in Wales 53°24′34″N 4°20′55″W / 53.4095°N 4.3486°W / 53.4095; -4.3486 Anglesey Central RailwayOverviewLocaleWalesContinues asLondon and North Western RailwayHistoryOpened16 December 1864TechnicalLine length17+3⁄4 miles (28.6 km)Track gauge4 ft 8+1⁄2 in (1,435 mm) standard gauge vteAnglesey CentralRailway Legend Amlwch Associated Octel Amlwch 17 mi 60 ch28.57 km Rhosgoch ...

この項目では、2004年までのバファローズについて説明しています。2005年以降のバファローズについては「オリックス・バファローズ」をご覧ください。 大阪近鉄バファローズ Osaka Kintetsu Buffaloes会社名 株式会社大阪バファローズ創設 1949年解散 2004年ロゴデザイン 所属リーグ パシフィック・リーグ歴代チーム名 近鉄パールス(1949年 - 1958年) 近鉄バファロー(1959年 - 1...

South Korean web browser Naver Whale네이버 웨일Whale browser on Windows 11, WikipediaDeveloper(s)Naver CorporationInitial releaseMarch 14, 2017; 6 years ago (2017-03-14)Stable release(s)Windows3.22.205.26[1] / 10 October 2023MacOS3.22.205.26[1] / 10 October 2023Android3.0.3.2[2] / 19 October 2023iOS3.0.6[3] / 7 November 2023 EnginesBlinkWebKit (iOS)Operating systemWindows 7 or laterOS X 10.10 or laterUbuntuAndroidi...

Wren Library building The Lincoln Cathedral Library is a library of Lincoln Cathedral in Lincolnshire, England. It is housed in a building designed by Christopher Wren. Collections The collection includes 120 “incunabula”, that is books printed before 1500. As well as a reference collection of c.10,000 items, there are 260 mediaeval manuscripts, including works of theology, canon law, devotional books, music and literature, and the following:[1] Text of the Venerable Bede Lincoln'...

Men's 200 metre freestyle S3at the XV Paralympic GamesVenueOlympic Aquatics StadiumDates15 September 2016Competitors8 from 6 nationsMedalists Wenpan Huang China Dmytro Vynohradets Ukraine Hanhua Li China Swimming at the2016 Summer ParalympicsMen's events50 m freestyleS3S4S5S6S7S8S9S10S11S12S13100 m freestyleS4S5S6S7S8S9S10S11S13200 m freestyleS2S3S4S5S14400 m freestyleS6S7S8S9S10S11S1350 m backstrokeS1S2S3S4S5100 m backstrokeS1S2S6S7S8S9S10S11S12S13S1450 m breasts...

Sèvres komunumo en Francio Blazono Administrado Ĝemelurboj Wolfenbüttel • Mount Prospect vd INSEE kodo 92072 [+] Poŝtkodo 92310 En TTT Oficiala retejo [+] Demografio Loĝantaro 22 618 (2021) [+] Loĝdenso 5 785 loĝ./km² Geografio Geografia situo 48° 49′ N, 2° 13′ O (mapo)48.8230555555562.2108333333333Koordinatoj: 48° 49′ N, 2° 13′ O (mapo) [+] Alto 95 m [+] Areo 3,91 km² ( 39...