Pita Möbius
|
Read other articles:

Potret resmi, 2019 John William Jay Raymond[1] adalah seorang jenderal Angkatan Antariksa Amerika Serikat yang menjabat sebagai kepala operasi antariksa pertamanya. Ia sebelumnya menjabat sebagai panglima Komando Antariksa Amerika Serikat, sebuah jabatan yang ia emban dari 29 Agustus 2019 sampai 20 Agustus 2020. Referensi ^ Clemson Commencement Program. Clemson.edu. May 1984. Diakses tanggal 2019-03-26. Artikel ini berisi bahan berstatus domain umum dari Pemerintah Am...

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada.Este aviso fue puesto el 4 de mayo de 2020. Hey Arnold! The Movie Título ¡Oye, Arnold! La películaFicha técnicaDirección Tuck TuckerProducción Craig BartlettAlbie HechtMarjorie CohnGuion Craig BartlettBasada en ¡Oye, Arnold! de Craig BartlettMúsica Jim LangMontaje Christopher HinkProtagonistas Spencer KleinFrancesca SmithJamil Walker SmithDan CastellanetaTress MacNeille Ver todos los créditos ...

III Copa Mundial de Clubes de la FIFAJapón 2006 FIFAクラブワールドカップ2006(FIFA Kurabu Wārudo Kappu 2006) Sede Japón Japón Espectadores 302.142 (43.163 por partido) Fecha 10 de diciembre de 200617 de diciembre de 2006 Cantidad de equipos 6 de 6 confederaciones Podio • Campeón• Subcampeón• Tercer lugar• Cuarto lugar Internacional Barcelona Al-Ahly América Partidos 7 Goles anotados 17 (2,43 por partido) Goleador Mohamed Aboutrika (3)(Al-Ahly) Bal...

Reina Aba Aba fue a mediados del siglo I d. C. la regente de la ciudad y el reino de Olba en Cilicia. Ella era la hija de Zenófanes que había ejercido en él durante la tiranía de Tracheiotis. Poco a poco fue haciéndose con el poder a través de las relaciones de su padre que en esos momentos era procurador. Agasajó de regalos y presentes a personalidades muy importantes como la faraona de Egipto Cleopatra VII y al triunviro romano Marco Antonio y estos le correspondieron ...

North American collegiate fraternity Delta Kappa EpsilonΔΚΕFoundedJune 22, 1844; 179 years ago (1844-06-22)No. 12 Old South Hall, Yale University, New Haven, ConnecticutTypeSocialAffiliationNICScopeInternationalMottoΚηροθεν Φιλοι ἀει (Kērothen Philoi Aei; Friends From The Heart, Forever)Colors Azure (Blue/Navy) Gold (Or) Gules (Crimson)SymbolRampant LionFlagPublicationThe Deke QuarterlyPhilanthropyRampant Lion FoundationChapters56Colonie...

Pour les articles homonymes, voir Agios Nikolaos. Ágios Nikólaos (el) Άγιος Νικόλαος Ágios Nikólaos et le lac Voulismeni. Administration Pays Grèce Périphérie Crète District régional Lassíthi Dème Dème d'Ágios Nikólaos Code postal 721 00 Indicatif téléphonique 28410 Immatriculation AN Démographie Population 19 593 hab. (2001[1]) Densité 62 hab./km2 Géographie Coordonnées 35° 11′ 21″ nord, 25° 43′ 02″ est A...

Colombian footballer (born 1991) In this Spanish name, the first or paternal surname is Zapata and the second or maternal family name is Banguero. Duván Zapata Zapata playing for Napoli in 2014Personal informationFull name Duván Esteban Zapata BangueroDate of birth (1991-04-01) 1 April 1991 (age 32)[1]Place of birth Padilla, Cauca, ColombiaHeight 1.89 m (6 ft 2 in)[2]Position(s) ForwardTeam informationCurrent team Torino(on loan from Atalanta)Numb...

Автентичне виконавство, Автентизм (від пізньолат. authenticus — справжній, достовірний) — рух в музичному виконавстві, що ставить своїм завданням максимально точне відтворення звучання музики минулого, відповідність сучасного виконання оригінальним, «історичним» уяв�...

Television series The Last MatchGenreDrama SportsStarringSon Ji-chang Lee Sang-ah Jang Dong-gun Shim Eun-ha Lee Jong-won Shin Eun-kyungCountry of originSouth KoreaOriginal languageKoreanNo. of episodes16ProductionProduction locationSouth KoreaRunning time60 minutes Mondays and Tuesdays at 21:50 (KST)Original releaseNetworkMBCReleaseJanuary 3 (1994-01-03) –February 22, 1994 (1994-02-22) The Last Match (Korean: 마지막 승부; RR: Majimak Seungbu) is a 1...

Wiz Khalifa discographyWiz Khalifa performing in 2018Studio albums7Music videos82EPs3Singles84Soundtrack albums1Mixtapes24Promotional singles16Compilation albums1Collaborative albums2 American rapper Wiz Khalifa has released seven studio albums, one compilation album, one soundtrack album, three extended plays (EP), two collaborative albums, 84 singles (including 44 as a featured artist), sixteen promotional singles, twenty-one mixtapes, and 82 music videos. After signing to independent recor...

City in Ohio, United StatesShaker HeightsCityShaker Village Historic DistrictLocation in Cuyahoga County and the state of Ohio.Coordinates: 41°28′35″N 81°33′6″W / 41.47639°N 81.55167°W / 41.47639; -81.55167CountryUnited StatesStateOhioCountyCuyahogaEstablished1911Incorporated1912Government • MayorDavid Weiss (D)Area[1] • Total6.33 sq mi (16.40 km2) • Land6.29 sq mi (16.29 km2) �...

Village and civil parish in the East Lindsey district of Lincolnshire, England Human settlement in EnglandToynton St PeterSt Peter's Church, Toynton St PeterToynton St PeterLocation within LincolnshirePopulation256 (2011)[1]OS grid referenceTF404632• London115 mi (185 km) SDistrictEast LindseyShire countyLincolnshireRegionEast MidlandsCountryEnglandSovereign stateUnited KingdomPost townSPILSBYPostcode districtPE23PoliceLincolnshireFi...

Genus of lizards Laudakia stellio Dana Biosphere Reserve, Jordan Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Reptilia Order: Squamata Suborder: Iguania Family: Agamidae Genus: Laudakia Species: L. stellio Binomial name Laudakia stellio(Linnaeus, 1758) Synonyms[2] Lacerta stellio Linnaeus, 1758 Agama stellio — Boulenger, 1885 Stellio stellio — Kasparek, 1990 Placoderma stelli...

Эту статью предлагается удалить.Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/13 июня 2022.Пока процесс обсуждения не завершён, статью можно попытаться улучшить, однако следует воздерживаться от переименований или немотив...

تحتاج هذه المقالة إلى الاستشهاد بمصادر إضافية لتحسين وثوقيتها. فضلاً ساهم في تطوير هذه المقالة بإضافة استشهادات من مصادر موثوقة. من الممكن التشكيك بالمعلومات غير المنسوبة إلى مصدر وإزالتها. (نوفمبر 2018) حرب الجزائر جزء من الحرب الباردة أسبوع الحواجز في الجزائر العاصم...

Range of neurodevelopmental conditions For general learning disability, see Intellectual disability. Slow learner redirects here. For other uses, see Slow learner (disambiguation). Medical conditionLearning disabilityOther namesLearning difficulties,[1][2] developmental academic disorder,[3][4] nonverbal learning disorder,[4] developmental disorder of scholastic skills, unspecified,[4] knowledge acquisition disability NOS,[4] learning di...

Distorsi kognitif adalah berpikiran secara berlebihan dan tidak rasional yang menyebabkan gangguan psikologis tertentu. Kognitif berasal dari bahasa Latin abad pertengahan cognitīvus, atau cognit yang artinya dikenal. Distorsi bermakna tindakan memutar atau mengubah sesuatu dari keadaan sebenarnya atau aslinya.[1] Teori distorsi kognitif pertama kali diajukan oleh David D. Burns, MD.[2] Individu yang mengalami distorsi kognitif menyebabkan pikirannya merasakan realitas secara...
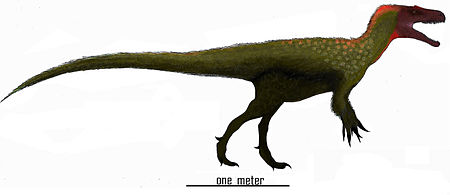
MarshosaurusRentang fosil: Jura Akhir, 155–152 jtyl PreЄ Є O S D C P T J K Pg N ↓ Tengkorak Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata (tanpa takson): Klad DinosauriaKlad SaurischiaKlad Theropoda Famili: †Piatnitzkysauridae Genus: †MarshosaurusMadsen, 1976[1] Spesies: †M. bicentisimus Nama binomial †Marshosaurus bicentisimusMadsen, 1976[1] Marshosaurus adalah genus dinosaurus theropoda karnivora berukuran sedang dari famili Megalosauroid...

Cet article est une ébauche concernant une étoile. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Consultez la liste des tâches à accomplir en page de discussion. PZ Cassiopeiae PZ Cassiopeiae est l'étoile brillante située en haut et à droite de cette image infrarouge de WISE. Données d'observation(époque J2000.0) Ascension droite 23h 44m 03,28104s[1] Déclinaison +61° 47′ 22...

Bendera Åland Templat:Skandinavia Sejarah Åland dapat ditelusuri dari 4000 SM, ketika manusia mencapai kepulauan tersebut untuk pertama kalinya pada periode Neolitikum.[1] Beberapa desa dari Zaman Perunggu dapat ditemukan di Åland. Pada Zaman Viking, dibangun enam benteng bukit. Swedia menguasai Kepulauan Åland dari 1200an hingga 1809, selama periode tersebut, Kastel Kastelholm merupakan lokasi bagi banyak pertempuran. Pada 1809, Kekaisaran Rusia mengambil alih Åland dan Finlandi...










