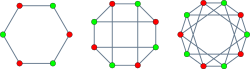
Koronagráf (gráfelmélet)
| |||||||||||||||||||||||||
Read other articles:

The Park Inn pada 2006, setelah selesainya façade barunya Hotel saat direnovasi, dengan façade 1970 aslinya Park Inn Berlin-Alexanderplatz merupakan bangunan bertingkat tertinggi di Berlin. Hotel bertingkat 41 ini terletak di Alexanderplatz dan memiliki tinggi 132 meter. Dibangun dengan nama Hotel Stadt Berlin', bagian dari organisasi Interhotel Jerman Timur, dari 1967 hingga 1970. Pada tingkat paling atas, terdapat sebuah kasino dan restoran. Pada 1993, setelah penyatuan kembali Jerman, na...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مايو 2023) أرمورد كور فورمولا فرونت المطور فروم سوفتوير الناشر JP FromSoftwareNA إيج تيكAU Red Ant EnterprisesEU 505 غيمز المخرج Nozomu Iwai المبرمج Nobuhiko Yoshino المنتج Toshifumi Nabeshima الموسيقى Tsukasa SaitohAy...

У Вікіпедії є статті про інших людей із прізвищем Краснов. Краснов Іван КузьмичНародився 1752Буканівська, Хоперський округ, Російська імперіяПомер 25 серпня (6 вересня) 1812Бородіно (Московська область), Можайський повітd, Московська губернія, Російська імперіяПоховання Стари

Canal JDiluncurkan23 Desember 1985PemilikM6 GroupNegara PrancisSitus webwww.canalj.net Canal J merupakan sebuah jaringan televisi Prancis yang ditujukan kepada program anak-anak. Tersedia melalui layanan televisi terrestrial digital 'TNT' dan ditujukan pada anak berusia antara 4 dan 16 tahun. Program Code Lyoko Dragon Booster Kid Paddle My Life Me Totally Spies Marsupilami Martin Mystery (animated series) Oggy And The Cockroaches Sabrina, the Animated Series Skyland Trollz Viva Pinata Yu...

شتاينهايم شعار الاسم الرسمي (بالألمانية: Steinheim an der Murr) الإحداثيات 48°58′00″N 9°17′00″E / 48.966666666667°N 9.2833333333333°E / 48.966666666667; 9.2833333333333 [1] تقسيم إداري البلد ألمانيا[2] خصائص جغرافية المساحة 23.18 كيلومتر مربع (2006)[3][4] ارتفاع 200 �...

1952 film For 1973 film, see Daag: A Poem of Love. DaagTheatrical posterDirected byAmiya ChakravartyWritten byRajinder Singh BediScreenplay byAmiya Chakravarty Rajendra ShankarStory byAmiya Chakravarty Rajendra ShankarProduced byAmiya ChakravartyStarringDilip KumarNimmiCinematographyV. BabasahebEdited byD. B. JoshiMusic byShankar–JaikishanProductioncompanyMars & Movies ProductionsDistributed byMars & Movies ProductionsRelease date4 July 1952 (1952-07-04)Running time14...

This article is part of a series onTaxation in the United States Federal taxation Alternative minimum tax Capital gains tax Corporate tax Estate tax Excise tax Gift tax Generation-skipping transfer tax Income tax Payroll tax Internal Revenue Service (IRS) Internal Revenue Code (IRC) IRS tax forms Revenue by state History Constitutional authority Taxpayer standing Court Protest Evasion Resistance State and local taxation State income tax Property tax Sales tax State and local tax deduction Use...

Kharilaos (Harilaos), juga disebut Kharillos (Yunani: Χαρίλαος), merupakan seorang raja Sparta pada awal pertengahan abad ke-8 SM. Menurut Pausanias, Kharilaos adalah penerus ayahandanya Polydectes.[1] Kharilaos adalah keponakan reformator Sparta, Lykourgos.[2] Selama masa pemerintahannya, Sparta menyerang Argolis. Permusuhan lama dengan Tegeia juga diyakini berasal dari masa pemerintahan Kharilaos.[1] Kharilaos digantikan oleh putranya Nikandros, ayahanda Theo...

Species of beetle Rhembastus variabilis Rhembastus variabilis Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Coleoptera Infraorder: Cucujiformia Family: Chrysomelidae Genus: Rhembastus Species: R. variabilis Binomial name Rhembastus variabilisHarold, 1877[1] Synonyms Rhambastus variabilis var. madoni Pic, 1952[2] Rhambastus variabilis var. paulojunctus Pic, 1952[2] Rhambastus variabilis var. separatus Pic, 19...

City municipality in Vojvodina, SerbiaCity municipality of Novi Sad Градска општина Нови СадGradska opština Novi SadCity municipalityCity municipality of Novi SadLocation within Novi SadShow map of Novi SadCity municipality of Novi SadCity municipality of Novi Sad (Vojvodina)Show map of VojvodinaCity municipality of Novi SadCity municipality of Novi Sad (Serbia)Show map of SerbiaCity municipality of Novi SadCity municipality of Novi Sad (Europe)Show map of EuropeCoordina...

Sudut kota Évreux Évreux merupakan salah satu kota di Prancis. Letaknya di bagian utara. Tepatnya di region Haute-Normandie. Pada tahun 1999, kota ini memiliki jumlah penduduk sebanyak 51.198 jiwa dengan memiliki luas wilayah 26,45 km². Kota ini memiliki angka kepadatan penduduk sebesar 1.936 jiwa/km². Pranala luar Wikimedia Commons memiliki media mengenai Évreux. Situs resmi lbsKomune di departemen Eure Aclou Acon Acquigny Aigleville Ailly Aizier Ajou Alizay Ambenay Amécourt Amfre...

Syrian politician You can help expand this article with text translated from the corresponding article in Arabic. Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Consider adding a topic to this template: there are al...

American historian J. A. C. ChandlerChandler pictured in The Colonial Echo 1920, William and Mary yearbook18th President of theCollege of William & MaryIn office1919–1934Preceded byLyon Gardiner TylerSucceeded byJohn Stewart Bryan Personal detailsBorn(1872-10-29)October 29, 1872Caroline County, VirginiaDiedMay 31, 1934(1934-05-31) (aged 61)Norfolk, VirginiaAlma materCollege of William & Mary Johns Hopkins University Julian Alvin Carroll Chandler (October 29, 1872 – May 31...

1934 book The Scandal of Sophie Dawes First US editionAuthorMarjorie BowenCountryUnited KingdomLanguageEnglishGenreHistorical non fictionPublisherJohn Lane (London) Appleton (New York)Publication date1934Media typePrint The Scandal of Sophie Dawes is a 1934 historical non-fiction work by Marjorie Bowen.[1] It is based on the life of the Sophie Dawes, Baronne de Feuchères an English adventuress who became a courtesan in Restoration France following the fall of Napoleon.[2]...

Sant'Ivo di ChartresMiniatura raffigurante sant'Ivo Vescovo Nascita1040, Beauvais Morte23 dicembre 1115 Venerato daChiesa cattolica Ricorrenza23 dicembre Manuale Ivo o Ivone di Chartres (Beauvais, 1040 – 23 dicembre 1115) fu canonista e vescovo di Chartres; è venerato come santo dalla Chiesa cattolica. Indice 1 Biografia 2 La lotta per le investiture 3 Opere 3.1 Manoscritti 4 Genealogia episcopale e successione apostolica 5 Note 6 Altri progetti 7 Collegamenti esterni Biografia ...

Monarch butterfly This list contains links to lists with the common and scientific names of butterflies of North America north of Mexico. Papilionidae: swallowtails and parnassians (40 species) Parnassiinae: parnassians (3 species) Papilioninae: swallowtails (37 species) Hesperiidae: skippers (300 species) Pyrrhopyginae: firetips (1 species) Pyrginae: spread-wing skippers (138 species) Heteropterinae: skipperlings (7 species) Hesperiinae: grass skippers (141 species) Megathyminae: giant-skipp...

Captain Kirk Douglas Información personalNacimiento 30 de septiembre de 1972 (51 años)Nacionalidad EstadounidenseInformación profesionalOcupación Músico y guitarrista Años activo desde 1993Géneros Hip hop, neo soul, soul, funk, rhythm and blues, pop alternativo y pop Instrumentos Guitarra, ukelele y voz [editar datos en Wikidata] Captain Kirk Douglas es un guitarrista y cantante estadounidense que actúa con la banda de hip hop The Roots. Se unió a The Roots en 2003. Su prim...

Chaenactideae Chaenactis fremontiiTaxonomíaReino: PlantaeSubreino: TracheobiontaDivisión: MagnoliophytaClase: MagnoliopsidaSubclase: AsteridaeOrden: AsteralesFamilia: AsteraceaeSubfamilia: AsteroideaeTribu: ChaenactideaeB.G.Baldwin, 2002Géneros Ver texto. [editar datos en Wikidata] Chaenactideae es una tribu de plantas con flores perteneciente a la subfamilia Asteroideae dentro de la familia Asteraceae. Tiene los siguientes géneros.[1] La tribu Chaenactideae se cre...

レイクウッド 市 Lakewood レイクウッド・シティホール(2005年) 標語: Tomorrow's City Today ロサンゼルス郡内の位置 北緯33度50分51秒 西経118度7分12秒 / 北緯33.84750度 西経118.12000度 / 33.84750; -118.12000座標: 北緯33度50分51秒 西経118度7分12秒 / 北緯33.84750度 西経118.12000度 / 33.84750; -118.12000国 アメリカ合衆国州 カリフォルニア州郡 ロサンゼルス...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (ديسمبر 2018) مقاطعة كير الإحداثيات 30°04′N 99°21′W / 30.06°N 99.35°W / 30.06; -99.35 ...