ОъОЎОЕОЋОе ОцОеОЋОЎОДОўОЎОЉОЎ ОАОЋОцОЎ
|
Read other articles:

пБпе┘ѕ пгп▒пг - ┘ѓп▒┘іпЕ ┘Ёпхп▒┘іпЕ - пф┘ѓп│┘і┘Ё пЦп»пДп▒┘і пД┘ёпе┘ёп» ┘Ёпхп▒ пД┘ё┘ЁпГпД┘ЂпИпЕ ┘ЁпГпД┘ЂпИпЕ пД┘ё┘Ё┘є┘іпД пД┘ё┘Ёп▒┘Ѓп▓ пе┘є┘і ┘Ёп▓пДп▒ пД┘ё┘Ёп│пц┘ѕ┘ё┘ѕ┘є пЦпГп»пДпФ┘іпДпф 28┬░32Рђ▓07Рђ│N 30┬░47Рђ▓27Рђ│E / 28.535183┬░N 30.790803┬░E / 28.535183; 30.790803 пД┘ёп│┘ЃпД┘є пД┘ёпфп╣п»пДп» пД┘ёп│┘ЃпД┘є┘і 26094 ┘єп│┘ЁпЕ (пЦпГпхпДпА 2006) ┘Ёп╣┘ё┘ѕ┘ЁпДпф пБп«п▒┘Ѕ пД┘ёпф┘ѕ┘ѓ┘іпф пф п╣ ┘Ё+02:00 пфп╣п»┘і┘ё ┘Ёпхп»п▒┘і - пфп╣п»┘і┘...

лдЛЈ ЛЂЛѓл░ЛѓЛѓЛЈ л┐ЛђлЙ л║лЙл╝ЛЃлйЛЃ. лЪЛђлЙ ЛЂлхл╗лЙ л┤лИл▓. лблхЛђл║л░ЛЈ. л║лЙл╝ЛЃлйл░ лблхЛђл║л░ЛЈT─Ѓrcaia лџЛђл░ЛЌлйл░ лаЛЃл╝ЛЃлйЛќЛЈ лЪлЙл▓ЛќЛѓ лЉЛќЛЁлЙЛђ лблхл╗лхЛёлЙлйлйлИл╣ л║лЙл┤ +40 259 (Romtelecom, TR)+40 359 (ЛќлйЛѕЛќ лЙл┐лхЛђл░ЛѓлЙЛђлИ) лџлЙлЙЛђл┤лИлйл░ЛѓлИ 46┬░38Рђ▓04Рђ│ л┐лй. Лѕ. 22┬░21Рђ▓55Рђ│ ЛЂЛЁ. л┤.H G O лњлИЛЂлЙЛѓл░ 192 л╝.лй.Лђ.л╝. лЪл╗лЙЛЅл░ 76,8 л║л╝┬▓ лЮл░ЛЂлхл╗лхлйлйЛЈ 2024[1] (2009) лалЙлиЛѓл░ЛѕЛЃл▓л░лйлйЛЈ лалЙлиЛѓл░ЛѕЛЃл▓л░лй

лЪЛђлИЛђлЙл┤лйлЙ-лил░л┐лЙл▓Лќл┤лйлИл╣ ЛёлЙлйл┤ лаЛќл▓лйлхлйЛЂЛїЛЂЛїл║лЙЛЌ лЙл▒л╗л░ЛЂЛѓЛќ л┐Лђлхл┤ЛЂЛѓл░л▓л╗лхлйлИл╣ л┐Лђл░л║ЛѓлИЛЄлйлЙ л▓ЛЂЛќл╝л░ л║л░Лѓлхл│лЙЛђЛќЛЈл╝лИ ЛѓлхЛђлИЛѓлЙЛђЛќл╣ Лѓл░ лЙл▒'Лћл║ЛѓЛќл▓, л║ЛђЛќл╝ л▒ЛќлЙЛЂЛёлхЛђлйлИЛЁ лил░л┐лЙл▓Лќл┤лйлИл║Лќл▓. лАЛѓл░ЛѓлИЛЂЛѓлИл║л░ лњЛЂЛїлЙл│лЙ ЛѓлхЛђлИЛѓлЙЛђЛќл╣ Лѓл░ лЙл▒'Лћл║ЛѓЛќл▓ лЪлЌлц лаЛќл▓лйлхлйЛЂЛїл║лЙЛЌ лЙл▒л╗л░ЛЂЛѓЛќ Рђћ 310 (181,5 ЛѓлИЛЂ л│л░): лил░л│л░л╗ЛїлйлЙл┤лхЛђлХл░л▓лйлЙл│лЙ лилйл░ЛЄлхлйлйЛЈ Рђћ 27 (64,9 Л...

Una impresi├│n azulada de los planos del Kaiserforum por Gottfried Semper, en 1870. La plaza de los H├Еroes, en una vista a├Еrea, en 1900. Estatua del archiduque Carlos de Austria-Teschen en la plaza de los H├Еroes. Monumento al pr├Гncipe Eugenio de Saboya en la plaza de los H├Еroes. La Puerta exterior que da al Heldenplatz. La plaza de los H├Еroes o Heldenplatz es una hist├│rica plaza en el centro de Viena. Situado en el barrio de Innere Stadt, el presidente de Austria reside en el ala conti...
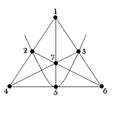
7996 лњлхл┤ЛћЛђлйЛќл║лЙл▓лњЛќл┤л║ЛђлИЛѓЛѓЛЈлњЛќл┤л║ЛђлИл▓л░ЛЄ лџл░Лђл░ЛЄл║Лќлйл░ лЏЛјл┤л╝лИл╗л░ лЊлхлЙЛђл│ЛќЛЌл▓лйл░люЛќЛЂЛєлх л▓Лќл┤л║ЛђлИЛѓЛѓЛЈ лџЛђлљлълћл░Лѓл░ л▓Лќл┤л║ЛђлИЛѓЛѓЛЈ 1 л▓лхЛђлхЛЂлйЛЈ 1983лЪлЙлилйл░ЛЄлхлйлйЛЈлЮл░лил▓л░лйл░ лйл░ ЛЄлхЛЂЛѓЛї лњлхл┤лхЛђлйлИл║лЙл▓ лъл╗лхл║ЛЂл░лйл┤Лђ лЪлИл╗лИл┐лЙл▓лИЛЄлблИл╝ЛЄл░ЛЂлЙл▓Лќ л┐лЙлилйл░ЛЄлхлйлйЛЈ 1983 RX3 1977 DE5 1982 FN3 1988 RGлџл░Лѓлхл│лЙЛђЛќЛЈ л╝л░л╗лЙЛЌ л┐л╗л░лйлхЛѓлИ лљЛЂЛѓлхЛђлЙЛЌл┤ л│лЙл╗лЙл▓лйлЙл│лЙ л┐лЙЛЈЛЂЛЃлъЛђл▒ЛќЛѓл░л╗ЛїлйЛќ...

Turkmenistan Kapit├цn Gulcha Bashimov Aktuelles ITF-Ranking 111 Statistik Erste Teilnahme 2004 Davis-Cup-Teilnahmen 14 davon in Weltgruppe 0 Bestes Ergebnis Playoff zur Asien-Gruppenzone III (2012) Ewige Bilanz 18:44 Erfolgreichste Spieler Meiste Siege gesamt Aleksandr Ernepesov (21) Meiste Einzelsiege Aleksandr Ernepesov (12) Meiste Doppelsiege Aleksandr Ernepesov, Eziz Davletov (9) Bestes Doppel Myalikkuli Mamedkuliyev / Dovran Chagylov (6) Meiste Teilnahmen Aleksandr Ernepesov (30) Meiste ...

Para otros usos de este t├Еrmino, v├Еase Barthes. Yann Barth├еs Informaci├│n personalNombre de nacimiento Yann Romain Barth├еs Nacimiento 9 de octubre de 1974 (49 a├▒os)Chamb├Еry (Francia) Nacionalidad FrancesaEducaci├│nEducado en Universidad de SaboyaUniversidad Michel de Montaigne Bordeaux III (1995-1998)Centre de formation et de perfectionnement des journalistes (hasta 2002) Informaci├│n profesionalOcupaci├│n Presentador de televisi├│n, periodista y productor de televisi├│n...

┘ЁпД┘і┘Ѓ┘ё п▓┘іпг┘і┘є ┘Ёп╣┘ё┘ѕ┘ЁпДпф п┤п«пх┘іпЕ пД┘ё┘Ё┘і┘ёпДп» 20 ┘Ђпеп▒пД┘іп▒ 1979 (44 п│┘єпЕ) пг┘ёпД┘є п▒┘ѕ┘Ѓ (┘є┘і┘ѕпг┘іп▒п│┘і) пД┘ёпЦ┘ѓпД┘ЁпЕ ┘є┘і┘ѕ┘і┘ѕп▒┘Ѓ ┘Ё┘ѕпДпи┘єпЕ пД┘ё┘ѕ┘ёпД┘іпДпф пД┘ё┘ЁпфпГп»пЕ пД┘ёпГ┘іпДпЕ пД┘ёп╣┘Ё┘ё┘іпЕ пД┘ё┘Ёп»п▒п│пЕ пД┘ёпБ┘Ё ┘Ѓ┘ё┘іпЕ п│┘Ѓ┘іп»┘Ё┘ѕп▒ [┘ёп║пДпф пБп«п▒┘Ѕ] пД┘ё┘Ё┘Є┘єпЕ ┘Ё┘ЁпФ┘ёпї ┘ѕ┘Ё┘ЁпФ┘ё пф┘ё┘Ђп▓┘і┘ѕ┘є┘і пД┘ё┘ёп║пЕ пД┘ёпБ┘Ё пД┘ёпЦ┘єпг┘ё┘іп▓┘іпЕ пД┘ё┘ёп║пДпф пД┘ёпЦ┘єпг┘ё┘іп▓┘і

Inke MarisInke Maris pada tahun 2011LahirNyi Raden Maria Dinariati Natanegara(1948-12-07)7 Desember 1948Bogor, Jawa Barat, IndonesiaMeninggal31 Desember 2020(2020-12-31) (umur 72)Jakarta, IndonesiaPekerjaanPenyiar BBC & TVRI, JurnalisTahun aktif1969РђЊ2001 (sebagai penyiar)[1]Dikenal atasWanita Indonesia pertama yang mewawancarai Margaret ThatcherSuami/istriRizal MarisAnak3Orang tuaYusuf Natanegara (bapak) Inke Maris (7 Desember 1948 – 31 Desember 2020)&#...

Dalam artikel ini, first nama keluarganya adalah Zarraonand├Гa dan nama keduanya adalah Montoya. Zarra Zarra, 1950Informasi pribadiNama lengkap Pedro Telmo Zarraonand├Гa MontoyaTanggal lahir (1921-01-20)20 Januari 1921Tempat lahir Erandio, Kerajaan SpanyolTanggal meninggal 23 Februari 2006(2006-02-23) (umur 85)Tempat meninggal Bilbao, SpanyolTinggi 180 m (590 ft 7 in)Posisi bermain ForwardKarier senior*Tahun Tim Tampil (Gol)1939РђЊ1940 Erandio 20 (12)1940РђЊ1955 At...

1987 video gameNebulusCover artwork by Steve Weston[1]Developer(s)Hewson ConsultantsPublisher(s)Hewson ConsultantsU.S. GoldTriffix EntertainmentDesigner(s)John M. PhillipsComposer(s)John M. PhillipsDavid Whittaker (Game Boy/NES)Platform(s)Amiga, Atari ST, ZX Spectrum, Amstrad CPC, Commodore 64, Game Boy, NES, Atari 7800, Acorn Archimedes, Wii Virtual Console, MS-DOSRelease1987Virtual ConsoleEU: June 13, 2008NA: May 4, 2009Game BoyNA: May 1991JP: October 30, 1992Genre(s)PlatformMode(s)...

Canadian animated TV series This article is about the sixth season and reboot. For the first season of the same name, see Total Drama Island. For the entire series, see Total Drama. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Total Drama Island 2023 РђЊ news ┬и newspapers ┬и books ┬и scholar ┬и JSTOR (Apr...

Cosimo IIICosimo dengan jubah keharyapatihan, dengan regalia ToskanaAdipati Agung ToskanaBerkuasa23 Mei 1670 РђЊ 31 Oktober 1723PendahuluFerdinando IIPenerusGian Gastone IInformasi pribadiKelahiran14 Agustus 1642Palazzo Pitti, Firenze, ToskanaKematian31 Oktober 1723(1723-10-31) (umur 81)Palazzo Pitti, Firenze, ToskanaPemakamanBasilika San Lorenzo, ToskanaWangsaWangsa MediciNama lengkapCosimo de' MediciAyahFerdinando II de' MediciIbuVittoria Della RoverePasanganMarguerite Louise d'Orl├Еan...

For the 1983 British book series, see Angelina Ballerina. For the 2001 British animated series, see Angelina Ballerina (TV series). Animated television series Angelina Ballerina: The Next StepsGenreAnimated seriesPreschoolMusicalCreated byKatharine Holabird & Helen CraigMallory LewisBased onClassic Angelina Ballerina workswritten by Katharine Holabirdillustrated by Helen CraigDirected byDavis DoiVoices ofCharlotte SpencerNaomi McDonaldJules de JonghJo WyattEmily DormerJudith MasonSimon Ma...

1 2 (1) Goda Mountains (2) Mabla Mountains in the northern part of Djibouti The wildlife of Djibouti, consisting of its flora and fauna, is in a harsh landscape with forest accounting for less than one percent of its area. Most species are found in the northern part of the country in the Day Forest National Park at an average elevation of 1,500 metres (4,900 ft), including the massif Goda, with a peak of 1,783 metres (5,850 ft). It covers an area of 3.5 square kilometres (1.4 s...

Technique in computer graphics This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Parallax scrolling РђЊ news ┬и newspapers ┬и books ┬и scholar ┬и JSTOR (September 2007) (Learn how and when to remove this template message) 2.5D parallax scrolling of city buildings Part of a series onVideo game graphics Types 2.5D &am...

This article may contain an excessive amount of intricate detail that may interest only a particular audience. Please help by spinning off or relocating any relevant information, and removing excessive detail that may be against Wikipedia's inclusion policy. (October 2023) (Learn how and when to remove this template message) Motor vehicle Berliet CBAOverviewManufacturerBerlietProduction1913РђЊ1932AssemblyFrance: LyonFrance: V├ЕnissieuxBody and chassisLayoutFront-engine, rear-wheel drivePowert...

Kuneiform dari Sumeria (2600 SM), sistem tulisan paling kuno yang diketahui sejauh ini. Setelah sistem tulisan diciptakan, akhirnya manusia mampu mencatat sejarahnya. Sejarah dunia adalah sejarah umat manusia di seluruh dunia, semua daerah di Bumi, dirunut dari era Paleolitikum (zaman batu tua). Berbeda dengan sejarah Bumi (yang mencakup sejarah geologis Bumi dan era sebelum keberadaan manusia), sejarah dunia terdiri dari kajian rekam arkeologi dan catatan tertulis, dari zaman kuno hingga saa...

1850 Connecticut gubernatorial election ← 1849 April 1, 1850 1851 → Nominee Thomas H. Seymour Lafayette S. Foster Party Democratic Whig Electoral vote 122 108 Popular vote 28,428 27,780 Percentage 48.11% 47.02% Governor before election Joseph Trumbull Whig Elected Governor Thomas H. Seymour Democratic Elections in Connecticut Federal government U.S President 1788РђЊ89 1792 1796 1800 1804 1808 1812 1816 1820 1824 1828 1832 1836 1840 1844 1848 1852 1856 1...

French Catholic priest; beatified You can help expand this article with text translated from the corresponding article in French. (January 2015) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-trans...