משפט העקום של ז'ורדן
|
Read other articles:

Secita CeritaAlbum studio karya Achmad AlbarDirilis1981Direkam?GenrepopDurasi?LabelSky RecordsMusica Studio's (rilisan ulang 2021)Kronologi Achmad Albar ?String Module Error: Match not foundString Module Error: Match not found Secita Cerita 1981 Langkahkan Pasti 1982String Module Error: Match not foundString Module Error: Match not found Secita Cerita adalah album dari penyanyi Achmad Albar yang dirilis dengan label Sky Records. Album ini merupakan kerjasama Albar dengan Fariz RM. Daftar ...

Beach in Hong Kong Island, Hong Kong Turtle Cove BeachBeachTurtle Cove BeachTurtle Cove BeachCoordinates: 22°13′59″N 114°13′23″E / 22.23303°N 114.22319°E / 22.23303; 114.22319LocationTai Tam, Hong Kong IslandDimensions • Length73 metresPatrolled byLeisure and Cultural Services Department Turtle Cove BeachTraditional Chinese龜背灣泳灘Simplified Chinese龟背湾泳滩TranscriptionsStandard MandarinHanyu PinyinGuī Bèi Wān Yǒng TānYue...
هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (فبراير 2016) الطريق

العلاقات السنغالية الإسبانية السنغال إسبانيا السنغال إسبانيا تعديل مصدري - تعديل العلاقات السنغالية الإسبانية هي العلاقات الثنائية التي تجمع بين السنغال وإسبانيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه ال�...

Arístides Aristide BriandOrigen GriegoGénero MasculinoSantoral 31 de agostoSignificado hijo del mejorZona de uso común Todo el mundoArtículos en Wikipedia Todas las páginas que comienzan por «Arístides».[editar datos en Wikidata] Arístides es un nombre propio masculino de origen griego en su variante en español. Proviene del griego antiguo Ἀριστείδης (Aristeídēs), y su significado es hijo del mejor. Arístides fue un estadista ateniense del siglo V a...

Kelumapusaura machi Kelumapusaura machi is een plantenetende ornithischische dinosauriër, behorende tot de Euornithopoda, die tijdens het late Krijt leefde in het gebied van het huidige Argentinië. Vondst en naamgeving In de provincie Río Negro werden door een team van het Laboratorio de Anatomía Comparada y Evolución de los Vertebrados (LACEV), met name Julia D’Angelo, Ana P. Moreno, Marcelo P. Isasi, Gonzalo L. Muñoz, Gabriel Lio en Adriel R. Gentil, skeletten gevonden van euornitho...

Це підсторінка документації шаблону Поточна подія.Вона містить інформацію про використання, категорії та інший вміст, що не є частиною оригінальної сторінки шаблону. Цей шаблон не повинен бути підставленим. Використовується Lua: Module:Unsubst Скорочення {{Current}}{ ...

Guy Sebastian Información personalNombre de nacimiento Guy Theodore SebastianNacimiento 26 de octubre de 1981 (42 años) Klang, MalasiaNacionalidad Australiana y malasiaFamiliaCónyuge Jules Sebastian (m. 2008)EducaciónEducado en King's Baptist Grammar School Información profesionalOcupación Cantante, compositor, productor musical, jurado de The X Factor (Australia)Años activo 2003 - presenteGénero SoulR&B contemporáneoPopGospelInstrumento VozGuitarraPianoTecladoBateríaTipo d...

Placodermi Periode 430–360 jtyl PreЄ Є O S D C P T J K Pg N Llandovery akhir – Devon akhi Placodermi Fossil of Bothriolepis panderi showing its caliper-like pectoral finsTaksonomiSuperkerajaanEukaryotaKerajaanAnimaliaFilumChordataKelasPlacodermi McCoy, 1848 OrdoAntiarchi † Arthrodira † Brindabellaspida † Petalichthyida † Phyllolepida † Ptyctodontida † Rhenanida † Acanthothoraci † ?Pseudopetalichthyida † ?Stensioellida †lbs Placodermi (Dari bahasa yunani πλάξ...

Cet article est une ébauche concernant Los Angeles. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Sceau de la ville de Los Angeles. Le sceau de Los Angeles, en Californie. Le bouclier est encerclé par le nom légal de la ville (Ville de Los Angeles) et sa date de fondation (1781). Il a été adopté le 27 mars 1905, par l'ordonnance 10,834 Symboles Autour du cercle marron, il y a des raisins, des olives et de...

The Cambridge History of the Byzantine Empire The Cambridge History of the Byzantine Empire c.500-1492 is a history of the Byzantine Empire published by Cambridge University Press in 2009. It was edited by Jonathan Shepard of the University of Cambridge.[1] The history is made up of 24 chapters in chronological order comprising new and reprinted material, 15 of them having previously appeared in other Cambridge books such as The Cambridge Ancient History and The New Cambridge Medieval...

Snow BowlLambeau Field, the site of the game. Tampa Bay Buccaneers (2–10) Green Bay Packers (5–7) 0 21 Head coach:Leeman Bennett Head coach:Forrest Gregg 1234 Total TB 0000 0 GB 0777 21 DateDecember 1, 1985StadiumLambeau Field, Green Bay, WisconsinRefereeBen DreithAttendance19,856TV in the United StatesNetworkCBSAnnouncersJim Hill and John Dockery The Snow Bowl is the nickname of a National Football League game played on December 1, 1985, between the Green Bay Packers and Tampa Bay Buccan...

吉野家 本企画の賛同企業。ガスト、ケンタッキー・フライド・チキン、モスバーガー、松屋。 『外食戦隊ニクレンジャー』(がいしょくせんたいニクレンジャー)は、2018年(平成30年)に企画された日本の広告企画の一つ、およびその企画で考案された架空の団体。牛丼チェーンの吉野家が、外食産業を盛り上げるために、肉料理を主力商品とする関連企業5社を集っ�...

1940 American animated film produced by Walt Disney FantasiaTheatrical release posterDirected by Samuel Armstrong James Algar Bill Roberts Paul Satterfield Ben Sharpsteen David D. Hand Hamilton Luske Jim Handley Ford Beebe T. Hee Norman Ferguson Wilfred Jackson Story by Joe Grant Dick Huemer Produced by Walt Disney Ben Sharpsteen Starring Leopold Stokowski Deems Taylor Narrated byDeems TaylorCinematographyJames Wong HoweMusic bySee programProductioncompanyWalt Disney ProductionsDistributed by...

This article is about Norton Field in Columbus Ohio. For Norton Air Force Base near San Bernardino, California, see Norton Air Force Base. Airport in Columbus, OhioNorton FieldNorton Field Historical MarkerIATA: noneICAO: noneSummaryLocationColumbus, OhioCoordinates39°58′N 82°53′W / 39.97°N 82.88°W / 39.97; -82.88 Norton Field was an aviation landing field, located in Columbus, Ohio, that operated from 1923 until the early 1950s. It was the first airport establ...

Upazila in Chittagong, BangladeshFulgazi ফুলগাজীUpazilaFields in Dakshin Sreepur villageCoordinates: 23°08′N 91°26′E / 23.133°N 91.433°E / 23.133; 91.433Country BangladeshDivisionChittagongDistrictFeniThana1975Upazila5 November 2002Named forPhulgazi Muhammad Khan MajumdarGovernment • MP (Feni-1)Shirin Akhter • Upazila ChairmanMuhammad Abdul Alim GosaipuriArea • Total102.19 km2 (39.46 sq mi)Po...

Chinese republican revolutionary (1882–1913) In this Chinese name, the family name is Sòng (宋). Song Jiaoren宋敎仁Acting President of KuomintangIn office25 August 1912 – 22 March 1913Preceded byPosition establishedSucceeded bySun Yat-senVice President of HuaxinghuiIn office15 February 1904 – 30 July 1905Preceded byPosition establishedSucceeded byPosition abolished Personal detailsBorn(1882-04-05)5 April 1882Taoyuan, Hunan, Qing dynastyDied22 March 1913(1913-03-22) (aged 30)Sh...
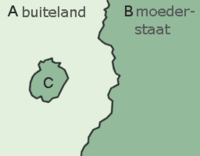
سكان A يكتنفون أو يحبسون أرض C فهي من وجهة نظرهم حبيسة، أما أهل B فإن أرضهم في C مُستحاطة. الأرض الحبيسة[1] أو المُكْتَنَفة[2] أو المحصورة[3] (بالإنجليزية: Enclave) منطقةٌ مُنفصلة عن إقليمها داخل إقليم غريب.[4][5] والأرض المستحاطة[6] أو المفصولة[7] (بالإنجل�...

Island in the river Seine, Paris, France 48°51′06″N 2°21′23″E / 48.85167°N 2.35639°E / 48.85167; 2.35639 Île Saint-Louis Île Saint-Louis (French: [il sɛ̃ lwi]), eleven hectares (27 acres) in size, is one of two natural islands in the Seine river, in Paris, France (the other natural island is the Île de la Cité, where Notre-Dame de Paris is located). Île Saint-Louis is connected to the rest of Paris by four bridges to both banks of the river a...

Work units of Nazi death camp prisoners For other uses, see Sonderkommando (disambiguation). SonderkommandoSurvivors of Sonderkommando 1005 posing next to a bone-crushing machine at the site of the Janowska concentration camp. Photograph taken following the liberation of the camp.LocationGerman-occupied EuropeDate1942–1945Incident typeRemoval of Holocaust evidencePerpetratorsSchutzstaffel (SS)ParticipantsArbeitsjudenCampExtermination camps including Auschwitz, Belzec, Chełmno, Majdanek, So...
![{\displaystyle I:=\left[0,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f216467f86655a5dab485ec2a7a248d466909665)






![{\displaystyle I^{n}=\left[0,1\right]^{n}\subset \mathbb {R} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/415ecc3184264a689d0f213efeb68bda5f6454d7)



































![{\displaystyle f,g:I\to \left[0,1\right]\times \left[0,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c64715991916bfdfbba3a7f455ea1f88dc8ad0f)








![{\displaystyle {\mathcal {R}}:=\left[-1,1\right]\times \left[-2,2\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce59a6d6d4f826940180a17275804adcfb56911e)








![{\displaystyle \left[n,s\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42015e4054f172d0c17a06d402c017b2574c7fa8)
![{\displaystyle \left[n,s\right],\,{\mathcal {G}}_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/270dcd33182fa943b18918d9f9e65b160fbedf67)
![{\displaystyle \left[n,s\right]\cap {\mathcal {G}}_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e41e6b669376772bc3bf41ad400d235855793040)



![{\displaystyle \beta \equiv \left[n,l\right]\star {\mathcal {G}}\mid _{\left[l,m\right]}\star \left[m,s\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e68cf2b3ca86187053514cb8f0b89da36ded2a5a)





![{\displaystyle \left[m,s\right]\cap {\mathcal {G}}_{s}\neq \emptyset }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d8a21b3ce4cb78a399e95eb2f6aa97681d1f906)
![{\displaystyle {\mathcal {G}}\mid _{\left[l,m\right]}\cap {\mathcal {G}}_{s}\neq \emptyset }](https://wikimedia.org/api/rest_v1/media/math/render/svg/845b01f9515d1556b13c1e60319ef988226e81e1)
![{\displaystyle \left[n,l\right]\cap {\mathcal {G}}_{s}\neq \emptyset }](https://wikimedia.org/api/rest_v1/media/math/render/svg/84bda9497a26118ba1a0e2251fe4b40d1a86f634)
![{\displaystyle x_{0}\in \left[m,p\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1050ad4c8933925b24c11e1243ab44a58e1e596)
















![{\displaystyle \left[n,l\right]\star {\mathcal {G}}\mid _{\left[l.m\right]}\star \left[m,x_{0}\right]\star \alpha \mid _{\left[x_{0},w\right]}\star {\widehat {ws}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b08db507c7f3b21046f2029561d438244b4b6a6)


![{\displaystyle {\mathcal {G}}_{s},\,\left[s,x_{0}\right]\star \alpha \mid _{\left[x_{0},m\right]}\star {\widehat {ws}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58e63629839a1641f78025e330385fd1c35487d7)





![{\displaystyle \beta \equiv \left[n,l\right]\star {\mathcal {G}}_{\left[l,m\right]}\star \left[m,p\right]\star {\mathcal {G}}_{\left[p,q\right]}\star \left[q,s\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c2226de5e7ec5f11d6f1b1d3e903c837ccc7ff8)








![{\displaystyle \left[a,a_{1}\right]\star {\widehat {a_{1}b_{1}}}\star \left[b_{1},b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6494722b062238a6eefd826982196c9fae5143f2)
