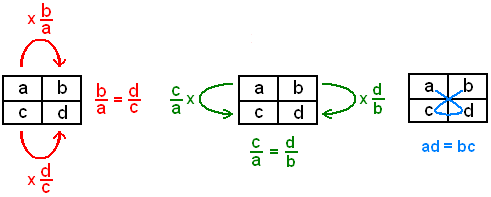
Proporcionalidade (matemáticas)
|
Read other articles:

Period of increased racism in the U.S. Nadir of American race relations1877/1890 – 1901/1923/1941 (disputed)Ku Klux Klan on parade in Springfield, Ohio in 1923.IncludingRed SummerBack-to-Africa movementGreat MigrationChronology Reconstruction era Harlem RenaissanceCivil rights movement Part of a series on theNadir of Americanrace relationsViolence in the 1906 Atlanta race massacre Historical background Reconstruction era Voter suppression Disfranchisement Redeemers Compromise of 18...

Село Ель ПальмарEl Palmar (o Lugar de Don Juan) Прапор Герб Координати 37°56′17″ пн. ш. 1°10′02″ зх. д. / 37.9382011694722223° пн. ш. 1.167368350027777835° зх. д. / 37.9382011694722223; -1.167368350027777835Координати: 37°56′17″ пн. ш. 1°10′02″ зх. д. / 37.9382011694722223° пн. ш. 1.167368350027777...

County-level city in Liaoning, People's Republic of ChinaBeizhen 北镇市County-level cityLocation in JinzhouBeizhenLocation in LiaoningCoordinates: 41°36′N 121°48′E / 41.600°N 121.800°E / 41.600; 121.800CountryPeople's Republic of ChinaProvinceLiaoningPrefecture-level cityJinzhouArea[1] • County-level city1,782.0 km2 (688.0 sq mi) • Urban78.80 km2 (30.42 sq mi)Elevation64 m (210 ft)Popula...

Plazas by the old royal palaces in Nepal This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Durbar Square – news · newspapers · books · scholar · JSTOR (August 2023) (Learn how and when to remove this template message) Patan Durbar Square in 2010 Map Durbar Square or royal Squares in English, is the generic name that refers to t...

Waitangi Geographische Lage Waitangi (Neuseeland) Koordinaten 35° 16′ S, 174° 5′ O-35.27174.081111111114Koordinaten: 35° 16′ S, 174° 5′ O Region-ISO NZ-NTL Staat Neuseeland Neuseeland Region Northland Distrikt Far North District Ward Bay of Islands-Whangaroa Ward Einwohner 39 (2013[1]) Höhe 4 m Postleitzahl 0293 Telefonvorwahl +64 (0)9 UN/LOCODE NZ WTG Webseite www.waitangi.org.nz Fotografie des Ortes Das Treaty House, Ort...

Pfarrkirche St. Josef Baujahr: 1969–1971 Lage: 49° 27′ 34,9″ N, 11° 53′ 49,3″ O49.459711.89702Koordinaten: 49° 27′ 34,9″ N, 11° 53′ 49,3″ O Anschrift: Immenstetter Straße 10, 92224 AmbergRaigeringBayern, Deutschland Zweck: römisch-katholische Kirche Gemeinde: Amberg Pfarrei: Raigering Bistum: Regensburg Die Pfarrkirche St. Josef ist ein ortsbildprägendes Kirchengebäude in Raigering, einem Ortsteil der Stadt ...

Political position in Danish government Minister of DefenceForsvarsministerenStandard of the Minister of DefenceIncumbentTroels Lund Poulsensince 22 August 2023 Ministry of DefenceMember ofthe CabinetReports tothe Prime ministerAppointerThe Monarchon advice of the Prime MinisterConstituting instrumentForsvarslovenPrecursorMinister for the NavyMinister of WarFormation14 January 1905First holderJ.C. ChristensenWebsiteOfficial Website The Minister of Defence of Denmark (Danish: Forsvarsmini...

Sailing at the Olympics Open One Person Dinghyat the Games of the XXVI OlympiadLaser (Standard Rig)VenueSavannahDates23 July to 31 JulyCompetitors56 from 56 nationsTeams56Medalists Robert Scheidt Brazil Ben Ainslie Great Britain Peer Moberg Norway2000 → Sailing at the1996 Summer OlympicsMistralmenwomenEuropewomenLaseropenFinnmen470menwomenTornadoopenStaropenSolingopenvte The Laser Competition was a sailing event on the program at the 1996 Summer Olympics...

Puerto Rican activist In this Spanish name, the first or paternal surname is López and the second or maternal family name is Rivera. Oscar López RiveraBorn (1943-01-06) January 6, 1943 (age 80)San Sebastián, Puerto RicoKnown forLongest-incarcerated FALN memberCriminal statusSentence commuted by President Obama, sentence ended in May 2017AwardsBronze Star MedalCriminal chargeSeditious conspiracy, use of force to commit robbery, interstate transportation of firearms and amm...

Le Bal des Débutantes Sesión de fotos de Vanity Fair con las debutantes de 2011LocalizaciónPaís FranciaLocalidad París, FranciaDatos generalesTipo baile de debutantes, fashion event y evento de caridadPrimera vez 1994[editar datos en Wikidata] Le Bal des Débutantes, también llamado «Le Bal» y anteriormente conocido como «Ball Crillon», es un baile de debutantes y evento de moda que se celebra en París en noviembre. Cada año participan entre 20 y 25 debutantes...

Earthquake in Switzerland 1946 Valais earthquakeRockslide at the Combe des AndinsUTC time1946-01-25 17:31:50ISC event898227USGS-ANSSComCatLocal date25 January 1946 (1946-01-25)Local time17:32 CETMagnitude6.2 MwEpicenter46°24′N 7°30′E / 46.4°N 7.5°E / 46.4; 7.5Max. intensityVIII (Severe)AftershocksThree recorded. The largest was a 5.9 Mw Casualties3 dead in Switzerland1 dead in France The 1946 Valais earthquake struck on January 25...

В Википедии есть статьи о других людях с такой фамилией, см. Михайловский; Михайловский, Николай. Николай Константинович Михайловский Портрет Н. К. Михайловского работы Н. А. Ярошенко (фрагмент) Псевдонимы Гроньяр, Посторонний, Профан Дата рождения 15 (27) ноября 184...

618 AD battle during the transition from the Sui to Tang dynasty in China Battle of YanshiPart of the transition from Sui to TangMap of the situation in China during the transition from the Sui to the Tang, with the main contenders for the throne and the main military operationsDate5–6 October 618LocationYanshi, east of Luoyang34°43′37″N 112°47′24″E / 34.727°N 112.790°E / 34.727; 112.790Result Decisive victory of Wang Shichong. Li Mi's followers join Wang...

British researcher Ailsa Jane HallOBEAlma materUniversity of BirminghamScientific careerInstitutionsUniversity of St AndrewsThesisThe health of post mortem workers : a morbidity and mortality study (1998) Ailsa Jane Hall OBE is a British researcher who is Director of the Sea Mammal Research Unit at the University of St Andrews. Her research considers the impact of contaminants on the risk of mortality in marine mammals. Early life and education In 1985, Hall joined the Universi...

A Man and a WomanNama lainHangul남과 여 Alih Aksara yang DisempurnakanNamgwa Yeo Sutradara Lee Yoon-ki Produser Oh Jung-wan Lee Dong-ha Ditulis oleh Lee Yoon-ki Sin Eun-yeong PemeranJeon Do-yeonGong YooPenata musikBang Jun-seokSinematograferKim Dong-youngPenyuntingKim Hyung-juPerusahaanproduksiBom Film ProductionsDistributorShowboxTanggal rilis 25 Februari 2016 (2016-02-25) Durasi115 menitNegara Korea Selatan Bahasa Korea PendapatankotorUS$1,5 juta[1] A Man and a W...

Запрос «CD» перенаправляется сюда; см. также другие значения. Компакт-диск Оптический носитель информации. Процесс записи и считывания информации осуществляется при помощи лазера Тип носителя оптический диск Формат контента различный Ёмкость обычно до 700 Мб (до 80 мину�...

Town in Queensland, AustraliaAlma BayQueenslandAlma Bay, 2014Alma BayCoordinates19°08′54″S 146°52′04″E / 19.1483°S 146.8677°E / -19.1483; 146.8677 (Alma Bay (town centre))Postcode(s)4819Time zoneAEST (UTC+10:00)LGA(s)City of TownsvilleState electorate(s)TownsvilleFederal division(s)Herbert Alma Bay is an island town within the locality of Arcadia on Magnetic Island in the City of Townsville, Queensland, Australia.[1] Geography The town is at...

Former South Australian weekly newspaper Not to be confused with Adelaide Chronicle and South Australian Literary Record. The Chronicle was a South Australian weekly newspaper, printed from 1858 to 1975, which evolved through a series of titles. It was printed by the publishers of The Advertiser, its content consisting largely of reprints of articles and Births, Marriages and Deaths columns from the parent newspaper. Its target demographic was country areas where mail delivery was infrequent,...

District of Erzincan Province, Turkey District in Erzincan, TurkeyOtlukbeli DistrictDistrictMap showing Otlukbeli District in Erzincan ProvinceOtlukbeli DistrictLocation in TurkeyCoordinates: 39°58′N 40°01′E / 39.967°N 40.017°E / 39.967; 40.017CountryTurkeyProvinceErzincanSeatOtlukbeliArea320 km2 (120 sq mi)Population (2021)2,577 • Density8.1/km2 (21/sq mi)Time zoneTRT (UTC+3)Websitewww.otlukbeli.gov.tr Otlukbeli District is...

جائزة بلجيكا الكبرى 1961 (بالهولندية: XXI Grote Prijs van Belgie) السباق 3 من أصل 8 في بطولة العالم لسباقات الفورمولا واحد موسم 1961 السلسلة بطولة العالم لسباقات فورمولا 1 موسم 1961 البلد بلجيكا التاريخ 18 يونيو 1961 مكان التنظيم حلبة دي سبا فرانكورشومب، حمام معدني، بلجيكا طول الم�...