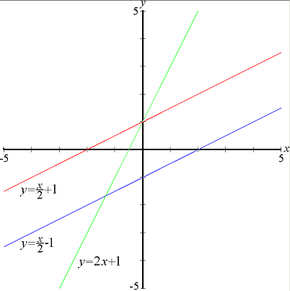
Pendente (matemáticas)
|
Read other articles:

В Википедии есть статьи о других людях с фамилией Кент. Райан Кент Общая информация Родился 11 ноября 1996(1996-11-11) (27 лет)Олдем, Англия Гражданство Англия Рост 172 см Позиция вингер Информация о клубе Клуб Фенербахче Молодёжные клубы 2003—2015 Ливерпуль Клубная карьера[* 1] 2...

Krešimir Ćosić Ćosić (n. 11) in azione alla Virtus Bologna nella stagione 1979-1980 Nazionalità Jugoslavia Altezza 209 cm Peso 94 kg Pallacanestro Ruolo CentroAllenatore Termine carriera 1983 - giocatore1992 - allenatore Hall of fame Naismith Hall of Fame (1996)FIBA Hall of Fame (2007) Carriera Giovanili 1964-1969 Zara1969-1973 BYU Cougars Squadre di club 1973-1976 Zara1976-1978 AŠK Lubiana1978-1980 Virtus Bologna1980-1983 Cibona Zagabria N...

Leluhur Raja Ælfwald dalam Textus Roffensis. Wehha muncul di baris ketujuh: Ƿehh·ƿilhelminᵹ. Wehha adalah nenek moyang legendaris dinasti Wuffinga yang memerintah Anglia Timur pada Abad Pertengahan Awal. Dia muncul dalam silsilah Koleksi Anglia sebagai putra Wilhelm dan ayahanda Wuffa, eponim dinasti Wuffinga[1]. Sebagian besar sumber menjadikan Wuffa raja pertama Anglia Timur[2], kecuali Historia Brittonum, yang mengaitkan perbedaan ini dengan Wehha. Awal pemerintahan p...

Macaco cola de cerdo sureño Estado de conservaciónVulnerable (UICN 3.1)[1]TaxonomíaReino: AnimaliaFilo: ChordataClase: MammaliaOrden: PrimatesFamilia: CercopithecidaeGénero: MacacaEspecie: M. nemestrina[2](Linnaeus, 1766)Distribución Distribución del macaco cola de cerdo sureño.[editar datos en Wikidata] El macaco cola de cerdo sureño (Macaca nemestrina) es una especie de primate catarrino de la familia Cercopithecidae. Habita en la península Malay...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) حارة وعل سليمان - حارة - تقسيم إداري البلد اليمن المحافظة محافظة صنعاء المديرية مديرية ضواح

Untuk penerus Dati II, lihat Kabupaten. Artikel ini adalah bagian dari seriPembagian administratifIndonesia Tingkat I Provinsi Daerah istimewa Daerah khusus Tingkat II Kabupaten Kota Kabupaten administrasi Kota administrasi Tingkat III Kecamatan Distrik Kapanewon Kemantren Tingkat IV Kelurahan Desa Dusun (Bungo) Gampong Kute Kalurahan Kampung Kalimantan Timur Lampung Papua Riau Lembang Nagari Nagori Negeri Maluku Maluku Tengah Negeri administratif Pekon Tiyuh Lain-lain Antara III dan IV Mukim...

Spanish philosopher (c. 1483–1546) For the bishop, see Francisco de Vitoria (bishop). Francisco de VitoriaStatue of Francisco de Vitoria at San Esteban, SalamancaBornc. 1483Burgos, Crown of CastileDied12 August 1546Salamanca, Kingdom of León, Crown of CastileEraRenaissance philosophyRegionWestern philosophy Spanish philosophy SchoolThomismSchool of SalamancaMain interestsNatural lawNotable ideasInternational lawFreedom of the seas Part of a series onCatholic philosophy Aqu...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Klasifikasi Folk adalah sistem pengelompokan gamping yang dibuat oleh Folk pada tahun 1959. Dalam klasifikasi ini, gamping dikelompokkan menjadi tiga komponen utama, yaitu alokem atau butiran, mikrit atau matriks, dan sparit atau semen. Klasifikasi Fol...

У турнірі команд другої ліги брали участь 55 команд, які були розділені на 3 групи: Група А Група Б Група В «Буковина» (Чернівці) «Верес» (Рівне) «Газовик-Скала» (Стрий) «Галичина» (Дрогобич) «Динамо» (Львів) «Закарпаття-2» (Ужгород) «Енергетик» (Бурштин) «Карпати-3» (Львів) ФК «�...

Unofficial translations made by fans Part of a series onTranslation Types Legal Literary Bible Quran Kural Linguistic validation Medical Regulatory Technical Interpretation Cultural Word-for-word Sense-for-sense Homophonic Theory Translation studies Skopos theory Translation project Translation criticism Dynamic and formal equivalence Contrastive linguistics Polysystem theory Technologies CAT Machine translation Mobile translation Translation management system Dubbing Subtitling Pre-editing P...

Illustration used to comment on current events and personalities Political cartoonComicsSpeech balloon Comics studies Education Glossary History by country Methods Cartooning Photo comics Media formats Comic book Comic strip Digital comic Gag cartoon Trade paperback Graphic novel Political cartoon Webcomic Webtoon Comics by country and culture American comics Argentine comics Australian comics Bandes dessinées (Belgium / Quebec) Brazilian comics British comics (Wales) Canadian comics Croatia...

Neighbourhood in Lahore, Punjab, PakistanHeera Mandiہیرا منڈی Shahi MohallahNeighbourhoodHeera Mandiہیرا منڈیCoordinates: 31°35′10″N 74°18′35″E / 31.586167101203753°N 74.30980680775039°E / 31.586167101203753; 74.30980680775039Country PakistanProvincePunjabCityLahoreAdministrative townRaviUnion council30 (Taxali Gate)Government Heera Mandi (Urdu and Punjabi: ہیرا منڈی, lit. 'Diamond Market'), sometimes referred to a...

Species of lizard Leopard ctenotus Ctenotus pantherinus ocellifer Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Reptilia Order: Squamata Family: Scincidae Genus: Ctenotus Species: C. pantherinus Binomial name Ctenotus pantherinus(Peters, 1866)[2][1][3] Synonyms[1][3] Lygosoma pantherinum Peters, 1866 Egernia whitei carnarae Kinghorn, 1931 Lygosoma b...

Sumatera Utara IIDaerah pemilihanuntuk Dewan Perwakilan RakyatRepublik IndonesiaWilayah Daftar Kabupaten : Humbang Hasundutan Labuhanbatu Labuhanbatu Selatan Labuhanbatu Utara Mandailing Natal Nias Nias Barat Nias Selatan Nias Utara Padang Lawas Padang Lawas Utara Tapanuli Selatan Tapanuli Tengah Tapanuli Utara Toba Samosir Kota : Gunungsitoli Padang Sidempuan Sibolga ProvinsiSumatera UtaraPopulasi4.899.018 (2020)[1]Elektorat2.630.975 (2019)[2]Daerah pemilihan saat i...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Pakuwon City Mall – berita · surat kabar · buku · cendekiawan · JSTOR Pakuwon City MallPakuwon City Mall Surabaya sebelum perluasan (saat masih bernama East Coast Center)LokasiSurabaya, IndonesiaAlamatJa...

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Bagian dari seri mengenai Sejarah Indonesia Prasejarah Manusia Jawa 1.000.000 BP Manusia Flores 94.000–12.000 BP Bencana alam Toba 75.000 BP Keb...

Artikel ini bukan mengenai Skank.Sumber referensi dari artikel ini belum dipastikan dan mungkin isinya tidak benar. Mohon periksa, kembangkan artikel ini, dan tambahkan sumber yang benar pada bagian yang diperlukan. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Gaya atau nada penulisan artikel ini tidak mengikuti gaya dan nada penulisan ensiklopedis yang diberlakukan di Wikipedia. Bantulah memperbaikinya berdasarkan panduan penulisan artikel. (Pelajari cara dan kapan saa...

Staatsliga A 1954-1955 Competizione Fußball-Bundesliga Sport Calcio Edizione 44ª Organizzatore ÖFB Date dal 28 agosto 1954al 7 luglio 1955 Luogo Austria Partecipanti 14 Cronologia della competizione 1953-54 1955-56 Manuale L'edizione 1954-55 della Staatsliga (A) vide la vittoria finale del First Vienna FC. Capocannoniere del torneo fu Richard Brousek del SC Wacker, con 31 reti. Classifica finale Classifica G V N P GF GS Pt 1 First Vienna FC 26 17 5 4 64 26 39 2 Wiener Sportcl...

American athlete, actress, and fashion model Aimee MullinsMullins in April 2008Personal informationNationalityAmericanBornAllentown, Pennsylvania, U.S.Spouse Rupert Friend (m. 2016)SportSportTrack and fieldEvent(s)Long jump, sprintingCollege teamGeorgetown UniversityAchievements and titlesParalympic finals1996 Paralympics Aimee Mullins is an American athlete, actress, and public speaker. She was born with a medical condition that resulted in the amputation of bo...

7 Seeds7SEEDS セブンシーズ(Sebun Shīzu) MangaPengarangYumi TamuraPenerbitShogakukanPenerbit bahasa IndonesiaElex Media KomputindoMajalahBetsucomi, FlowersDemografiShōjo, JoseiTerbitNovember 2001 – Juli 2017Volume35 (Daftar volume) Animasi web orisinalSutradaraYukio TakahashiSkenarioTouko MachidaStudioGonzoPelisensiNetflixTayangJuni 2019 Portal anime dan manga 7 Seeds (セブンシーズcode: ja is deprecated , Sebun Shīzu) adalah sebuah seri manga Jepang yang ditulis dan ...