Límite matemático
|
Read other articles:

Naughtysingel oleh Red Velvet - Irene & Seulgidari album mini MonsterBahasaKoreaDirilis20 Juli 2020 (2020-07-20)StudioSM, Seoul, Korea SelatanGenrefuture housepop dansaDurasi3:19Label SM Dreamus Komponis musik Moonshine Louise Frick Sveen Charite Viken Yoo Young-jin Lirikus JQ Lee Yeon-ji Kronologi singel Red Velvet - Irene & Seulgi Monster (2020) Naughty (2020) Video musikNaughty di YouTube Naughty (Hangul: 놀이; RR: Nori) adalah sebuah lagu dan singel ya...

中国電力株式会社The Chugoku Electric Power Company, Incorporated 中国電力 本社種類 株式会社市場情報 東証プライム 95041952年11月1日上場 略称 EnerGia(エネルギア)、中電、中国電本社所在地 日本〒730-8701広島県広島市中区小町4番33号設立 1951年(昭和26年)5月1日業種 電気・ガス業法人番号 4240001006753 事業内容 電力事業代表者 芦谷 茂(代表取締役会長)中川賢剛(代表取締役兼社...

The Greatest ShowmanPoster filmSutradara Michael Gracey Produser Laurence Mark Peter Chernin Jenno Topping Ditulis oleh Jenny Bicks Bill Condon Skenario Jenny Bicks Bill Condon CeritaJenny BicksPemeran Hugh Jackman Zac Efron Michelle Williams Rebecca Ferguson Zendaya Penata musik John Debney Joseph Trapanese SinematograferSeamus McGarveyPenyunting Tom Cross Robert Duffy Joe Hutshing Michael McCusker Jon Poll Spencer Susser PerusahaanproduksiChernin EntertainmentSeed ProductionsLaurence ...
Annual blues festival held in Jacksonville Beach, Florida Springing the Blues FestivalGenreBluesLocation(s)Jacksonville Beach, FloridaYears active1990–presentWebsiteSpringing the Blues Springing the Blues is an annual blues festival held in Jacksonville Beach, Florida. It is one of the largest and oldest blues festivals on the East Coast of the United States.[1] It was first held in 1990 and has been held yearly on the first weekend of April.[2] History The first Springing t...

1955 soundtrack album by castOklahoma!Soundtrack album by castReleasedAugust 1, 1955 (1955-08-01)RecordedMay 11, 1955GenreSoundtrackLabelAngelProducerAndy McKaie, Ron OBrien Professional ratingsReview scoresSourceRatingAllmusic[1] Oklahoma! is the original soundtrack album of the 1955 film Oklahoma!, an adaptation of the musical Broadway play of the same name. The soundtrack charted No. 1 on the Billboard Pop Album Chart in 1956 and has been in continual print. ...

1998 single by Human NatureCruelSingle by Human Naturefrom the album Counting Down B-sideWithout YouReleasedAugust 1998Recorded1998GenrePopLength4:11LabelSony Music Records, Columbia RecordsSongwriter(s)Andrew Klippel, Shep SolomonProducer(s)Andrew KippelHuman Nature singles chronology People Get Ready (1996) Cruel (1998) Last to Know (1999) Music videoCruel on YouTube Cruel is a song by Human Nature, released as the lead single from their album second studio album Counting Down. The song pea...

Gemeinde Polop Wappen Karte von Spanien Polop (Spanien) Basisdaten Land: Spanien Spanien Autonome Gemeinschaft: Valencia Valencia Provinz: Alicante Comarca: Marina Baixa Gerichtsbezirk: Villajoyosa Koordinaten 38° 37′ N, 0° 8′ W38.622-0.127262Koordinaten: 38° 37′ N, 0° 8′ W Höhe: 262 msnm Fläche: 22,58 km² Einwohner: 5.186 (1. Jan. 2022)[1] Bevölkerungsdichte: 230 Einw./km² Postleitzahl(en): 03520 Gemeindenum...

Abraham O. SmootPhoto of A. O. Smoot by C. R. SavageBornAbraham Owen Smoot(1815-02-17)February 17, 1815Owenton, KentuckyDiedMarch 6, 1895(1895-03-06) (aged 80)Provo, Utah TerritoryMonumentsSmoot Administration Building, Brigham Young UniversityNationalityAmericanTitleMayor of Salt Lake City, Utah; Mayor of Provo, UtahTerm1857-1866; 1868-1881PredecessorJedediah M. GrantSuccessorDaniel H. WellsSpouses Margaret Thompson McMeans Sarah Gibbens Emily Hill Diana Caroline Tanner Eldredge Anne Ki...

Marian apparition that occurred in Zeitoun, a district of Cairo, Egypt, beginning in 1968 Our Lady of ZeitounAn alleged photo of the Virgin Mary above the Church of Virgin Mary in Zeitoun, CairoLocationZeitoun, Cairo, EgyptDate2 April 1968TypeMarian apparitionApproval4 May 1968, Canonically granted by Pope Kyrillos VIVenerated inOriental OrthodoxyShrineChurch of the Virgin Mary, Zeitoun, Cairo, EgyptPatronageEgyptAttributesVirgin Mary dressed in white, dove on her head, holding an olive branc...

Parte da série sobrePolítica do Kosovo Constituição Executivo Presidente - Vjosa Osmani Primeiro-ministro - Albin Kurti Legislativo Assembleia do Kosovo Judiciário Tribunal Constitucional Eleições Eleições parlamentares - 2019 · 2021 Eleições presidenciais - 2016 · 2021 Partidos políticos Tópicos relacionados Subdivisões regionais Relações internacionais Independência do Kosovo Portal do Kosovovde Ver também vdePredefinições de política da Euro...

Ethnic group in Chicago This article's use of red links may need cleanup. Please help improve this article. (November 2023) Part of a series onEthnic groups in Chicago Armenians Afghans African Americans Albanians Appalachian Assyrians Austrians Belarusians Belgians Bosnians Brazilians Chinese Croatians Czechs Dutch English Estonians Finns Germans Ghanaians Guatemalans Greeks Iranians Iraqi Irish Indians Italians Japanese Jews Koreans Latvians Lithuanians Luxembourgers Mexicans Native peoples...

Filipina musician This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Lou Bonnevie – news · newspapers · books · scholar · JSTOR (September 2013) (Learn how and when to remove this template message)...

本来の表記は「近衞忠熈」です。この記事に付けられたページ名は技術的な制限または記事名の制約により不正確なものとなっています。 凡例近衞忠熈 近衛忠熙時代 江戸時代後期 - 明治時代生誕 文化5年7月14日(1808年9月4日)死没 明治31年(1898年)3月18日(89歳没)別名 号:翠山官位 従一位、関白、左大臣、贈正一位主君 光格天皇→仁孝天皇→孝明天皇→明治天...

Artikel ini bukan mengenai TVRI (saluran televisi), saluran utama TVRI yang dahulu juga dikenal sebagai TVRI Stasiun Pusat Jakarta. TVRI JakartaLPP TVRI Stasiun JakartaKantor pusat LPP TVRI di Jakarta Pusat, yang juga menjadi kantor TVRI JakartaJakarta Pusat, DKI JakartaIndonesiaSaluranDigital: 43 UHF (DVB-T2) (multipleks TVRI Joglo)Virtual: 2SloganMedia Pemersatu BangsaPemrogramanBahasaBahasa IndonesiaBahasa BetawiAfiliasiTVRI, SEA Today & ANTARA TVKepemilikanPemilikLPP TVRIRiwayatSiaran...

Global article on the first meal of the day Breakfast, the first meal of the day eaten after waking from the night's sleep, varies in composition and tradition across the world. Africa Breakfast in Africa varies greatly from region to region.[1] Algeria Due to Algeria's history of having been a colony of France, breakfast in Algeria is heavily influenced by French cuisine and most commonly consists of café au lait or espresso along with a sweet pastry (some common examples are croiss...

Israeli psychoneuroimmunologist Asya RollsAsya Rolls in 2020BornRussiaNationalityIsraeliAlma materThe Hebrew Reali School in Haifa, IsraelIsrael Institute of TechnologyWeizmann InstituteStanford UniversityKnown forBrain representation and control of immunity and cancerScientific careerFieldsNeuroimmunologyInstitutionsIsrael Institute of TechnologyDoctoral advisorMichal Schwartz[1] Ofer Lider[1] Websiterolls.net.technion.ac.il Asya Rolls is an Israeli psychoneuroimmun...

بطولة ويمبلدون 1982 جزء من بطولة ويمبلدون رقم الفعالية 96 البلد المملكة المتحدة التاريخ 1982 الرياضة كرة المضرب الفعاليات بطولة ويمبلدون 1982 - فردي السيدات، وبطولة ويمبلدون 1982 - فردي الرجال، وبطولة ويمبلدون 1982 - زوجي السيدات، وبطولة ويمبلدون 1982 – زوجي �...
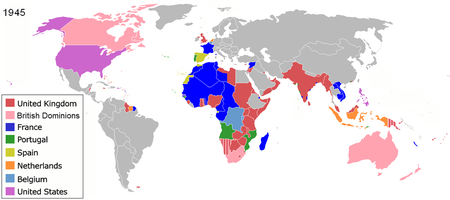
Dieser Artikel oder nachfolgende Abschnitt ist nicht hinreichend mit Belegen (beispielsweise Einzelnachweisen) ausgestattet. Angaben ohne ausreichenden Beleg könnten demnächst entfernt werden. Bitte hilf Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. der längere und durchaus kontrovers/fragwürdig zu sehende Aussagen enthaltende Text belegt lediglich 2 Einzelfakten. andy_king50 (Diskussion) 15:37, 1. Nov. 2018 (CET) Kolonialmächte und Kolonialgebiete 1945 Unter D...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Shandhika Widya Cinema – berita · surat kabar · buku · cendekiawan · JSTOR Shandhika Widya CinemaJenisPerusahaan swastaIndustriInfotainmenDidirikan12 Mei 1995 (1995-05-12)KantorpusatJalan Media Masa...

Lithuanian footballer This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Marius Stankevičius – news · newspapers · books · scholar · JSTOR (May 2016) (Learn how and when to remove this template me...




























![{\displaystyle \lim _{t\rightarrow 0}{\frac {t}{t^{2}}}={\frac {0}{0}}\quad {\xrightarrow[{\mathrm {simplificando} }]{}}\quad \lim _{t\rightarrow 0}{\frac {1}{t}}=\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f51283b47926fd84240f1abc028fa6736f61586)
![{\displaystyle \lim _{t\rightarrow 0}{\frac {t}{t}}={\frac {0}{0}}\quad {\xrightarrow[{\mathrm {simplificando} }]{}}\quad \lim _{t\rightarrow 0}1=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc419c7d15ef086ea702d25f152ffcaf8c085989)
![{\displaystyle \lim _{t\rightarrow 0}{\frac {t^{2}}{t}}={\frac {0}{0}}\quad {\xrightarrow[{\mathrm {simplificando} }]{}}\quad \lim _{t\rightarrow 0}{t}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a6d4d40fe3877905357364e193a873646aca799)
