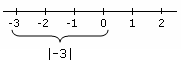Desigualdade (matemáticas)
|
Read other articles:

اضغط هنا للاطلاع على كيفية قراءة التصنيف أسرة الموتيسياوات الجربارة المرتبة التصنيفية فصيلة فرعية التصنيف العلمي النطاق: حقيقيات النوى المملكة: النباتات الفرقة العليا: نباتات جنينية القسم: نباتات وعائية الشعبة: حقيقيات الأوراق الشعيبة: بذريات العمارة: كاسيات البذور ال

Su-25UT / Su-28 Un Su-28. Tipo Avión de entrenamientoFabricante SukhoiPrimer vuelo 1987Usuario principal Fuerza Aérea RusaDesarrollo del Sukhoi Su-25[editar datos en Wikidata] El Sukhoi Su-28 (en ruso: Сухой Су-28), también conocido como Su-25UT (Uchebno-Trenirovochnyy) es un avión de entrenamiento, derivado del Sukhoi Su-25UB, surgido como una iniciativa privada del fabricante ruso Sukhoi. El Su-28 nació como una propuesta para reempazar al Aero L-39 Albatros. Al contra...

Orthodoxe icoon van Maria van Egypte Maria van Egypte (ca. 344 – ca. 421) is een heilig persoon uit het christendom. Ze wordt vereerd als de patroonheilige van vrouwen die boete doen, vooral in de oriëntaals orthodoxe kerken, oosters- orthodoxe en oosters-katholieke kerken, in de Rooms-Katholieke en Anglicaanse Kerk. Vita S. Maria Aegyptiaca De belangrijkste bron over het leven van Maria van Egypte is de Vita S. Maria Aegyptiaca (Latijn voor: levensbeschrijving van de heilige Maria van Egy...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Dear Friend HitlerPoster rilis teatrikalSutradaraRakesh Ranjan Kumar[1]Produser Dr. Anil Kumar Sharma Ditulis oleh Rakesh Ranjan Kumar SkenarioRakesh Ranjan KumarCeritaNalin SinghRakesh Ranjan KumarRutvik OzaPemeranRaghubir YadavNeha DhupiaAma...

1973 studio album by Jimmy HeathLove and UnderstandingStudio album by Jimmy HeathReleased1973RecordedJune 11, 1973RCA Studios, New York CityGenreJazzLength38:03LabelMuseMR 5028ProducerDon SchlittenJimmy Heath chronology The Gap Sealer(1972) Love and Understanding(1973) The Time and the Place(1974) Love and Understanding is an album by saxophonist Jimmy Heath featuring performances recorded in 1973 and originally released on the Muse label.[1][2] Reception Professional ...

French sports newspaper For other uses, see Équipe (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: L'Équipe – news · newspapers · books · scholar · JSTOR (July 2008) (Learn how and when to remove this template message) L'ÉquipeThe front page of L'Équipe on 4 July 2011TypeDaily newspaper...

Dutch chess player (1862–1956) In this Dutch name, the surname is van Foreest, not Foreest. Dirk van ForeestCountryNetherlandsBorn3 May 1862Haarlemmermeer, NetherlandsDied24 February 1956 (1956-02-25) (aged 93)Oosthuizen, Netherlands Jonkheer Dirk van Foreest (3 May 1862 – 24 February 1956) was a Dutch chess master.[1] The elder brother of Arnold van Foreest, he thrice won Dutch Championship (in 1885, 1886, and 1887).[2] He also took fifth place in 1884 and took ...

Assemblage of Upper Triassic and Lower Jurassic sedimentary rocks Newark SupergroupStratigraphic range: Triassic - JurassicExposed basins of the Newark SupergroupTypeSupergroupSub-unitssee textLocationRegionEast Coast, The Maritime ProvincesCountry United States, CanadaExtentNova Scotia, New Brunswick, Massachusetts, Connecticut, New York, New Jersey, Pennsylvania, Maryland, Virginia, North Carolina, and South CarolinaType sectionNamed forNewark, New Jersey The Newark Supergroup, a...

Part of the Syrian civil war spillover in Lebanon Battle of Sidon redirects here. For the World War II battle, see Battle of Sidon (1941). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 2013 Sidon clash – news · newspapers · books · scholar · JSTOR (September 2013) (Learn how and when to remove this templat...

Азербайджанці в Ірані(İran azərbaycanlıları; آذربایجانیهای ایران)Кількість від15 до 30 мільйонівРаса Європеоїдна раса (Каспійський підтип)Близькі до: ТюркиМова АзербайджанськаРелігія Більшість мусульмани-шиїти[1]; меншість складають мусульмани-суніти[2]. Азербайджанці в...

Manga series by Seita Horio Kokkoku: Moment by MomentCover of the first manga volume刻刻(Kokkoku)GenreMystery[1]Science fiction[1]Supernatural thriller[1] MangaWritten bySeita HorioPublished byKodanshaEnglish publisherNA: Kodansha USA (digital)MagazineMonthly Morning TwoDemographicSeinenOriginal run22 May 2008 – 22 September 2014Volumes8 Anime television seriesDirected byYoshimitsu ŌhashiProduced byMakoto KimuraWritten byNoboru KimuraMusic...

This article is about the song. For the Andrew Lloyd Webber musical, see Cinderella (Lloyd Webber musical). 2020 single by Carrie Hope FletcherBad CinderellaSingle by Carrie Hope Fletcherfrom the album Andrew Lloyd Webber's Cinderella Released30 October 2020Recorded2020LabelPolydorComposer(s)Andrew Lloyd WebberLyricist(s)Andrew Lloyd WebberDavid ZippelProducer(s)Andrew Lloyd WebberGreg WellsMusic videoBad Cinderella (West End version) on YouTube Bad Cinderella is a song from Andrew Lloyd Webb...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Transvaal Agricultural Union – news · newspapers · books · scholar · JSTOR (January 2017) (Learn how and wh...

The Tower Glen Howe Park is a public recreation area in the village of Wharncliffe Side within the City of Sheffield, England. The park covers an area of 19 acres in the valley of the Tinker Brook, a minor tributary of the River Don. It is home to a variety of fungi, rare plants and animals only found in ancient woodlands. History The valley of the Tinker Brook first became colonised by trees after the last ice age and has remained wooded ever since. The Tinker Brook and Howe Wood were first ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Alexians – news · newspapers · books · scholar · JSTOR (July 2018) (Learn how and when to remove this template message) Congregation of Alexian BrothersCongregatio Fratrum Cellitarum seu AlexianorumAlexians monastery in Ghent (Belgium) on the former Oude Houtle...

Crime is present in various forms in Myanmar (also known as Burma) and is continuous with the activities of many drug trafficking financed militias at the eastern and western border regions, and with corruption within and challenges to the central government. Crime by type Murder Further information: List of countries by intentional homicide rate In 2012, Burma had a murder rate of 15.2 per 100,000 population.[1] There were a total of 8,044 murders in Burma in 2012.[1] Factors...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مايو 2022) إينيغو أرتيجا معلومات شخصية الميلاد 16 ديسمبر 1972 (العمر 51 سنة)سان سيباستيان الطول 1.85 م (6 قدم 1 بوصة) مركز اللعب حارس مرمى الجنسية إسبانيا مسيرة ال�...
Chronologies Données clés 2011 2012 2013 2014 2015 2016 2017Décennies :1980 1990 2000 2010 2020 2030 2040Siècles :XIXe XXe XXIe XXIIe XXIIIeMillénaires :Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, République centrafricaine, Comores, République du Congo, République démocratique du Congo, Côte d'Ivoire, Djibouti, Égypte, �...

Plant used for food, medicine or perfume This article is about culinary, medicinal, and spiritual herbs. For the botanical usage, see herbaceous plant. For other uses, see Herb (disambiguation). A variety of herbs are visible in this garden, including mint. In general use, herbs are a widely distributed and widespread group of plants, excluding vegetables and other plants consumed for macronutrients, with savory or aromatic properties that are used for flavoring and garnishing food, for medic...

Marchio del concorso Il Totip, abbreviazione di totalizzatore ippico, è stato un concorso a premi il cui obiettivo consisteva nella previsione dell'esito di varie corse di cavalli. Nato nel secondo dopoguerra, il gioco ebbe notevole popolarità sino agli anni ottanta, per poi progressivamente perdere d'interesse, sino alla sua chiusura nel 2007.[1] Indice 1 Storia 1.1 L'abbinamento al Festival di Sanremo per la selezione del vincitore (1983 - 1989) 2 Record 3 Note 4 Voci correlate 5 ...