 Ų
ØŊŲ ØŠØąÚĐÛØĻÛ
Ų
ØŊŲ ØŠØąÚĐÛØĻÛ
Ų
ØŊŲ ØŠØąÚĐÛØĻÛ Ûا Ų
ØŊŲ Ų
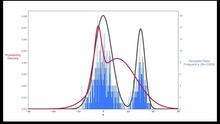
ØŪŲŲØ· (ØĻŲ اŲÚŊŲÛØģÛ: Mixture Model): ØŊØą ØĒŲ
Ø§ØąØ ÛÚĐ Ų
ØŊŲ ØŠØąÚĐÛØĻÛØ ŲŲ
اÛØī اØØŠŲ
اŲÛ ÛÚĐ ØŽŲ
ØđÛØŠ اØģØŠ ÚĐŲ ØØķŲØą ØēÛØąØŽŲ
ØđÛØŠâŲØ§Û Ų
ØŪØŠŲŲ ØąØ§ ØŊØą ØĒŲ ŲØīاŲ Ų
ÛâØŊŲØŊ. ØĻØą ØŪŲاŲ Ų
ØŊŲâŲØ§Û ØģŲØŠÛØ Ų
ØŊŲâŲØ§Û Ų
ØŪŲŲØ· ŲÛاØēÛ ØĻŲ ØŠØŪØĩÛØĩ Ų
ØīاŲØŊا؊ ŲØąØŊÛ ØĻŲ ÛÚĐ ØēÛØąØŽŲ
ØđÛØŠ ØŪاØĩ ŲØŊØ§ØąŲØŊ. ØŊØą ØđŲØķØ ØĒŲŲا ØŠŲØēÛØđ اØØŠŲ
اŲ Ų
ØīاŲØŊا؊ ØąØ§ ØŊØą ÚĐŲ ØŽŲ
ØđÛØŠ ØŠŲØĩÛŲ Ų
Û ÚĐŲŲØŊ. Ų
ØŊŲâŲØ§Û Ų
ØŪŲŲØ· اŲ
ÚĐاŲ اØģØŠŲ؊ا؎âŲØ§Û ØĒŲ
Ø§ØąÛ ØŊØą Ų
ŲØąØŊ ŲÛÚÚŊÛâŲØ§Û ØēÛØąØŽŲ
ØđÛØŠâŲا ØąØ§ ØŠŲŲا ØĻØą اØģاØģ Ų
ØīاŲØŊا؊ ÚĐŲ ØŽŲ
ØđÛØŠØ ØĻØŊŲŲ ŲÛÚ ÚŊŲŲŲ اطŲاØđØ§ØŠÛ ØŊØą Ų
ŲØąØŊ ŲŲÛØŠâŲØ§Û ØēÛØąØŽŲ
ØđÛØŠÛ ŲØąØ§ŲŲ
Ų
ÛâÚĐŲŲØŊ.[Ûą]
ØģاØŪØŠØ§Øą
Ų
ØŊŲ ØŠØąÚĐÛØĻÛ ØđŲ
ŲŲ
Û
ÛÚĐ Ų
ØŊŲ ØŠØąÚĐÛØĻÛ ØĻا اØĻØđاØŊ Ų
ØØŊŲØŊ ÛÚĐ Ų
ØŊŲ ØģŲØģŲŲ Ų
ØąØ§ØŠØĻÛ Ø§ØģØŠ ÚĐŲ اØē ا؎ØēØ§Û ØēÛØą ØŠØīÚĐÛŲ ØīØŊŲ اØģØŠ:
N Ų
ØŠØšÛØą ØŠØĩاØŊŲÛ ÚĐŲ Ų
ØīاŲØŊŲ ØīØŊŲâاŲØŊ Ų ŲØą ÚĐØŊاŲ
ØĻØą اØģاØģ ØŠØąÚĐÛØĻÛ Ø§Øē Ų
ØĪŲŲŲâŲØ§Û K ØŠŲØēÛØđ Ų
ÛâØīŲŲØŊ.
N Ų
ØŠØšÛØą ŲŲŲØŠŲ ØŠØĩاØŊŲÛ ÚĐŲ ا؎ØēØ§Û ØŠØąÚĐÛØĻÛ ŲØą Ų
ØīاŲØŊŲ ØąØ§ Ų
ØīØŪØĩ Ų
ÛâÚĐŲØŊØ ÚĐŲ ŲØą ÚĐØŊاŲ
ØĻØą اØģاØģ ÛÚĐ ØŠŲØēÛØđ Ø·ØĻŲŲ ØĻŲØŊÛ K ØĻØđØŊÛ ØŠŲØēÛØđ ØīØŊŲ اŲØŊ.
Ų
ØŽŲ
ŲØđŲ Ø§Û Ø§Øē ŲØēŲ ŲØ§Û ØŠØąÚĐÛØĻÛ K؊اÛÛØ ÚĐŲ اØØŠŲ
اŲØ§ØŠÛ ŲØģØŠŲØŊ ÚĐŲ Ų
ØŽŲ
ŲØđ ØĒŲŲا 1 اØģØŠ.
Ų
ØŽŲ
ŲØđŲ Ø§Û Ø§Øē ŲūØ§ØąØ§Ų
ØŠØąŲØ§Û K؊اÛÛ ÚĐŲ ŲØą ÚĐØŊاŲ
ŲūØ§ØąØ§Ų
ØŠØąŲØ§Û Ų
ØąØĻŲØ· ØĻŲ ØŠŲØēÛØđ Ų
ØąØĻŲØ·Ų ØąØ§ Ų
ØīØŪØĩ Ų
Û ÚĐŲØŊ.
Ų
ØŊŲ ØŠØąÚĐÛØĻÛ ÚŊاŲØģÛ
ÛÚĐ ØąŲØī Ų
ØŠØŊاŲŲ ØŊØą ØŪŲØīŲâØĻŲØŊÛ ØŊØą ÛاØŊÚŊÛØąÛ Ų
اØīÛŲØ Ø§ØģØŠŲاØŊŲ اØē Ų
ØŊŲ ØĒŲ
ÛØŪØŠŲ ÚŊŲØģÛ Ûا ŲØąŲ
اŲ اØģØŠ. ØŊØą اÛŲ ØąŲØīØ ŲØąØķ Ų
ÛâØīŲØŊ ÚĐŲ ŲØą ØŪŲØīŲ اØē ØŊاØŊŲâŲا ØĻŲ ØīÚĐŲÛ ŲØąŲ
اŲ (ÚŊŲØģÛ) ØŠŲØēÛØđ ØīØŊŲ اØģØŠ Ų ØĻŲ Ø·ŲØą ÚĐŲÛØ ØŊاØŊŲâŲا ŲŲ
ŲŲŲâŲاÛÛ Ø§Øē ÛÚĐ ØŠŲØēÛØđ ØĒŲ
ÛØŪØŠŲ ŲØąŲ
اŲ ŲØģØŠŲØŊ. ŲØŊŲ اØē ØŪŲØīŲâØĻŲØŊÛ ØĻØąŲ
ØĻŲØ§Û Ų
ØŊŲØ ØĻØąØĒŲØąØŊ ŲūØ§ØąØ§Ų
ØŠØąŲØ§Û ØŠŲØēÛØđ ŲØą ØŪŲØīŲ Ų ØŠØđÛÛŲ ØĻØąÚØģØĻ ØĻØąØ§Û Ų
ØīاŲØŊا؊ اØģØŠ. ØĻا اØģØŠŲاØŊŲ اØē اÛŲ ØąŲØīØ Ų
ÛâØŠŲاŲÛŲ
ØĻŲŲŲ
ÛŲ
ŲØą Ų
ØīاŲØŊŲ ØĻŲ ÚĐØŊاŲ
ØŪŲØīŲ ØŠØđŲŲ ØŊØ§ØąØŊ. ØąŲØī ØŪŲØīŲâØĻŲØŊÛ ØĻØąŲ
ØĻŲØ§Û Ų
ØŊŲ ÛÚĐ ØąŲØī ŲØŊØąØŠŲ
ŲØŊ ØŊØą ØŲØēŲ ÛاØŊÚŊÛØąÛ Ų
اØīÛŲ اØģØŠ.
ØŊØą ØīÛŲŲ ØŪŲØīŲâØĻŲØŊÛ ØĻا Ų
ØŊŲ ØĒŲ
ÛØŪØŠŲ ÚŊاŲØģÛØ ØĻØąØĒŲØąØŊ ŲūØ§ØąØ§Ų
ØŠØąŲØ§Û ØŠŲØēÛØđ ØĒŲ
ÛØŪØŠŲ اØē ÛÚĐ Ų
ØŠØšÛØą ŲūŲŲاŲ (ØĻŲ اŲÚŊŲÛØģÛ: Latent Variable) اØģØŠŲاØŊŲ Ų
ÛâØīŲØŊ. ØĻŲ اÛŲ ØŠØąØŠÛØĻ ØĻŲ ÚĐŲ
ÚĐ Ø§ŲÚŊŲØąÛØŠŲ
(EM (Expectation Maximization Ų
ÛâØŠŲاŲ ØĻØąØĒŲØąØŊ Ų
ŲاØģØĻ ØĻØąØ§Û ŲūØ§ØąØ§Ų
ØŠØąŲا Ų Ų
ŲØŊØ§Øą Ų
ØŠØšÛØą ŲūŲŲاŲ ØĻŲ ØŊØģØŠ ØĒŲØąØŊ.
ÛÚĐ Ų
ØŊŲ ØŠØąÚĐÛØĻÛ ÚŊاŲØģÛ ØĻÛØēÛ Ø§ØšŲØĻ ØĻØģØ· ŲūÛØŊا Ų
ÛâÚĐŲØŊ ؊ا Ų
ØŽŲ
ŲØđŲâØ§Û Ø§Øē ŲūØ§ØąØ§Ų
ØŠØąŲØ§Û ŲاŲ
ØđŲŲŲ
Ûا ØŠŲØēÛØđâŲØ§Û ŲØąŲ
اŲ ÚŲØŊ Ų
ØŠØšÛØąŲ ØąØ§ ØŊØą ØŪŲØŊ ØŽØ§Û ØŊŲØŊ. ØŊØą Ų
ŲØąØŊ ØŠŲØēÛØđ ÚŲØŊ Ų
ØŠØšÛØąŲ (ÛØđŲÛ ØŠŲØēÛØđÛ ÚĐŲ ØĻØąØŊØ§Øą x ØąØ§ ØĻا N Ų
ØŠØšÛØą ØŠØĩاØŊŲÛ Ų
ØŊŲ Ų
ÛâÚĐŲØŊ)Ø Ų
ÛâØŠŲاŲ Ų
ØŽŲ
ŲØđŲâØ§Û Ø§Øē ŲūØ§ØąØ§Ų
ØŠØąŲا ØąØ§ ØĻا اØģØŠŲاØŊŲ اØē ØŠŲØēÛØđ ŲØĻŲÛ(prior) ÛÚĐ ÚŊاŲØģÛ ØŠØąÚĐÛØĻÛ ØĻØą ØąŲÛ ØĻØąØŊØ§Øą Ų
ŲاØŊÛØą ØŠØŪŲ
ÛŲÛ Ø§ØąØ§ØĶŲ ØīØŊŲ ØŠŲØģØ· Ų
ØŊŲ ŲØīاŲ ØŊاØŊ.

ÚĐŲ ØŊØą اÛŲ؎ا ØŽØēØĄ iاŲ
ØĻŲ ØĩŲØąØŠ ØŠŲØēÛØđ ŲØ§Û ŲØąŲ
اŲ ØĻا ŲØēŲâŲØ§Û  Ø Ų
ÛاÚŊÛŲâŲاÛ
Ø Ų
ÛاÚŊÛŲâŲØ§Û  Ų Ų
Ø§ØŠØąÛØģ ÚĐŲØ§ØąÛاŲØģ
Ų Ų
Ø§ØŠØąÛØģ ÚĐŲØ§ØąÛاŲØģ  Ų
ØīØŪØĩ Ų
ÛâØīŲŲØŊ.
Ų
ØīØŪØĩ Ų
ÛâØīŲŲØŊ.
ØģŲūØģ Ų
ÛâØŠŲاŲ ØĻا اØģØŠŲاØŊŲ اØē ŲØąŲ
ŲŲ ØĻÛØē ØŠŲØēÛØđ ŲūÛØīÛŲ ØąØ§ ØŊØą ØŠŲØēÛØđ  ØķØąØĻ ÚĐØąØŊ Ų ØŠŲØēÛØđ ŲūØģÛŲ ØĻØŊØģØŠ Ų
ÛâØĒÛØŊ.
ØķØąØĻ ÚĐØąØŊ Ų ØŠŲØēÛØđ ŲūØģÛŲ ØĻØŊØģØŠ Ų
ÛâØĒÛØŊ.
 Ų ŲūØ§ØąØ§Ų
ØŠØąŲØ§Û ŲØēŲâŲØ§Ø Ų
ÛاÚŊÛŲâŲا Ų Ų
Ø§ØŠØąÛØģ ÚĐŲØ§ØąÛاŲØģ ØŠŲØģØ· اŲÚŊŲØąÛØŠŲ
EM ØĻŲâØąŲØēØąØģاŲÛ ØŪŲاŲŲØŊ ØīØŊ.[Ûē]
Ų ŲūØ§ØąØ§Ų
ØŠØąŲØ§Û ŲØēŲâŲØ§Ø Ų
ÛاÚŊÛŲâŲا Ų Ų
Ø§ØŠØąÛØģ ÚĐŲØ§ØąÛاŲØģ ØŠŲØģØ· اŲÚŊŲØąÛØŠŲ
EM ØĻŲâØąŲØēØąØģاŲÛ ØŪŲاŲŲØŊ ØīØŊ.[Ûē]
اŲÚŊŲØąÛØŠŲ
EM
ØĻŲ Ų
ŲØļŲØą ØĻØąØĒŲØąØŊ ŲūØ§ØąØ§Ų
ØŠØąŲØ§Û Ų
ØŊŲ ØĒŲ
ÛØŪØŠŲ ÚŊاŲØģÛ Ø§Øē اŲÚŊŲØąÛØŠŲ
EM اØģØŠŲاØŊŲ ØŪŲاŲÛŲ
ÚĐØąØŊ. اÛŲ اŲÚŊŲØąÛØŠŲ
ØŊØ§ØąØ§Û ØŊŲ ØĻØŪØī Ûا ÚŊاŲ
اØģØŠ. ÚŊاŲ
Ų
ØŠŲØģØ· ÚŊÛØąÛ Ûا Expectation Ų ÚŊاŲ
ØĻÛØīÛŲŲâØģاØēÛ Ûا Maximization.
ØŊØą ÚŊاŲ
اŲŲ (E-step) Ûا ÚŊاŲ
Ų
ØŠŲØģØ·âÚŊÛØąÛØ ŲØŊŲ ØĻØąØĒŲØąØŊ ØŠŲØēÛØđ Ų
ØŠØšÛØą ŲūŲŲاŲ ØĻŲ ØīØąØ· ŲØēŲ (Ï)Ø Ų
ÛاŲÚŊÛŲâŲا (Means) Ų Ų
Ø§ØŠØąÛØģ ÚĐŲØ§ØąÛاŲØģ (ÎĢ) ØŠŲØēÛØđ ØĒŲ
ÛØŪØŠŲ ŲØąŲ
اŲ اØģØŠ. ØĻØąØŊØ§Øą ŲūØ§ØąØ§Ų
ØŠØąŲا ØąØ§ ØŊØą اÛŲ ؎ا ØĻا ŲŲ
اØŊ Îļ ŲØīاŲ Ų
ÛâØŊŲÛŲ
. ØĻØąØ§Û Ø§ÛŲ ÚĐØ§Øą اØĻØŠØŊا ÛÚĐ ØØŊØģ اŲŲÛŲ ØĻØąØ§Û Ø§ÛŲ ŲūØ§ØąØ§Ų
ØŠØąŲا ØēØŊŲ Ų
ÛâØīŲØŊ ØģŲūØģ ÚŊاŲ
âŲØ§Û ØĻŲ ØŠØąØŠÛØĻ ØĻØąØŊاØīØŠŲ Ų
ÛâØīŲŲØŊ. ŲŲ
اŲØ·ŲØą ÚĐŲ ØŪŲاŲÛØŊ ØŊÛØŊØ ØØŊØģâŲØ§Û Ø§ŲŲÛŲ ØąØ§ Ų
ÛâØŠŲاŲ ØĻŲØģÛŲŲ اŲÚŊŲØąÛØŠŲ
k means ØĻØŊØģØŠ ØĒŲØąØŊ. ØĻŲ اÛŲ Ų
ØđŲÛ ÚĐŲ ØĻØąØ§Û ØŪŲØīŲâŲØ§Û ØاØĩŲ اØē اŲÚŊŲØąÛØŠŲ
k meansØ Ų
ÛاŲÚŊÛŲØ Ų
Ø§ØŠØąÛØģ ÚĐŲØ§ØąÛاŲØģ Ų ŲØēŲâŲا Ų
ØاØģØĻŲ Ų
ÛâØīŲØŊ. ØŠŲØŽŲ ØŊاØīØŠŲ ØĻاØīÛØŊ ÚĐŲ Ų
ŲØļŲØą اØē ŲØēŲØ ØŊØąØĩØŊÛ (اØØŠŲ
اŲ) اØē ØŊاØŊŲâŲا اØģØŠ ÚĐŲ ØŊØą ÛÚĐ ØŪŲØīŲ ŲØąØ§Øą ØŊØ§ØąŲØŊ.
ØŊØą ÚŊاŲ
ØŊŲŲ
(M-step) ØĻا اØģØŠŲاØŊŲ اØē Ų
ØŠØšÛØąŲØ§Û ŲūŲŲاŲØ ØģØđÛ ØŪŲاŲÛŲ
ÚĐØąØŊ ؊اØĻØđ ØŊØąØģØŠŲŲ
اÛÛ ØąØ§ ŲØģØĻØŠ ØĻŲ ŲūØ§ØąØ§Ų
ØŠØąŲØ§Û Îļ ØĻÛØīÛŲŲ ÚĐŲÛŲ
. اÛŲ Ų
ØąØ§ØŲ (ÚŊاŲ
E Ų ÚŊاŲ
M) ؊ا ØēŲ
اŲÛ ÚĐŲ اŲÚŊŲØąÛØŠŲ
ŲŲ
ÚŊØąØ§ ØīŲØŊ (Ų
ŲØŊØ§Øą ؊اØĻØđ ØŊØąØģØŠŲŲ
اÛÛ ØŠØšÛÛØą ŲÚĐŲØŊ)Ø Ø§ØŊاŲ
Ų ØŪŲاŲØŊ ØŊاØīØŠ. ØĻŲ اÛŲ ØŠØąØŠÛØĻ اŲÚŊŲØąÛØŠŲ
EM ØđŲاŲŲ ØĻØą ØĻØąØĒŲØąØŊ ŲūØ§ØąØ§Ų
ØŠØąŲØ§Û ØŠŲØēÛØđ ØĒŲ
ÛØŪØŠŲ ÚŊاŲØģÛØ ØĻØąÚØģØĻâŲا Ûا Ų
ŲØŊØ§Øą Ų
ØŠØšÛØą ŲūŲŲاŲ ØąØ§ ŲÛØē Ų
ØīØŪØĩ Ų
ÛâÚĐŲØŊ.
ÚŊاŲ
اŲŲ (E-Step) ØĻØąØ§Û Ų
ØŊŲ ØŠØąÚĐÛØĻÛ ÚŊاŲØģÛ
ŲŲ
اŲØ·ŲØą ÚĐŲ ŲØĻŲا اØīØ§ØąŲ ØīØŊØ ØŠØ§ØĻØđ ØŠŲØēÛØđ ØĒŲ
ÛØŪØŠŲ ÚŊاŲØģÛ ØąØ§ Ų
ÛâØŠŲاŲ ØĻŲ ØĩŲØąØŠ ØŠØąÚĐÛØĻ ŲØēŲÛ Ø§Øē ÚŲØŊÛŲ ØŠŲØēÛØđ ŲØąŲ
اŲ ŲŲØīØŠ. ØĻŲاØĻØąØ§ÛŲ اÚŊØą ŲØēŲâŲا ØąØ§ ØĻا  ŲØīاŲ ØŊŲÛŲ
Ø ØĻØąØ§Û K ØŪŲØīŲ Ûا ØŠŲØēÛØđ ŲØąŲ
اŲØ ØŠØ§ØĻØđ ÚÚŊاŲÛ ØĒŲ
ÛØŪØŠŲ ØŊØą ŲŲØ·Ų x ØĻŲ ØĩŲØąØŠ ØēÛØą ŲŲØīØŠŲ ØŪŲاŲØŊ ØīØŊ.
ŲØīاŲ ØŊŲÛŲ
Ø ØĻØąØ§Û K ØŪŲØīŲ Ûا ØŠŲØēÛØđ ŲØąŲ
اŲØ ØŠØ§ØĻØđ ÚÚŊاŲÛ ØĒŲ
ÛØŪØŠŲ ØŊØą ŲŲØ·Ų x ØĻŲ ØĩŲØąØŠ ØēÛØą ŲŲØīØŠŲ ØŪŲاŲØŊ ØīØŊ.
 ØĻŲ ÚĐŲ
ÚĐ ŲاŲŲŲ ØĻÛØē ØŊØą اØØŠŲ
اŲ ØīØąØ·Û ØŠØ§ØĻØđ اØØŠŲ
اŲ ŲūØģÛŲ ØĻØąØ§Û Ų
ØŠØšÛØą ŲūŲŲاŲ Z ÚĐŲ ØĻŲ ØĩŲØąØŠ
ØĻŲ ÚĐŲ
ÚĐ ŲاŲŲŲ ØĻÛØē ØŊØą اØØŠŲ
اŲ ØīØąØ·Û ØŠØ§ØĻØđ اØØŠŲ
اŲ ŲūØģÛŲ ØĻØąØ§Û Ų
ØŠØšÛØą ŲūŲŲاŲ Z ÚĐŲ ØĻŲ ØĩŲØąØŠ  ŲØīاŲ ØŊاØŊŲ ØīØŊŲØ ØĻŲ ØĩŲØąØŠ ØēÛØą ØŊØą ØŪŲاŲØŊ ØĒŲ
ØŊ. اŲØĻØŠŲ ØŊØą ŲØļØą ØŊاØīØŠŲ ØĻاØīÛØŊ ÚĐŲ ؊اØĻØđ اØØŠŲ
اŲ ŲūÛØīÛŲ ØŊØą اÛŲ ØاŲØŠ ŲŲ
اŲ Ï Ø§ØģØŠ.
ŲØīاŲ ØŊاØŊŲ ØīØŊŲØ ØĻŲ ØĩŲØąØŠ ØēÛØą ØŊØą ØŪŲاŲØŊ ØĒŲ
ØŊ. اŲØĻØŠŲ ØŊØą ŲØļØą ØŊاØīØŠŲ ØĻاØīÛØŊ ÚĐŲ ؊اØĻØđ اØØŠŲ
اŲ ŲūÛØīÛŲ ØŊØą اÛŲ ØاŲØŠ ŲŲ
اŲ Ï Ø§ØģØŠ.

ÚŊاŲ
ØŊŲŲ
(M-Step) ØĻØąØ§Û Ų
ØŊŲ ØŠØąÚĐÛØĻÛ ÚŊاŲØģÛ
ŲūØģ اØē Ų
ØاØģØĻŲ ؊اØĻØđ اØØŠŲ
اŲ ŲūØģÛŲ ØĻØąØ§Û Ų
ØŠØšÛØą ŲūŲŲاŲØ ØĻاÛØŊ ŲūØ§ØąØ§Ų
ØŠØąŲØ§Û ØŠŲØēÛØđ ØĒŲ
ÛØŪØŠŲ ÚŊاŲØģÛ ØąØ§ ØĻØąØĒŲØąØŊ ÚĐØąØŊŲ ØģŲūØģ Ų
ŲØŊØ§Øą ŲÚŊØ§ØąÛØŠŲ
؊اØĻØđ ØŊØąØģØŠŲŲ
اÛÛ ØąØ§ Ų
ØاØģØĻŲ ÚĐŲÛŲ
. اÛŲ ÚŊاŲ
âŲا ؊ا ØąØģÛØŊŲ ØĻŲ ŲŲ
ÚŊØąØ§ÛÛ ØŊØą Ų
ŲØŊØ§Øą ؊اØĻØđ ØŊØąØģØŠŲŲ
اÛÛ ØŠÚĐØąØ§Øą ØŪŲاŲØŊ ØīØŊ.
Ų
ÛاŲÚŊÛŲ ØĻØąØ§Û ØŪŲØīŲâ kاŲ
ØĻŲ ØĩŲØąØŠ ØēÛØą ØĻØąØĒŲØąØŊ Ų
ÛâØīŲØŊ.

 ØĻØąØ§Û ØĻØąØĒŲØąØŊ ŲØēŲâ ØĻØąØ§Û ŲØą ÛÚĐ Ø§Øē ØŠŲØēÛØđâŲا ŲÛØē اØē ØąØ§ØĻØ·Ų ØēÛØą اØģØŠŲاØŊŲ Ų
ÛâÚĐŲÛŲ
.
ØĻØąØ§Û ØĻØąØĒŲØąØŊ ŲØēŲâ ØĻØąØ§Û ŲØą ÛÚĐ Ø§Øē ØŠŲØēÛØđâŲا ŲÛØē اØē ØąØ§ØĻØ·Ų ØēÛØą اØģØŠŲاØŊŲ Ų
ÛâÚĐŲÛŲ
.
 ØĻŲ اÛŲ ØŠØąØŠÛØĻ ؊اØĻØđ ÚĐŲ ØŊØą اØŊاŲ
Ų ŲاØĻŲ Ų
ØīاŲØŊŲ اØģØŠ ØĻاÛØŊ ØĻÛØīÛŲŲ ØīŲØŊ.
ØĻŲ اÛŲ ØŠØąØŠÛØĻ ؊اØĻØđ ÚĐŲ ØŊØą اØŊاŲ
Ų ŲاØĻŲ Ų
ØīاŲØŊŲ اØģØŠ ØĻاÛØŊ ØĻÛØīÛŲŲ ØīŲØŊ.
 ØاŲ ØĻا ØŠŲØŽŲ ØĻŲ اÛŲÚĐŲ ŲÚŊØ§ØąÛØŠŲ
ÛÚĐ ØŠØ§ØĻØđ Ų
ŲØđØą Ų
ØØģŲØĻ Ų
ÛâØīŲØŊ اØē ŲاŲ
ØģاŲÛ ØŽŲØģŲ اØģØŠŲاØŊŲ ÚĐØąØŊŲ Ų ØģØđÛ Ų
ÛâÚĐŲÛŲ
؊اØĻØđ ØēÛØą ÚĐŲ ÚĐØąØ§Ų ŲūاÛÛŲ ØĻØąØ§Û ØŠØ§ØĻØđ ØĻاŲا اØģØŠ ØąØ§ ØĻÛØīÛŲŲ ÚĐŲÛŲ
.
ØاŲ ØĻا ØŠŲØŽŲ ØĻŲ اÛŲÚĐŲ ŲÚŊØ§ØąÛØŠŲ
ÛÚĐ ØŠØ§ØĻØđ Ų
ŲØđØą Ų
ØØģŲØĻ Ų
ÛâØīŲØŊ اØē ŲاŲ
ØģاŲÛ ØŽŲØģŲ اØģØŠŲاØŊŲ ÚĐØąØŊŲ Ų ØģØđÛ Ų
ÛâÚĐŲÛŲ
؊اØĻØđ ØēÛØą ÚĐŲ ÚĐØąØ§Ų ŲūاÛÛŲ ØĻØąØ§Û ØŠØ§ØĻØđ ØĻاŲا اØģØŠ ØąØ§ ØĻÛØīÛŲŲ ÚĐŲÛŲ
.
![{\displaystyle L=\sum _{n=1}^{N}\sum _{k=1}^{K}\operatorname {E} [z_{nk}]{\Big \{}\ln \pi _{k}+\ln {N}(x_{n}|\mu _{k}\,\Sigma _{k}){\Big \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cbf445e77886b4fb1d30bcd5afa8460b69f54f9)
Ų
ŲاØĻØđ
- â "Mixture model". Wikipedia (ØĻŲ اŲÚŊŲÛØģÛ). 2023-06-18.
- â Guoshen Yu; Sapiro, G.; Mallat, S. (2012-05). "Solving Inverse Problems With Piecewise Linear Estimators: From Gaussian Mixture Models to Structured Sparsity". IEEE Transactions on Image Processing. 21 (5): 2481â2499. doi:10.1109/TIP.2011.2176743. ISSN 1057-7149.