ماشین تورینگ متناوب
|
Read other articles:

В Википедии есть статьи о других людях с фамилией Бессонов. Геннадий Бессонов Личная информация Пол мужской Полное имя Бессонов Геннадий Вениаминович Страна СССР → Россия Специализация тяжёлая атлетика Клуб «Спартак»«Динамо» (с 1978) Дата рождения 28 апреля 1954(1954-04-...

ولد عبد الرحمان كاكي معلومات شخصية اسم الولادة ولد عبد الرحمان عبد القادر الميلاد 18 فبراير 1934(1934-02-18)مستغانم الوفاة 14 فبراير 1995 (60 سنة)وهران مواطنة الجزائر الحياة العملية المهنة ممثل مسرحي اللغات العربية المواقع IMDB صفحته على IMDB تعديل مصدري - تعديل عبد الرحمان كا
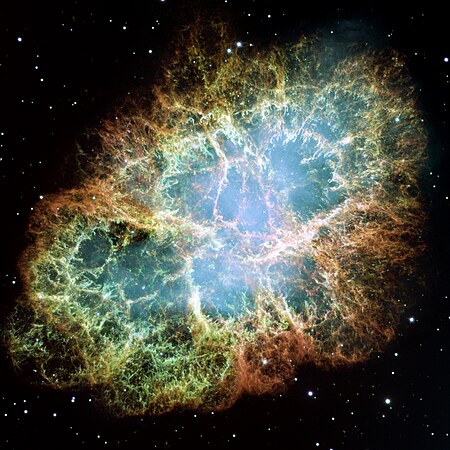
(7321) 1979 MZ2ВідкриттяВідкривач Е. Гелін,Ш. Дж. БасМісце відкриття Обсерваторія Сайдинг-СпрінгДата відкриття 25 червня 1979ПозначенняНазвана на честь Minerva Hamilton HoytdТимчасові позначення 1979 MZ2 1990 FU2Категорія малої планети Астероїд головного поясуОрбітальні характеристики[1] Еп

Latour-Bas-Elne Gemeente in Frankrijk Situering Regio Occitanie Departement Pyrénées-Orientales (66) Arrondissement Perpignan Kanton La Côte Radieuse Coördinaten 42° 37′ NB, 3° 0′ OL Algemeen Oppervlakte 3,31 km² Inwoners (1 januari 2020) 3.210[1] (970 inw./km²) Hoogte 4 - 29 m Burgemeester Pierre Roge (maart 2001) Overig Postcode 66200 INSEE-code 66094 Foto's Portaal Frankrijk Latour-Bas-Elne (Catalaans: La Torre d'Elna) is een gemeente in het Franse ...

1914 film The Wishing Ring: An Idyll of Old EnglandNewspaper advertisement.Directed byMaurice TourneurWritten byMaurice Tourneur (scenario)Based onThe Wishing Ringby Owen DavisProduced byWilliam A. BradyShubert familyStarringVivian MartinCinematographyJohn van den BroekDistributed byWorld Film CompanyRelease date November 9, 1914 (1914-11-09) Running time54 minutesCountryUnited StatesLanguagesSilentEnglish intertitles The Wishing Ring: An Idyll of Old England is a 1914 American...

Psorothamnus fremontii P. fremontii in St. George, Utah, (EE.UU.)TaxonomíaReino: PlantaeDivisión: MagnoliophytaClase: MagnoliopsidaOrden: FabalesFamilia: FabaceaeSubfamilia: FaboideaeTribu: AmorpheaeGénero: PsorothamnusEspecie: P. fremontii(Torr. ex A.Gray) Barneby[editar datos en Wikidata] Psorothamnus fremontii es un arbusto de la familia de las fabáceas.[1] Descripción Debe su nombre específico al explorador John C. Frémont, cuyo nombre está relacinonado a v...

Місто Токкополаангл. Toccopola Координати 34°15′20″ пн. ш. 89°14′03″ зх. д. / 34.25580000002777581° пн. ш. 89.234400000027775945° зх. д. / 34.25580000002777581; -89.234400000027775945Координати: 34°15′20″ пн. ш. 89°14′03″ зх. д. / 34.25580000002777581° пн. ш. 89.234400000027775945° зх. д.&#...

Cet article est une ébauche concernant Nancy et son agglomération. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Analyse et traitement informatique de la langue françaiseHistoireFondation 2001CadreSigle (mul) ATILFCode UMR7118Type Unité mixte de recherchePays FranceCoordonnées 48° 41′ 35″ N, 6° 09′ 58″ EOrganisationOrganisations mères Université Nancy-II...

1956 AFC Asian CupAsian Cup Hong Kong 19561956年亞洲盃足球賽Tournament detailsHost countryHong KongDates1–15 SeptemberTeams4Venue(s)1 (in 1 host city)Final positionsChampions South Korea (1st title)Runners-up IsraelThird place Hong KongFourth place South VietnamTournament statisticsMatches played6Goals scored27 (4.5 per match)Attendance136,000 (22,667 per match)Top scorer(s) Nahum Stelmach(4 goals)1960 → International football competition...

Вевр-е-МонтуальVaivre-et-Montoille Країна Франція Регіон Бургундія-Франш-Конте Департамент Верхня Сона Округ Везуль Кантон Везуль-Уест Код INSEE 70513 Поштові індекси 70000 Координати 47°37′53″ пн. ш. 6°06′18″ сх. д.H G O Висота 212 - 380 м.н.р.м. Площа 8,48 км² Населення 2420 (01-2...

جزء من سلسلة مقالات سياسة الجزائر الدستور الدستور حقوق الإنسان السلطة التنفيذية الرئيس (قائمة) عبد المجيد تبون رئيس الحكومة (قائمة) عبد العزيز جراد السلطة التشريعية البرلمان مجلس الأمّة المجلس الشعبي الوطني السلطة القضائية السلطة القضائية المحكمة العليا التقسيمات الإدا�...

State park in South Dakota, United States Custer State ParkAmerican bison at the Wildlife Loop RoadLocation of Custer State Park in South DakotaLocationCuster County, South Dakota, United StatesCoordinates43°44′45″N 103°25′5″W / 43.74583°N 103.41806°W / 43.74583; -103.41806Area71,000 acres (290 km2)Elevation4,721 ft (1,439 m)[1]Established1912Named forGeorge Armstrong CusterGoverning bodySouth Dakota Department of Game, Fish &...

Barry Fitzgerald foi nomeado nas categorias Melhor Actor e Melhor Actor Secundário pelo seu desempenho no filme Going My Way, tendo vencido a última categoria. A seguir apresenta-se a lista dos atores que receberam nomeações para dois prémios da Academia no mesmo ano. A Academy of Motion Picture Arts and Sciences (em português: Academia de Artes e Ciências Cinematográficas) teve ocorrências de actores e actrizes nomeados para dois prémios da Academia em categorias de actuação em u...

British political commentator and activist Darren GrimesGrimes in 2021Born (1993-07-22) 22 July 1993 (age 30)Consett, County Durham, EnglandNationalityBritishEducationTanfield SchoolOccupation(s)Digital manager, political activist Darren Grimes (born 22 July 1993[1]) is a British right-wing[2] political commentator and activist. A Liberal Democrat activist before dropping out of university, he then worked for a number of Brexit campaigns. He set up the website Reasoned in...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (أبريل 2011) التكاليف وأجرة الشحن (بالإنجليزية: Cost and Freight : C.& F) أو البيع مع الالتزام بنفقات البضاعة وأجرة النقل ي�...

Hindu Temple Kumara Swamy DevasthanaReligionAffiliationHinduismDistrictBangaloreDeityLord Kumara SwamyLocationLocationBangaloreStateKarnatakaCountryIndia Kumara Swamy Devasthana (Kannada: ಶ್ರೀ ಕುಮಾರಸ್ವಾಮಿ ದೇವಸ್ಥಾನ, romanized: Śrī kumārasvāmi dēvasthāna), also known as Sri Kumaraswaami Temple, is a Hindu temple located in Hanumanthanagar, in the city of Bangalore, Karnataka, southern India.[1][2] It is dedicated to the go...

Species of flowering plant Eriodictyon altissimum Conservation status Endangered (ESA) Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Asterids Order: Boraginales Family: Boraginaceae Genus: Eriodictyon Species: E. altissimum Binomial name Eriodictyon altissimumP.V.Wells Eriodictyon altissimum is a rare species of flowering plant in the borage family known by the common name Indian Knob mountainbalm. It is endemic to San Luis...

Australian rugby competition 2013 New South Wales CupLeagueNew South Wales CupTeams13Champions Cronulla-Sutherland SharksRunners-up Windsor WolvesPremiership winners Cronulla-Sutherland SharksWooden spoon Wyong RoosMan of SteelMitch Williams ( Wyong Roos)Ron Massey CupNumber of teams12Premiers Wentworthville MagpiesMinor Premiers Cabramatta Two BluesRunners-up MountiesPlayer of the yearDean Rysko ( Western Suburbs Magpies)Sydney ShieldPremiers Belrose EaglesMinor Premiers Belrose EaglesRunner...

3rd United States intra-term presidential inauguration Presidential inauguration ofAndrew JohnsonSwearing-in ceremony in the Kirkwood House (Frank Leslie's Illustrated Newspaper, January 6, 1866)DateApril 15, 1865; 158 years ago (1865-04-15)LocationKirkwood House,Washington, D.C.ParticipantsAndrew Johnson17th president of the United States— Assuming officeSalmon P. ChaseChief Justice of the United States— Administering oath← 18651869 → This article ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Makhdoom Mohiuddin – news · newspapers · books · scholar · JSTOR (April 2022) (Learn how and when to remove this template message) Makhdoom MohiuddinBorn(1908-02-04)4 February 1908Andole, Medak District, Hyderabad State, British Indian Empire(now in Telangana, ...





































