![]() Ï¿Ï▒┘üϻϺ┘å┘ç ┌®┘ÅÏ« Ï│Ϻϻ┘çÔÇîϬÏ▒█î┘å ┘å┘êÏ╣ ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ϺÏ│Ϭ.
Ï¿Ï▒┘üϻϺ┘å┘ç ┌®┘ÅÏ« Ï│Ϻϻ┘çÔÇîϬÏ▒█î┘å ┘å┘êÏ╣ ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ϺÏ│Ϭ.
 ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ┘à┘åÏ»┘äÏ¿Ï▒┘ê █î┌® ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä Ï│┘çÔÇîÏ¿Ï╣Ï»█î ϺÏ▓ ┘àϼ┘à┘êÏ╣┘ç ┘à┘åÏ»┘äÏ¿Ï▒┘ê ┘à█îÔÇîϿϺÏ┤Ï» ┌®┘ç Ï¿┘çÔÇî┘êÏ│█î┘ä┘ç ϻϺ┘å█î┘ä ┘êϺ█îϬ ┘ê ┘¥Ïº┘ê┘ä ┘åϺ█î┘äϺ┘åÏ»Ï▒ Ï│ϺϫϬ┘ç Ï┤Ï»┘çÔÇîϺÏ│Ϭ.
┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ┘à┘åÏ»┘äÏ¿Ï▒┘ê █î┌® ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä Ï│┘çÔÇîÏ¿Ï╣Ï»█î ϺÏ▓ ┘àϼ┘à┘êÏ╣┘ç ┘à┘åÏ»┘äÏ¿Ï▒┘ê ┘à█îÔÇîϿϺÏ┤Ï» ┌®┘ç Ï¿┘çÔÇî┘êÏ│█î┘ä┘ç ϻϺ┘å█î┘ä ┘êϺ█îϬ ┘ê ┘¥Ïº┘ê┘ä ┘åϺ█î┘äϺ┘åÏ»Ï▒ Ï│ϺϫϬ┘ç Ï┤Ï»┘çÔÇîϺÏ│Ϭ.


 ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î ϺÏ▓ ┘àϼ┘à┘êÏ╣┘ç ┘à┘åÏ»┘äÏ¿Ï▒┘ê
┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î ϺÏ▓ ┘àϼ┘à┘êÏ╣┘ç ┘à┘åÏ»┘äÏ¿Ï▒┘ê
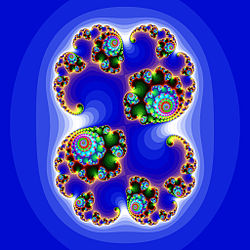 ┘àϼ┘à┘êÏ╣┘ç ┌ÿ┘ê┘ä█îϺ
┘àϼ┘à┘êÏ╣┘ç ┌ÿ┘ê┘ä█îϺ
 ┌®┘ä┘à Ï▒┘ê┘à█î
┌®┘ä┘à Ï▒┘ê┘à█î
┘üÏ▒Ϻ┌®Ï¬Ïº┘ä █îϺ Ï¿┘ÄÏ▒ϫϺ┘ä[█▒] (Ï¿┘ç Ϻ┘å┌»┘ä█îÏ│█î: Fractal)Ïî Ï│ϺϫϬϺÏ▒█î ┘ç┘åÏ»Ï│█î ϺÏ│Ϭ ┌®┘ç ϿϺ Ï¿Ï▓Ï▒┌» ┌®Ï▒Ï»┘å ┘çÏ▒ Ï¿Ï«Ï┤ ϺÏ▓ Ϻ█î┘å Ï│ϺϫϬϺÏ▒ Ï¿┘ç ┘åÏ│ϿϬ ┘àÏ╣█î┘åÏî ┘ç┘àϺ┘å Ï│ϺϫϬϺÏ▒ ┘åÏ«Ï│Ϭ█î┘å Ï¿┘ç Ï»Ï│Ϭ Ïó█îÏ». Ï¿┘ç ┌»┘üϬϺÏ▒█î Ï»█î┌»Ï▒ ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä Ï│ϺϫϬϺÏ▒█î ϺÏ│Ϭ ┌®┘ç ┘çÏ▒ Ï¿Ï«Ï┤ ϺÏ▓ Ïó┘å ϿϺ ┌®┘äÔÇîϺÏ┤ ┘ç┘àϺ┘å┘åÏ» ϺÏ│Ϭ. ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ϺÏ▓ Ï»┘êÏ▒ ┘ê ┘åÏ▓Ï»█î┌® █î┌®Ï│Ϻ┘å Ï»█îÏ»┘ç ┘à█îÔÇîÏ┤┘êÏ». Ï¿┘ç Ϻ█î┘å ┘ê█î┌ÿ┌»█î Ï«┘êÏ»┘ç┘àϺ┘å┘åÏ»█î ┌»┘ê█î┘åÏ».[█▓] ┘üÏ▒Ϻ┌®Ï¬Ïº┘äÔÇî┘çϺ █î┌®█î ϺÏ▓ ϺϿÏ▓ϺÏ▒┘çϺ█î ┘à┘ç┘à Ï»Ï▒ ┌»Ï▒Ϻ┘ü█î┌® Ï▒Ϻ█îϺ┘å┘çÔÇîϺ█î ┘çÏ│Ϭ┘åÏ» ┘ê ┘à█îÔÇîϬ┘êϺ┘å ϺÏ│Ϭ┘üϺϻ┘çÔÇî┘çϺ█î Ï¿Ï│█îϺÏ▒█î ϺÏ▓ Ïó┘åÔÇî┘çϺ ┌®Ï▒Ï»
┘åϺ┘àÔÇî┌»Ï░ϺÏ▒█î
┘üÏ▒┌®Ï¬Ïº┘ä fractal ϺÏ▓ ┘êϺ┌ÿ┘ç ┘äϺϬ█î┘å fractus █îϺ fractum Ï¿┘ç ┘àÏ╣┘å█î Ï┤┌®Ï│Ϭ┘ç ┌»Ï▒┘üϬ Ï┤Ï»┘çÔÇîϺÏ│Ϭ ┌®┘ç Ï¿█îϺ┘å┌»Ï▒ █î┌®█î ϺÏ▓ Ï┤┘åϺÏ│┘çÔÇî┘çϺ█î ϺÏÁ┘ä█î Ïó┘å █îÏ╣┘å█î -Ï¿Ï«Ï┤ÔÇîÏ┤Ï»┘å█î- ϺÏ│Ϭ.
┘üÏ▒┘ç┘å┌»Ï│ϬϺ┘å Ï▓ϿϺ┘å ┘üϺÏ▒Ï│█î ┘êϺ┌ÿ┘ç Ï¿Ï▒ϫϺ┘ä Ï▒Ϻ ϬÏÁ┘ê█îÏ¿ ┌®Ï▒Ï»┘ç ┘ê ┘ç┘à┌å┘å█î┘å Ï¿Ï▒Ϻ█î ┘êϺ┌ÿ┘ç ┘üÏ▒┌®Ï¬Ïº┘ä█î ┘êϺ┌ÿ┘ç Ï¿Ï▒ϫϺ┘ä█î Ï▒Ϻ ϬÏÁ┘ê█îÏ¿ ┌®Ï▒Ï»┘çÔÇîϺÏ│Ϭ ┌®┘ç ϺÏ▓ ┘êϺ┌ÿ┘ç Ï¿Ï▒Ï« Ï¿┘ç ┘àÏ╣┘å█î Ï¿Ï«Ï┤ ┘ê ┘éÏ│┘àϬ ┘ê ┘¥Ï│┘ê┘åÏ» -Ϻ┘ä (┘àϺ┘å┘åÏ» ┌å┘å┌»Ïº┘ä) ϬÏ┤┌®█î┘ä Ï┤Ï»┘çÔÇîϺÏ│Ϭ ┘ê ϿϺ ┘êϺ┌ÿ┘ç ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ┘ç┘àÔÇî┘àÏ╣┘å█î ϺÏ│Ϭ.[█▓]
┌®Ï┤┘ü
┘êϺ┌ÿ┘ç ┘üÏ▒┌®Ï¬Ïº┘ä Ï»Ï▒ Ï│Ϻ┘ä █▒█╣█À█ Ϭ┘êÏ│ÏÀ Ï▒█îϺÏÂ█îϻϺ┘å ┘üÏ▒Ϻ┘åÏ│┘ê█î Ï¿┘å┘êÏó ┘à┘åÏ»┘äÏ¿Ï▒┘ê ┘êϺÏ▒Ï» Ï»┘å█îϺ█î Ï▒█îϺÏÂ█î Ï┤Ï». ┘àϺ┘åÏ»┘äÏ¿Ï▒┘ê ┘ç┘å┌»Ïº┘à█î ┌®┘ç ┘¥█îÏ▒Ϻ┘à┘ê┘å ÏÀ┘ê┘ä Ï│┘êϺϡ┘ä Ϻ┘å┌»┘ä█îÏ│ ┘¥┌ÿ┘ê┘çÏ┤ ┘à█îÔÇî┌®Ï▒Ï»Ïî Ï»Ï▒█îϺ┘üϬ ┌®┘ç ┘çÏ▒┌»Ïº┘ç ϿϺ ┘à┘é█îϺÏ│ Ï¿Ï▓Ï▒┌» Ϻ█î┘å ÏÀ┘ê┘ä Ϻ┘åϻϺÏ▓┘ç ┌»Ï▒┘üϬ┘ç Ï┤┘êÏ» Ï¿█îÏ┤ϬÏ▒ ϺÏ▓ Ï▓┘àϺ┘å█î ϺÏ│Ϭ ┌®┘ç ┘à┘é█îϺÏ│ ┌®┘ê┌å┌®ÔÇîϬÏ▒ ϿϺÏ┤Ï».
┘ê█î┌ÿ┌»█î Ï┤┌®┘ä ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î
- ϿϺ Ϭ┘êϼ┘ç Ï¿┘ç ┘åÏ¡┘ê┘ç Ï┤┌®┘äÔÇî┌»█îÏ▒█î Ïó┘å ┘éϺϿ┘ä ┘¥█îÏ┤ÔÇîÏ¿█î┘å█î ϺÏ│Ϭ.
- ┘üÏ▒┌»Ï┤Ϭ (Ϭ┌®Ïº┘à┘ä) ┘ç┘àÔÇîÏ▓┘àϺ┘å ϻϺÏ▒Ï».
- ϻϺÏ▒Ϻ█î ϼϺ█î┌»Ï▓█î┘å█î Ï¿┘ç█î┘å┘ç ϺÏ│Ϭ.
- Ï▒█îÏ┤┘ç Ï»Ï▒ ┘é┘êϺ┘å█î┘å Ï│Ϻϻ┘ç ϻϺÏ▒Ï».
- Ï»Ï▒ Ï┤┌®┘äÔÇî┌»█îÏ▒█î ┌»┘ê┘å┘ç ϺÏ▓ Ϭ┌®Ï▒ϺÏ▒ Ï¿┘çÏ▒┘çÔÇî┘à█îÔÇîϼ┘ê█îÏ».
- Ï│Ϻ┘àϺ┘å┘çÔÇîϺ█î Ϭ┘ê Ï»Ï▒ Ϭ┘ê ϺÏ│Ϭ.
- Ï▒█îϫϬÔÇî┘çϺ█î Ϻ┘é┘ä█îÏ»Ï│█î ϿϺ ϺÏ│Ϭ┘üϺϻ┘ç ϺÏ▓ Ϭ┘êϺϿÏ╣ Ϻ█îÏ│ϬϺ Ï│ϺϫϬ┘ç ┘à█îÔÇîÏ┤┘ê┘åÏ» ┘ê┘ä█î Ï▒█îϫϬÔÇî┘çϺ█î ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ϿϺ ┘üÏ▒Ϻ█î┘åÏ»┘çϺ█î ┘¥┘ê█îϺ Ï│ϺϫϬ┘ç ┘à█îÔÇîÏ┤┘ê┘åÏ». ┘üÏ▒Ϻ█î┘åÏ»┘çϺ█î ┘¥┘ê█îϺÏî ┘üÏ▒Ϻ█î┘åÏ»┘çϺ█î█î ┘çÏ│Ϭ┘åÏ» ┌®┘ç ϻϺÏ▒Ϻ█î ϡϺ┘üÏ©┘ç ┘à█îÔÇîϿϺÏ┤┘åÏ» ┘ê Ï▒┘üϬϺÏ▒ Ïó┘åÔÇî┘çϺ Ï¿┘ç ┌»Ï░Ï┤Ϭ┘ç Ï¿Ï│Ϭ┌»█î ϻϺÏ▒Ï».
- ϻϺÏ▒Ϻ█î ┘ê█î┌ÿ┌»█î Ï«┘êÏ» ┘ç┘àϺ┘å┘åÏ»█î ϺÏ│Ϭ.
- ┘çÏ▒ ┘üÏ▒Ϻ█î┘åÏ» Ϭ┌®Ï▒ϺÏ▒█î ┘ê ┘¥┘ê█îϺ ϿϺÏ╣Ͻ Ϻ█îϼϺϻ Ï│ϺϫϬϺÏ▒┘çϺ█î ┘¥█î┌å█îÏ»┘ç ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ┘å┘à█îÔÇîÏ┤┘êÏ». Ï│ϺÏ▓┘ê┌®ÏºÏ▒ ┘üÏ▒Ïó┘êÏ▒█î ┌å┘å█î┘å Ï│ϺϫϬϺÏ▒┘çϺ█î ┘¥┘ê█îϺ█î█îÏî ÏóÏ┤┘êÏ¿ ϺÏ│Ϭ. Ï»Ï▒ Ï¡┘é█î┘éϬÏî ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ┘å┌»ÏºÏ▒┘çÔÇîϺ█î Ï▒█îϺÏÂ█î ϺÏ▓ ÏóÏ┤┘êÏ¿ ϺÏ│Ϭ.
┘ç┘åÏ»Ï│┘ç ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î
┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ϺÏ▓ Ï»█îÏ» ┘ç┘åÏ»Ï│█î Ï¿┘ç ┌å█îÏ▓┘çϺ█î█î ┘à█îÔÇî┌»┘ê█î┘åÏ» ┌®┘ç ϻϺÏ▒Ϻ█î Ϻ█î┘å Ï│┘ç ┘ê█î┌ÿ┌»█î ϿϺÏ┤Ï»:
- ϻϺÏ▒Ϻ█î ┘ê█î┌ÿ┌»█î Ï«┘êÏ»┘ç┘àϺ┘å┘åÏ»█î ϿϺÏ┤Ï» █îϺ Ï¿┘ç Ϻ┘å┌»┘ä█îÏ│█î self-similar ϿϺÏ┤Ï».
- Ï»Ï▒ ┘à┘é█îϺÏ│ Ï«Ï▒Ï» Ï¿Ï│█îϺÏ▒ ┘¥█î┌å█îÏ»┘ç ϿϺÏ┤Ï».
- Ï¿Ï╣Ï» Ïó┘å █î┌® Ï╣ϻϻ ÏÁÏ¡█îÏ¡ (┘àϽ┘äϺ┘ï █▓) ┘åϿϺÏ┤Ï».
┘àϡϺÏ│Ï¿┘ç Ï¿┘ÅÏ╣Ï» ┘üÏ▒Ϻ┌®Ï¬Ïº┘äÔÇî┘çϺ
Ï¿Ï╣Ï» Ï«ÏÀ █î┌®Ïî Ï¿Ï╣Ï» ÏÁ┘üÏ¡┘ç Ï»┘ê ┘ê Ï¿Ï╣Ï» ┘üÏÂϺ Ï│┘ç ϺÏ│Ϭ. ┘üÏ▒Ϻ┌®Ï¬Ïº┘äÔÇî┘çϺ Ï¿Ï▒Ï«┘äϺ┘ü ┘ç┘à┘ç┘ö Ϻ█î┘åÔÇî┘çϺ Ï¿Ï╣Ï» ÏÁÏ¡█îÏ¡ ┘åϻϺÏ▒┘åÏ». Ï¿Ï▒Ϻ█î ┘å┘à┘ê┘å┘ç Ï¿Ï╣Ï» █î┌® ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ┘à█îÔÇîϬ┘êϺ┘åÏ» █▒┘½█▓ ϿϺÏ┤Ï» ┌®┘ç Ï¿Ï»█î┘å ┌å┘à ϺÏ▓ Ï«ÏÀ ┘¥█î┌å█îÏ»┘çÔÇîϬÏ▒ ┘ê ϺÏ▓ ÏÁ┘üÏ¡┘ç Ï│ϺϻϬÏ▒ ϺÏ│Ϭ. Ï¿Ï╣Ï» ┘üÏ▒Ϻ┌®Ï¬Ïº┘äÔÇî┘çϺ ϺÏ▓ █î┌® Ï│Ï▒█î ┘üÏ▒┘à┘ê┘äÔÇî┘çϺ█î ┘ä┌»ÏºÏ▒█îϬ┘à█î Ï¿Ï»Ï│Ϭ ┘à█îÔÇîÏó█î┘åÏ».
Ï┤┌®┘ä ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä
 ┘¥┘ê█îϺ┘å┘àϺ█î█î ϺÏ▓ Ï│ϺϫϬ┘ç Ï┤Ï»┘å █î┌® ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä Ï│Ϻϻ┘ç
┘¥┘ê█îϺ┘å┘àϺ█î█î ϺÏ▓ Ï│ϺϫϬ┘ç Ï┤Ï»┘å █î┌® ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä Ï│Ϻϻ┘ç
- Ï│Ϻ┘àϺ┘å┘ç Ï│ϺϫϬϺÏ▒█î Ϭ┌®Ï▒ϺÏ▒
Ϻ█î┘å Ï│█îÏ│Ϭ┘à ┌®┘ç ϻϺÏ▒Ϻ█î Ï╣┘äϺ┘àϬ ϺϫϬÏÁϺÏ▒█î IFS - Iterated Function System - ϺÏ│ϬÏî Ï│█îÏ│Ϭ┘à Ϭ┌®Ï▒ϺÏ▒ Ï▒Ϻ ┘àÏÀÏ▒Ï¡ ┘à█îÔÇî┌®┘åÏ» ┌®┘ç Ï¿┘ç ┘å┘êÏ╣█î ┘¥Ïº█î┘ç┘ö ┘ç┘åÏ»Ï│┘ç ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î ϺÏ│Ϭ.
Ϭ┌®Ï▒ϺÏ▒ █î┌®█î ϺÏ▓ Ï▒Ϻ┘çÔÇî┘çϺ█î Ϻ█îϼϺϻ ┘üÏ▒┘à Ï»Ï▒ ┘àÏ╣┘àϺÏ▒█î ϺÏ│Ϭ Ϻ┘àϺ Ï»Ï▒ ┘üÏ▒┌®Ï¬Ïº┘ä Ϻ█î┘å ┘üÏ▒┘à ϿϺ█îÏ│Ϭ█î ϻϺÏ▒Ϻ█î ┘àÏ┤Ï«ÏÁϺϬ ┘ç┘åÏ»Ï│█î ┌®┘ç Ï»Ï▒ ┘éÏ│┘àϬ ┘ç┘åÏ»Ï│┘ç ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î ┘àÏÀÏ▒Ï¡ Ï┤Ï» Ï▒Ϻ ϻϺÏ▒Ϻ ϿϺÏ┤Ï».
Ï¿┘çÔÇîÏÀ┘êÏ▒ ┌®┘ä█î Ϻ█î┘å Ϭ┌®Ï▒ϺÏ▒ ┘à█îÔÇîϬ┘êϺ┘åÏ» ϺÏ▓ ┌®┘åϺÏ▒ ┘ç┘à ┘éÏ▒ϺÏ▒ ┌»Ï▒┘üϬ┘å █î┌® Ï┤█îÏí Ï¿Ï»Ï│Ϭ Ïó█îÏ» █îϺ Ϻ█î┘å┌®┘ç █î┌® ┘à┘êÏÂ┘êÏ╣ ┘åÏ│ϿϬ Ï¿┘ç ┘à┘êÏÂ┘êÏ╣ Ï»█î┌»Ï▒ ┘ê Ï¿┘çÔÇîÏÀ┘êÏ▒ ┘àϬ┘êϺ┘ä█î ┌®┘ê┌å┌® Ï┤┘êÏ».
- Ï«┘êÏ»┘ç┘àϺ┘å┘åÏ»█î
Ï┤█îϪ█î Ï▒Ϻ ϻϺÏ▒Ϻ█î ϫϺÏÁ█îϬ Ï«┘êÏ» ┘àϬÏ┤ϺϿ┘ç█î ┘à█îÔÇî┌»┘ê█î█î┘à ┌®┘ç ┘çÏ▒ ┌»Ïº┘ç ┘éÏ│┘àϬÔÇî┘çϺ█î█î ϺÏ▓ Ïó┘å ϿϺ █î┌® ┘à┘é█îϺÏ│ ┘àÏ╣┘ä┘ê┘àÏî █î┌® ┘å┘à┘ê┘å┘ç ϺÏ▓ ┌®┘ä Ï┤█îϪ█î ϿϺÏ┤Ï». Ï│Ϻϻ┘çÔÇîϬÏ▒█î┘å ┘àϽϺ┘ä Ï¿Ï▒Ϻ█î █î┌® Ï┤█îϪ Ï«┘êÏ» ┘àϬÏ┤ϺϿ┘ç Ï»Ï▒ ÏÀÏ¿█îÏ╣Ϭ ┌»┘ä ┌®┘ä┘à ϺÏ│Ϭ ┌®┘ç ┘çÏ▒ ┘éÏÀÏ╣┘ç┘ö ┌®┘ê┌å┌® ┌»┘ä ┌®┘ä┘à ┘àϬÏ┤ϺϿ┘ç ┘éÏÀÏ╣┘ç Ï¿Ï▓Ï▒┌»█î ϺÏ▓ Ïó┘å ϺÏ│Ϭ.
┘ç┘à█î┘åÔÇîÏÀ┘êÏ▒ Ï»Ï▒ϫϬ ┌®ÏºÏ¼ █î┌® Ï┤█îϪ Ï«┘êÏ» ┘àϬÏ┤ϺϿ┘ç ϺÏ│ϬÏî ┌åÏ▒Ϻ ┌®┘ç ┘çÏ▒ █î┌® ϺÏ▓ Ï┤Ϻϫ┘çÔÇî┘çϺ█î Ïó┘å Ï«█î┘ä█î Ï┤Ï¿█î┘ç █î┌® Ï»Ï▒ϫϬ ┌®ÏºÏ¼ ϺÏ│Ϭ ┘ê┘ä█î Ï»Ï▒ ┘à┘é█îϺÏ│ Ï¿Ï│█îϺÏ▒ ┌®┘ê┌å┌®Ï¬Ï▒. ┘ç┘à┌å┘å█î┘å Ï»Ï▒ ┘à┘êÏ▒Ï» Ï¿Ï▒┌» Ï│Ï▒Ï«Ï│ ┘å█îÏ▓ ┌å┘å█î┘å ϫϺÏÁ█îϬ█î ┘êϼ┘êÏ» ϻϺÏ▒Ï».
Ï▒Ï┤Ϭ┘ç ┌®┘ê┘çÔÇî┘çϺÏî ┘¥Ï┤Ϭ┘çÔÇî┘çϺ█î ϺϿÏ▒Ïî ┘àÏ│█îÏ▒ Ï▒┘êϻϫϺ┘å┘çÔÇî┘çϺ ┘ê Ï«ÏÀ┘êÏÀ Ï│Ϻϡ┘ä█î ┘å█îÏ▓ ┘ç┘à┌»█î ┘àϽϺ┘äÔÇî┘çϺ█î█î ϺÏ▓ █î┌® Ï│ϺϫϬ┘àϺ┘å Ï«┘êÏ» ┘àϬÏ┤ϺϿ┘ç ┘çÏ│Ϭ┘åÏ».
┘üÏ▒Ϻ┌®Ï¬Ïº┘ä Ï┤┌®┘ä ┘ç┘åÏ»Ï│█î ┘¥█î┌å█îÏ»┘çÔÇîϺÏ│Ϭ ┌®┘ç ϻϺÏ▒Ϻ█î ϼÏ▓Ϫ█îϺϬ ┘àÏ┤ϺϿ┘ç Ï»Ï▒ Ï│ϺϫϬϺÏ▒ Ï«┘êÏ» Ï»Ï▒ ┘à┘é█îϺÏ│ÔÇî┘çϺ█î ┘àϬ┘üϺ┘êϬ ┘à█îÔÇîϿϺÏ┤Ï» ┘ê Ï¿█î ┘åÏ©┘à█î Ï»Ï▒ Ïó┘å ϺÏ▓ Ï»┘êÏ▒ ┘ê ┘åÏ▓Ï»█î┌® Ï¿┘ç █î┌® Ϻ┘åϻϺÏ▓┘ç ϺÏ│Ϭ.
ϼÏ│┘à ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î ϺÏ▓ Ï»┘êÏ▒ ┘ê ┘åÏ▓Ï»█î┌® █î┌®Ï│Ϻ┘å Ï»█îÏ»┘ç ┘à█îÔÇîÏ┤┘êÏ»Ïø ┘àϽ┘äϺ┘ï ┘ê┘éϬ█î Ï¿┘ç █î┌® ┌®┘ê┘ç ┘å┌»Ïº┘ç ┘à█îÔÇî┌®┘å█î┘à Ï┤┌®┘ä█î Ï┤Ï¿█î┘ç Ï¿┘ç █î┌® ┘àÏ«Ï▒┘êÏÀ ┘à█îÔÇîÏ¿█î┘å█î┘à ┌®┘ç Ï▒┘ê█î Ïó┘å ┘àÏ«Ï▒┘êÏÀ┘çϺ█î ┌®┘ê┌å┌®Ï¬Ï▒ ┘ê Ï¿█î ┘åÏ©┘à█î Ï»█îÏ»┘ç ┘à█îÔÇîÏ┤┘êÏ» ┘ê┘ä█î ┘ê┘éϬ█î ┘åÏ▓Ï»█î┌® ┘à█îÔÇîÏ┤┘ê█î┘à ┘ç┘à█î┘å ┘àÏ«Ï▒┘êÏÀÔÇî┘çϺ█î ┌®┘ê┌å┌® Ï┤Ï¿█î┘ç ┌®┘ê┘ç ┘çÏ│Ϭ┘åÏ» █îϺ Ï┤Ϻϫ┘çÔÇî┘çϺ█î █î┌® Ï»Ï▒ϫϬ Ï┤Ï¿█î┘ç Ï«┘êÏ» Ï»Ï▒ϫϬ ┘çÏ│Ϭ┘åÏ». Ϻ┘äϿϬ┘ç Ï»Ï▒ ÏÀÏ¿█îÏ╣Ϭ ┘å┘à┘ê┘å┘çÔÇî┘çϺ█î ϺϼÏ│Ϻ┘à ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ┘üÏ▒Ϻ┘êϺ┘å ϺÏ│Ϭ ┘àϽ┘äϺ┘ï ϺϿÏ▒┘çϺ -Ï▒┘êÏ»┘çϺ -Ï│Ï▒Ï«Ï│ÔÇî┘çϺ ┘ê ϡϬ█î ┌»┘ä ┌®┘ä┘à ϺÏ▓ ϺϼÏ│Ϻ┘à ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ϺÏ│ϬÏø ┘ê Ϻ┌»Ï▒ Ï¿┘ç Ï│ϺϫϬ┘çÔÇî┘çϺ█î Ï»Ï│Ϭ Ï¿Ï┤Ï▒ ┘ç┘à ┘å┌»Ïº┘ç ┌®┘å█î┘à ϬÏ▒ϺÏ┤┘çÔÇî┘çϺ█î Ï│█î┘ä█î┌®Ïº┘å █îϺ ┘àϽ┘äϽ Ï│Ï▒┘¥█î┘åÏ│┌®█î ┘å█îÏ▓ ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ┘çÏ│Ϭ┘åÏ»Ïø ┘ê Ï»Ï▒ ┘àÏ╣┘àϺÏ▒█î ┘ç┘à█îÏ┤┘ç ┘åϿϺ█îÏ» ┘å█îϺÏ▓ Ï¿Ï┤Ï▒ Ï▒Ϻ ┘ç┘åÏ»Ï│┘ç Ϻ┘é┘ä█îÏ»Ï│█î ϬÏú┘à█î┘å ┌®┘åÏ». ┌»Ï│ϬÏ▒Ï┤ Ï┤┘çÏ▒┘çϺ ┘å┘à┘ê┘å┘ç ÏóÏ┤┌®ÏºÏ▒█î ϺÏ▓ ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ϺÏ│Ϭ.
- ┘üÏ▒Ϻ┌®Ï¬Ïº┘äÔÇî┘çϺ█î ÏÀÏ¿█îÏ╣█î
Ϻ█î┘å ┘üÏ▒┘àÔÇî┘çϺ ┌®┘ç Ï¿┘ç ÏÁ┘êÏ▒Ϭ ÏÀÏ¿█îÏ╣█î ┘êϼ┘êÏ» ϻϺÏ▒┘åÏ» ϻϺÏ▒Ϻ█î Ï│ϺϫϬϺÏ▒█î Ï«┘êÏ» ┘àϬÏ┤ϺϿ┘ç ┘çÏ│Ϭ┘åÏ» ϡϬ█î Ï»Ï▒ ┘à┘é█îϺÏ│ ┘à█î┌®Ï▒┘êÏ│┌®┘¥█î █î┌®ÔÇîϻϺ┘å┘ç Ï¿Ï▒┘ü ϻϺÏ▒Ϻ█î ┘üÏ▒┘à█î Ï«┘êÏ» ┘àϬÏ┤ϺϿ┘ç ϺÏ│Ϭ.
- ┘üÏ▒┘àÔÇî┘çϺ█î ┘à┘åÏ»┘äÏ¿Ï▒┘ê
┘àϼ┘à┘êÏ╣┘çÔÇî┘çϺ█î ┘à┘åÏ»┘äÏ¿Ï▒┘ê ϻϺÏ▒Ϻ█î ┘¥█î┌å█îÏ»┌»█î ϫϺÏÁ█î ┘çÏ│Ϭ┘åÏ». Ï▓┘àϺ┘å█î ┌®┘ç █î┌® ┘üÏ▒┘à ϡϺ┘äϬ█î ┘¥█î┌å█îÏ»┘ç ┘¥█îϻϺ ┘à█îÔÇî┌®┘åÏ» █îϺ Ï¿┘ç Ï╣ϿϺÏ▒Ϭ Ï»█î┌»Ï▒ Ï¿┘ç Ï╣┘åϺÏÁÏ▒ Ï«Ï▒Ï» ϬÏ┤┌®█î┘ä Ï»┘ç┘åÏ»┘ç ┌®┘ä ┘à█îÔÇîÏ▒Ï│Ï»Ïî ┘üÏ▒┘àÔÇî┘çϺ█î█î Ï¿Ï│█îϺÏ▒ ┘¥█î┌å█îÏ»┘ç Ϻ┘àϺ Ï»Ï▒ Ï╣█î┘å ϡϺ┘ä ┘à┘åÏ©┘à█î Ï▒Ϻ Ï¿┘ç ┘àϺ ┘à█îÔÇîÏ»┘çÏ» ┌®┘ç Ï»Ï▒ ϺÏ┤┌®Ïº┘ä Ï▓█îÏ▒ ┘ê ┘å┘à┘ê┘å┘çÔÇî┘çϺ█î ┘¥█îÏ┤ÔÇî┘üÏ▒Ï ┘ê Ïó┘àϺϻ┘ç Ï»Ï▒ ┘üÏ▒┌®Ï¬Ïº┘ä Ϻ┌®Ï│┘¥┘ä┘êÏ▒Ï▒ ┌»Ï░ϺÏ┤Ϭ┘ç Ï┤Ï»┘çÔÇîϺÏ│Ϭ.
- ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä Ï»Ï▒ ┘à┘åϺϩÏ▒ ÏÀÏ¿█îÏ╣█î
Ϻ█î┘å ┘üÏ▒┘àÔÇî┘çϺ ┘ç┘àϺ┘åÔÇîÏÀ┘êÏ▒ ┌®┘ç ϺÏ▓ ϺÏ│┘à Ïó┘åÔÇî┘çϺ ┘¥█îϻϺÏ│Ϭ ϻϺÏ▒Ϻ█î ┘üÏ▒┘à█î ÏÀÏ¿█îÏ╣█î ┘çÏ│Ϭ┘åÏ» (Ï╣Ï»┘à Ï»Ï│ϬϿÏ▒Ï» Ï»Ï│Ϭ Ï¿Ï┤Ï▒). Ï┤Ϻ█îÏ» Ï¿Ï│█îϺÏ▒ Ï»Ï▒ Ï╣┌®ÏºÏ│█î ┘àÏ╣┘àϺÏ▒█î (Ï¿Ï▒Ϻ█î Ï╣┌®Ï│ ϺÏ▓ █î┌® Ï│┘ê┌ÿ┘ç) Ï¿┘ç █î┌® ┘à┘åÏ©Ï▒┘ç Ï¿Ï▒Ï«┘êÏ▒Ï» ┌®Ï▒Ï»┘ç ϿϺÏ┤█îÏ» ┌®┘ç Ï»Ï▒ Ï»┘êÏ▒Ï»Ï│Ϭ Ϭ┘¥┘çÔÇî┘çϺ ┘ê ┌®┘ê┘çÔÇî┘çϺ Ï»█îÏ»┘ç ┘à█îÔÇîÏ┤┘ê┘åÏ»Ïî Ï¿Ï» ┘å█îÏ│Ϭ ϿϻϺ┘å█îÏ» ┌®┘ç Ï«┘êÏ» Ϻ█î┘å ┘à┘åÏ©Ï▒┘ç ϻϺÏ▒Ϻ█î ┘üÏ▒┘à█î ┘üÏ▒┌®Ï¬Ïº┘ä ϿϺ ┘ç┘åÏ»Ï│┘ç ┘üÏ▒┌®Ï¬Ïº┘ä ┘éϺϿ┘ä Ï¡┘ä ϺÏ│Ϭ.
Ϻ┘ä┌»┘ê┘çϺ█î Ï▒┘ê█îÏ┤ ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î
Ϻ█îÏ»┘ç Ï«┘êÏ» ┘àϬÏ┤ϺϿ┘ç Ï»Ï▒ ϺÏÁ┘ä Ϭ┘êÏ│ÏÀ ┘äϺ█îÏ¿ÔÇî┘å█îϬÏ│ Ï¿Ï│ÏÀ ϻϺϻ┘ç Ï┤Ï». Ϻ┘ê ϡϬ█î Ï¿Ï│█îϺÏ▒█î ϺÏ▓ ϼÏ▓Ϫ█îϺϬ Ï▒Ϻ Ï¡┘ä ┌®Ï▒Ï». Ï»Ï▒ Ï│Ϻ┘ä █▒█©█À█▓ ┌®ÏºÏ▒┘ä ┘êϺ█îÏ▒Ï┤ϬÏ▒ϺÏ│ ┘àϽϺ┘ä█î ϺÏ▓ ϬϺϿÏ╣█î Ï▒Ϻ ┘¥█îϻϺ ┌®Ï▒Ï» ϿϺ ┘ê█î┌ÿ┌»█îÔÇî┘çϺ█î Ï║█îÏ▒ Ï¿ÏÁÏ▒█î ┌®┘ç Ï»Ï▒ ┘ç┘à┘ç ϼϺ ┘¥█î┘êÏ│Ϭ┘ç Ï¿┘êÏ» ┘ê┘ä█î Ï»Ï▒ ┘çÏ▒ ϼϺ ┘àÏ┤Ϭ┘é ┘¥Ï░█îÏ▒ ┘åÏ¿┘êÏ». ┌»Ï▒Ϻ┘ü Ϻ█î┘å ϬϺϿÏ╣ Ϻ┌®┘å┘ê┘å ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ┘åϺ┘à█îÏ»┘ç ┘à█îÔÇîÏ┤┘êÏ». Ï»Ï▒ Ï│Ϻ┘ä █▒█╣█░█┤ ┘ç┘ä┌»┘ç ┘ü┘ê┘å ┌®Ï« Ï¿┘ç ┘ç┘àÏ▒Ϻ┘ç Ï«┘äϺÏÁ┘çÔÇîϺ█î ϺÏ▓ ϬÏ╣Ï▒█î┘ü Ϭϡ┘ä█î┘ä█î ┘êϺ█îÏ▒Ï┤ϬÏ▒ϺÏ│Ïî ϬÏ╣Ï▒█î┘ü ┘ç┘åÏ»Ï│█îÔÇîϬÏ▒█î ϺÏ▓ ϬϺϿÏ╣ ┘àϬÏ┤ϺϿ┘ç ϺÏ▒ϺϪ┘ç ϻϺϻ ┌®┘ç ϡϺ┘äϺ Ï¿┘ç Ï¿Ï▒┘üϻϺ┘å┘ç ┌®Ï« ┘àÏ╣Ï▒┘ê┘ü ϺÏ│Ϭ. Ï»Ï▒ Ï│Ϻ┘ä █▒█╣█▒█Á ┘êϺ┌®┘ä┘ê Ï│Ï▒┘¥█î┘åÏ│┌®█î ┘àϽ┘äϽÏ┤ Ï▒Ϻ ┘ê Ï│Ϻ┘ä Ï¿Ï╣Ï» ┘üÏ▒Ï┤ÔÇîϺÏ┤ (┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î) Ï▒Ϻ Ï│ϺϫϬ. Ϻ█îÏ»┘ç ┘à┘åÏ¡┘å█îÔÇî┘çϺ█î Ï«┘êÏ» ┘àϬÏ┤ϺϿ┘ç Ϭ┘êÏ│ÏÀ ┘¥Ïº┘ê┘ä ┘¥█îÏ▒ ┘ä┘ê█î ┘àÏÀÏ▒Ï¡ Ï┤Ï» Ϻ┘ê Ï»Ï▒ ┘à┘éϺ┘ä┘ç ϺÏ┤ Ï»Ï▒ Ï│Ϻ┘ä █▒█╣█│█© ϿϺ Ï╣┘å┘êϺ┘å ┬½Ï│ÏÀÏ¡ █îϺ ┘à┘åÏ¡┘å█îÔÇî┘çϺ█î ┘üÏÂϺ█î█î ┘ê Ï│ÏÀ┘êÏ¡█î Ï┤Ϻ┘à┘ä Ï¿Ï«Ï┤ÔÇî┘çϺ█î ┘àϬÏ┤ϺϿ┘ç ┘åÏ│ϿϬ Ï¿┘ç ┌®┘ä┬╗ ┘à┘åÏ¡┘å█î ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î ϼϻ█îÏ»█î Ï▒Ϻ Ϭ┘êÏÁ█î┘ü ┌®Ï▒Ï» ┘à┘åÏ¡┘å█î ┘ä┘ê█î c. ┌»Ïª┘êÏ▒┌» ┌®Ïº┘åϬ┘êÏ▒ ┘àϽϺ┘ä█î ϺÏ▓ Ï▓█îÏ▒ ┘àϼ┘à┘êÏ╣┘çÔÇî┘çϺ█î Ï«ÏÀ Ï¡┘é█î┘é█î ϿϺ ┘ê█î┌ÿ┌»█îÔÇî┘çϺ█î ┘àÏ╣┘à┘ê┘ä ϺÏ▒ϺϪ┘ç ϻϺϻ. Ϻ█î┘å ┘àϼ┘à┘êÏ╣┘çÔÇî┘çϺ█î ┌®Ïº┘åϬ┘êÏ▒ Ϻ┌®┘å┘ê┘å Ï¿┘çÔÇîÏ╣┘å┘êϺ┘å ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä Ï┤┘åϺϫϬ┘ç ┘à█îÔÇîÏ┤┘ê┘åÏ». Ϻ┘êϺϫÏ▒ ┘éÏ▒┘å ┘å┘êÏ▓Ï»┘ç┘à ┘ê Ϻ┘êϺ█î┘ä ┘éÏ▒┘å Ï¿█îÏ│Ϭ┘à Ϭ┘êϺϿÏ╣ Ϭ┌®Ï▒ϺÏ▒ Ï┤┘ê┘åÏ»┘ç Ï»Ï▒ Ï│ÏÀÏ¡ ┘¥█î┌å█îÏ»┘ç Ϭ┘êÏ│ÏÀ ┘çϺ┘åÏ▒█î ┘¥┘êϺ┘å┌®ÏºÏ▒┘çÏî ┘ü┘ä█î┌®Ï│ ┌®┘äϺ█î┘åÏî ┘¥█îÏ▒ ┘üϺϬ┘ê ┘ê ┌»ÏºÏ│Ϭ┘ê┘å ϼ┘ê┘ä█îϺ Ï┤┘åϺϫϬ┘ç Ï┤Ï»┘ç Ï¿┘êÏ»┘åÏ». ϿϺ Ϻ█î┘å ┘êϼ┘êÏ» Ï¿Ï»┘ê┘å ┌®┘à┌® ┌»Ï▒Ϻ┘ü█î┌® Ï▒Ϻ█îϺ┘å┘çÔÇîϺ█î Ïó┘åÔÇî┘çϺ ┘åÏ│ϿϬ Ï¿┘ç ┘å┘àϺ█îÏ┤ Ï▓█îϿϺ█î█î Ï¿Ï│█îϺÏ▒█î ϺÏ▓ ϺÏ┤█îϺ█î█î ┌®┘ç ┌®Ï┤┘ü ┌®Ï▒Ï»┘ç Ï¿┘êÏ»┘åÏ»Ïî ┘üϺ┘éÏ» ┘àÏ╣┘å█î Ï¿┘êÏ»┘åÏ». Ï»Ï▒ Ï│Ϻ┘ä █▒█╣█Â█░ Ï¿┘å┘êϺ ┘à┘åÏ»┘äÏ¿Ï▒┘ê Ϭϡ┘é█î┘éϺϬ█î Ï▒Ϻ Ï»Ï▒ Ï┤┘åϺϫϬ Ï«┘êÏ»┘ç┘àϺ┘å┘åÏ»█î ÏÀ█î ┘à┘éϺ┘ä┘çÔÇîϺ█î ϿϺ Ï╣┘å┘êϺ┘å ┬½ÏÀ┘ê┘ä Ï│Ϻϡ┘ä Ï¿Ï▒█îϬϺ┘å█îϺ ┌å┘éÏ»Ï▒ ϺÏ│Ϭσ Ï«┘êÏ» ┘àϬÏ┤ϺϿ┘çÔÇîϺ█î Ïó┘àϺÏ▒█î ┘ê Ï¿Ï╣Ï» ┌®Ï│Ï▒█î┬╗ ÏóÏ║ϺÏ▓ ┌®Ï▒Ï». Ϻ█î┘å ┌®ÏºÏ▒┘çϺ Ï¿Ï▒ ϺÏ│ϺÏ│ ┌®ÏºÏ▒┘çϺ█î ┘¥█îÏ┤█î┘å Ï▒█î┌åϺÏ▒Ï»Ï│┘ê┘å ϺÏ│Ϭ┘êϺÏ▒ Ï¿┘êÏ». Ï»Ï▒ Ï│Ϻ┘ä █▒█╣█À█Á ┘à┘åÏ»┘äÏ¿Ï▒┘ê Ï¿Ï▒Ϻ█î ┘àÏ┤Ï«ÏÁ ┌®Ï▒Ï»┘å Ï┤Ϫ█î ┌®┘ç Ï¿Ï╣Ï» ┘çϺ┘êÏ│Ï»┘êÏ▒┘ü-Ï¿█îÏ│┌®┘ê█î┌å Ïó┘å Ï¿Ï▓Ï▒┌»ÔÇîϬÏ▒ ϺÏ▓ Ï¿Ï╣Ï» Ϭ┘ê┘¥┘ê┘ä┘ê┌ÿ█î┌® Ïó┘å ϺÏ│Ϭ ┌®┘ä┘à┘ç ┬½┘üÏ▒Ϻ┌®Ï¬Ïº┘ä┬╗ (┘üÏ▒Ϻ┌®Ï¬Ïº┘ä) Ï▒Ϻ ϺϿϻϺÏ╣ ┌®Ï▒Ï». Ϻ┘ê Ϻ█î┘å ϬÏ╣Ï▒█î┘ü Ï▒█îϺÏÂ█î Ï▒Ϻ ϺÏ▓ ÏÀÏ▒█î┘é Ï┤Ï¿█î┘çÔÇîÏ│ϺÏ▓█î ϫϺÏÁ Ï▒Ϻ█îϺ┘å┘çÔÇîϺ█î ϬÏ┤Ï▒█îÏ¡ ┌®Ï▒Ï».
┘üÏ▒Ϻ┌®Ï¬Ïº┘äÔÇî┘çϺ ϺÏ▓ ┘åÏ©Ï▒ Ï▒┘êÏ┤ ┘àÏÀϺ┘äÏ╣┘ç Ï¿┘ç ┘üÏ▒Ϻ┌®Ï¬Ïº┘äÔÇî┘çϺ█î ϼϿÏ▒█î ┘ê Ï¿Ï▒ ϫϺ┘äÔÇî┘çϺ█î ϺϡϬ┘àϺ┘äϺϬ█î Ϭ┘éÏ│█î┘à ┘à█îÔÇîÏ┤┘ê┘åÏ». ϺÏ▓ ÏÀÏ▒┘ü Ï»█î┌»Ï▒ ┘üÏ▒Ϻ┌®Ï¬Ïº┘äÔÇî┘çϺ █îϺ Ï«┘êÏ»┘ç┘àϺ┘å┘åÏ» Ϻ┘åÏ» self similarity █îϺ Ï«┘êÏ»┘åϺ┘ç┘à┌»Ï▒Ï» self affinity ┘çÏ│Ϭ┘åÏ». Ï»Ï▒ Ï«┘êÏ»┘ç┘àϺ┘å┘åÏ»█îÏî Ï┤┌®┘ä ϼÏ▓Ïí Ï┤ϿϺ┘çϬ ┘àÏ¡Ï│┘êÏ│█î Ï¿┘ç Ï┤┌®┘ä ┌®┘ä ϻϺÏ▒Ï». Ϻ█î┘å ϼÏ▓ÏíÏî Ï»Ï▒ ┘ç┘à┘ç ϼ┘çϺϬ Ï¿┘ç ┘åÏ│ϿϬ ϽϺϿϬ█î Ï▒Ï┤Ï» ┘à█îÔÇî┌®┘åÏ» ┘ê ┌®┘ä Ï▒Ϻ Ï¿┘ç ┘êϼ┘êÏ» ┘à█îÔÇîÏó┘êÏ▒Ï». Ϻ┘àϺ Ï»Ï▒ Ï«┘êÏ»┘åϺ┘ç┘à┌»Ï▒Ï»█î Ï┤┌®┘ä ϼÏ▓Ïí Ï»Ï▒ ┘ç┘à┘ç ϼ┘çϺϬ Ï¿┘ç ┘åÏ│ϿϬ ϽϺϿϬ█î Ï▒Ï┤Ï» ┘å┘à█îÔÇî┌®┘åÏ»Ïø ┘àϽ┘äϺ┘ï Ï»Ï▒ ┘à┘êÏ▒Ï» Ï▒┘êϻϫϺ┘å┘çÔÇî┘çϺ ┘ê Ï¡┘êÏÂ┘çÔÇî┘çϺ█î ÏóÏ¿Ï▒█îÏ▓ Ï¿Ï╣Ï» ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î ÏÀ┘ê┘ä█î ┘àϬ┘üϺ┘êϬ ϺÏ▓ Ï¿Ï╣Ï» ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î Ï╣Ï▒ÏÂ█î ϺÏ│Ϭ Vx = █░. █À█▓ÔÇô█░. █À█┤ ┘ê Vy = █░. █Á█▒ÔÇô█░. █Á█▓ (Ï│Ϻ┘¥┘ê┌ÿ┘å█î┌®┘ê┘ü ┘ê ┘ü┘ê┘ü┘ê┘äϺÏî █▒█╣█╣█│) ϺÏ▓ Ϻ█î┘åÔÇîÏ▒┘ê Ï┤┌®┘ä Ï¡┘êÏÂ┘ç ÏóÏ¿Ï▒█îÏ▓ ┌®Ï┤█îÏ»┘çÔÇîϬÏ▒ ϺÏ▓ Ï▓█îÏ▒ Ï¡┘êÏÂ┘çÔÇî┘çϺ█î Ï»Ï▒┘ê┘å Ï¡┘êÏÂ┘çÔÇî ϺÏ│Ϭ. Ï¿┘ç Ï«┘êÏ»┘ç┘àϺ┘å┘åÏ»█î ┘ç┘àÏ│Ϻ┘å┌»Ï▒Ï» ┘à█îÔÇî┌»┘ê█î┘åÏ». Ï¿┘ç Ï«┘êÏ» ┘åϺ┘ç┘à┌»Ï▒Ï»█î ┘åϺ┘ç┘àÏ│Ϻ┘å┌»Ï▒Ï» ┘à█îÔÇî┌»┘ê█î┘åÏ».
ÏÀÏ¿┘é┘çÔÇîÏ¿┘åÏ»█î
┘üÏ▒Ϻ┌®Ï¬Ïº┘äÔÇî┘çϺ ┘ç┘à┌å┘å█î┘å Ï¿Ï▒ ϺÏ│ϺÏ│ Ï«┘êÏ»-┘ç┘àϺ┘å┘åÏ»█î ÏÀÏ¿┘é┘çÔÇîÏ¿┘åÏ»█î ┘à█îÔÇîÏ┤┘ê┘åÏ». Ï│┘ç ┘å┘êÏ╣ Ï«┘êÏ» ┘ç┘àϺ┘å┘åÏ»█î ┘êϼ┘êÏ» ϻϺÏ▒Ï»:
- Ï«┘êÏ» ┘ç┘àϺ┘å┘åÏ»█î Ï»┘é█î┘é ÔÇô Ϻ█î┘å ┘é┘ê█îÔÇîϬÏ▒█î┘å ┘å┘êÏ╣ Ï«┘êÏ» ┘ç┘àϺ┘å┘åÏ»█î ϺÏ│Ϭ.
┌»Ï│ϬÏ▒Ï┤ Ï▒┘ê Ï¿┘ç Ï▒Ï┤Ï» Ï▒┘ê█î┌®Ï▒Ï» Ϭ┌®ÔÇî┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î (┘à┘ê┘å┘ê┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î) Ϻϫ█îÏ▒Ïî ϻϺϻ┘çÔÇî┘çϺ Ï▒Ϻ ϿϺ ┘àϼ┘à┘êÏ╣┘ç ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█îÏî Ï¿┘ç ϼϺ█î Ï¿Ï╣Ï» ┘à┘å┘üÏ▒Ï» ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î Ϭ┘êÏÁ█î┘ü ┘à█îÔÇî┌®┘åÏ». Ϻ█î┘å ┘àϼ┘à┘êÏ╣┘ç ÏÀ█î┘ü ┌å┘åÏ»┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î multifractal spectrum ┘åϺ┘à█îÏ»┘ç ┘à█îÔÇîÏ┤┘êÏ» ┘ê Ï▒┘êÏ┤ Ϭ┘êÏÁ█î┘ü ϬÏ║█î█îÏ▒┘¥Ï░█îÏ▒█î Ï¿Ï▒ ϺÏ│ϺÏ│ ÏÀ█î┘üÔÇîÏ│┘åϼ█î ┌å┘åÏ»┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î Ï¿┘ç Ïó┘åϺ┘ä█îÏ▓ ┌å┘åÏ»┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î ┘àÏ╣Ï▒┘ê┘ü ϺÏ│Ϭ (┘üÏ▒█îÏ┤ ┘ê ┘¥ÏºÏ▒█îÏ│█îÏî █▒█╣█©█Á). Ï▒┘êÏ┤ ┌å┘åÏ» ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î Ï¿┘ç Ϻ┘åϻϺÏ▓┘ç Ï«┘êÏ»┘ç┘àϺ┘å┘åÏ»█î Ïó┘àϺÏ▒█î Ï»┘äϺ┘äϬ ϻϺÏ▒Ï» ┌®┘ç ┘à█îÔÇîϬ┘êϺ┘åÏ» Ï¿┘ç ÏÁ┘êÏ▒Ϭ ϬÏ▒┌®█îÏ¿█î ϺÏ▓ ┘àϼ┘à┘êÏ╣┘çÔÇî┘çϺ█î Ï¿┘çÔÇî┘ç┘à Ϭ┘å█îÏ»┘ç ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î[█│] ┘àÏÀϺϿ┘é ϿϺ ┘å┘àϺ█î ┘à┘é█îϺÏ│ÔÇî┌»Ï░ϺÏ▒█î ┘å┘àϺ█îÏ┤ ϻϺϻ┘ç Ï┤┘êÏ». ϬÏ▒┌®█îÏ¿█î ϺÏ▓ ┘ç┘à┘ç ┘àϼ┘à┘êÏ╣┘çÔÇî┘çϺ█î ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î ÏÀ█î┘ü ┌å┘åÏ» ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█îÔÇîϺ█î Ï▒Ϻ Ϻ█îϼϺϻ ┘à█îÔÇî┌®┘åÏ» ┌®┘ç ϬÏ║█î█îÏ▒┘¥Ï░█îÏ▒█î ┘ê ┘åϺ┘ç┘à┌»┘å█î ┘àϬÏ║█îÏ▒ ┘à┘êÏ▒Ï» ┘àÏÀϺ┘äÏ╣┘ç Ï▒Ϻ ┘àÏ┤Ï«ÏÁ ┘à█îÔÇî┌®┘åÏ». ┘àÏ▓█îϬ Ï▒┘ê█î┌®Ï▒Ï» ┌å┘åÏ» ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î Ϻ█î┘å ϺÏ│Ϭ ┌®┘ç ┘¥ÏºÏ▒Ϻ┘àϬÏ▒┘çϺ█î ┌å┘åÏ»┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î ┘à█îÔÇîϬ┘êϺ┘å┘åÏ» ┘àÏ│Ϭ┘é┘ä ϺÏ▓ Ϻ┘åϻϺÏ▓┘ç ┘à┘êÏÂ┘êÏ╣ ┘à┘êÏ▒Ï» ┘àÏÀϺ┘äÏ╣┘ç ϿϺÏ┤┘åÏ».[█┤]
┌®ÏºÏ▒Ï¿Ï▒Ï»┘çϺ
ϺÏ▓ ┘üÏ▒Ϻ┌®Ï¬Ïº┘äÔÇî┘çϺ Ï¿┘ç ┘à┘åÏ©┘êÏ▒ ÏóÏ│Ϻ┘åÔÇîÏ│ϺÏ▓█î Ï»Ï▒ ┌®ÏºÏ▒┘çϺ█î ┘êϺϿÏ│Ϭ┘ç Ï¿┘ç ┘àÏ»┘äÔÇîÏ│ϺÏ▓█î ┘¥█î┌å█îÏ»┌»█î Ï»Ï▒ Ï▓┘à█î┘å┘çÔÇî┘çϺ█î ┌»┘ê┘åϺ┌»┘ê┘å Ï╣┘ä┘à█î ┘ê ┘à┘ç┘åÏ»Ï│█î ϺÏ│Ϭ┘üϺϻ┘ç ┘à█îÔÇîÏ┤┘êÏ». ϺÏ▓ Ï▓┘à█î┘å┘çÔÇî┘çϺ█î ┘à┘ç┘à ┌®ÏºÏ▒Ï¿Ï▒Ï»█î ┌»Ï▓█î┘å┘çÔÇî┘çϺ█î Ï▓█îÏ▒ Ï▒Ϻ ┘à█îÔÇîϬ┘êϺ┘å Ï¿Ï▒Ï┤┘àÏ▒Ï»:
Ï▒ϺϿÏÀ┘ç ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ┘ê ┘àÏ╣┘àϺÏ▒█î
Ϻ┘åÏ│Ϻ┘åÔÇî┘çϺ Ï»Ï▒ Ï▒┘êÏ▓┌»ÏºÏ▒ ┘éÏ»█î┘à Ï»Ï▒ ÏÀÏ¿█îÏ╣Ϭ ┘à█îÔÇîÏ▓█îÏ│Ϭ┘åÏ» ┘ê ┘àϺ┘å┘åÏ» Ϻ┘åÏ│Ϻ┘å Ï»┘êÏ▒┘ç ┘å┘ê█î┘åÏî ϿϺ ÏÀÏ¿█îÏ╣Ϭ Ï¿█î┌»Ïº┘å┘ç ┘åÏ¿┘êÏ»┘åÏ»Ïî Ï¿┘ç Ϻ█î┘å Ï▒┘ê ┘àÏ╣┘àϺÏ▒█îÏ┤Ϻ┘å ϿϺ ┘åÏ©┘à ÏÀÏ¿█îÏ╣Ϭ Ï¿┘êÏ». Ïó┘åÔÇî┘çϺ Ï¿┘ç Ϻ█î┘å ┘üÏ▒┘å┘êÏ» ┌®┘ç Ï»Ï▒ ÏÀÏ¿█îÏ╣Ϭ Ï▒Ï┤Ï» ┘à█îÔÇî█îϺ┘üϬ┘åÏ»Ïî ÏÂ┘à█îÏ▒ ┘åϺϫ┘êÏ»Ïó┌»Ïº┘çÏ┤Ϻ┘å ┘å█îÏ▓ ϿϺ ┘åÏ©┘à ÏÀÏ¿█îÏ╣Ϭ- █îÏ╣┘å█î ϿϺ ┘åÏ©┘à ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä- Ï▒Ï┤Ï» ┘à█îÔÇî█îϺ┘üϬÏî Ï»Ï▒ ┘åϬ█îϼ┘ç Ï│ϺϫϬ┘çÔÇî┘çϺ█îÏ┤Ϻ┘å ┘å█îÏ▓ ϻϺÏ▒Ϻ█î ┘åÏ©┘à ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ┘à█îÔÇîÏ¿┘êÏ».
┘àÏÀϺ┘äÏ╣┘ç ┘ç┘åÏ»Ï│┘ç ϿϺ█îÏ» Ï¿┘ç ÏÀÏ▒Ϻϡ ┌®┘à┌® ┌®┘åÏ» ┌®┘ç Ï¿┘ç Ï»Ï▒┌® Ï¿┘çϬÏ▒█î ϺÏ▓ ϼÏ▒█îϺ┘å Ï▒█îÏ▓┌»Ïº┘å (ϼÏ▓Ϫ█îϺϬ) Ï»Ï▒ ┘¥█îÏ▒Ϻ┘à┘ê┘å ┘àϺ ┘ê ϼ┘çϺ┘å ÏÀÏ¿█îÏ╣█î Ï»Ï│Ϭ █îϺϿϻ. ┘ê█î┌ÿ┌»█îÔÇî┘çϺ█î ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î █î┌® Ïó┘à█îÏ▓┘ç ┘àÏ╣┘àϺÏ▒█î Ï»Ï▒ ┘¥█î┘êÏ│Ϭ┌»█î Ï▓┘åϼ█îÏ▒┘êϺÏ▒ Ï▒█îÏ▓┌»Ïº┘å ϺÏ│Ϭ. Ϻ█î┘å ┘¥█î┘êÏ│Ϭ┌»█î Ï▓┘åϼ█îÏ▒┘êϺÏ▒ Ï¿Ï▒Ϻ█î ϼÏ░ϺϿ█îϬ ┘àÏ╣┘àϺÏ▒█î ┘äϺÏ▓┘à ϺÏ│Ϭ. ┘ç┘å┌»Ïº┘à█î ┌®┘ç Ϭ┘å┘ê┘à█î (Ï┤Ï«ÏÁ█î) Ï¿┘ç █î┌® Ï│ϺϫϬ┘àϺ┘å ┘åÏ▓Ï»█î┌® ┘ê Ï│┘¥Ï│ Ï¿┘ç Ïó┘å ┘êϺÏ▒Ï» ┘à█îÔÇîÏ┤┘êÏ» ┘ç┘à█îÏ┤┘ç ϿϺ█îÏ» ┘à┘é█îϺÏ│ ┌®┘ê┌å┌®Ï¬Ï▒ Ï»█î┌»Ï▒█î ┘ç┘àÏ▒Ϻ┘ç ϿϺ Ï▒█îÏ▓┌»Ïº┘å ϼÏ░ϺϿ ┘êϼ┘êÏ» ϻϺÏ┤Ϭ┘ç ϿϺÏ┤Ï» ϬϺ ┘àÏ╣┘åϺ█î ┌®┘ä█î Ïó┘à█îÏ▓┘ç Ï▒Ϻ Ï¿█îϺ┘å ┌®┘åÏ» ┌®┘ç Ϻ█î┘å █î┌® Ϻ█îÏ»┘ç ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ϺÏ│Ϭ.[█▓][█Á][█Â]
┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ┘ê ┘ç┘åÏ▒
Ï»Ï▒ ┘ç┘åÏ▒ Ï»┘êÏ▒Ϻ┘åÔÇî┘çϺ█î ┘àϫϬ┘ä┘ü Ï│ϺϫϬϺÏ▒┘çϺ ┘ê ┌»┘ê┘å┘çÔÇî┘çϺ ┘ê ϡϬ█î ┘å┘éϺÏ┤█îÔÇî┘çϺ█î ┌»┘ê┘åϺ┌»┘ê┘å█î Ï▒Ϻ ϺÏ▓ ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ┘à█îÔÇîÏ¿█î┘å█î┘à. Ï»Ï▒ Ϻ█î┘å Ï▓┘à█î┘å┘ç Ï¿┘ç Ï░┌®Ï▒ █▓ ┘å┘à┘ê┘å┘ç Ï¿Ï│┘åÏ»┘ç ┘à█îÔÇî┌®┘å█î┘à.
- ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä █îϺ ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä Ï»Ï▒ ┘ç┘åÏ»Ï│┘ç ┘àÏ╣┘àϺÏ▒█î Ϻ█îÏ▒Ϻ┘å█î-ϺÏ│┘äϺ┘à█îÏî ┌®┘ç Ï¿┘çϬÏ▒█î┘å ┘å┘à┘ê┘å┘çÔÇî┘çϺ█î Ïó┘å ┘à┘éÏ▒┘åÏ│ÔÇî┘çϺ█î ┘àÏ│ϼϻ Ï┤Ϻ┘ç ϺÏÁ┘ü┘çϺ┘å ┘ê ÏÀÏ▒Ï¡ ┌®ÏºÏ┤█î ┌®ÏºÏ▒█î Ï▓█îÏ▒ ┌»┘åÏ¿Ï» ┘àÏ│ϼϻ Ï┤█îÏ« ┘äÏÀ┘üÔÇîϺ┘ä┘ä┘ç Ï»Ï▒ ┘à█îϻϺ┘å ┘å┘éÏ┤ ϼ┘çϺ┘å ϺÏÁ┘ü┘çϺ┘å ϺÏ│Ϭ.
- ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä Ï»Ï▒ ┘ç┘åÏ▒ Ïó┘üÏ▒█î┘éϺ
- ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä Ï▒Ϻ Ï»Ï▒ ÏóϽϺÏ▒ ┘å┘éϺÏ┤Ϻ┘å█î ┌å┘ê┘å ϼ┌®Ï│┘ê┘å ┘¥┘ê┘äϺ┌® ┘ê ┘äϺÏ▒█î ┘¥┘ê┘åÏ▓. ϻϺ┘åÏ┤┘à┘åϻϺ┘å Ï╣┘ä┘ê┘à ϺÏ╣ÏÁϺϿ Ï┤┘åϺϫϬ█î Ï»Ï▒█îϺ┘üϬ┘ç Ϻ┘åÏ» ┌®┘ç ┘üÏ▒Ϻ┌®Ï¬Ïº┘äÔÇî┘çϺ█î ϼ┌®Ï│┘ê┘å ┘¥┘ê┘äϺ┌® ┘ç┘àϺ┘å ┘êϺ┌®┘åÏ┤█î Ï▒Ϻ Ï»Ï▒ Ϻ┘üÏ▒Ϻϻ Ϻ█îϼϺϻ ┘à█îÔÇî┌®┘åÏ» ┌®┘ç ┘üÏ▒Ϻ┌®Ï¬Ïº┘äÔÇî┘çϺ█î ┘à┘êϼ┘êÏ» Ï»Ï▒ ÏÀÏ¿█îÏ╣Ϭ ┘ê ┘üÏ▒Ϻ┌®Ï¬Ïº┘äÔÇî┘çϺ█î Ϭ┘ê┘ä█îÏ» Ï┤Ï»┘ç Ϭ┘êÏ│ÏÀ Ï▒Ϻ█îϺ┘å┘ç Ϻ█îϼϺϻ ┘à█îÔÇî┌®┘åÏ». ┘ü█îÏ▓█î┌®Ï»Ïº┘å█î Ï¿┘ç ┘åϺ┘à Ï▒█î┌åϺÏ▒Ï» Ϭ█î┘ä┘êÏ▒Ïî Ϻ┘ä┌»┘ê┘çϺ█î ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä█î ┌®ÏºÏ▒┘çϺ█î ϼ┌®Ï│┘ê┘å ┘¥┘ê┘äϺ┌® Ï▒Ϻ Ï¿Ï▒Ï▒Ï│█î ┌®Ï▒Ï»┘çÔÇîϺÏ│Ϭ. Ϭ█î┘ä┘êÏ▒ ┘åϬ█îϼ┘ç ┌»Ï▒┘üϬ ┌®┘ç ϺϿÏ╣Ϻϻ ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ┘å┘éϺÏ┤█îÔÇî┘çϺ█î ┘éÏÀÏ▒┘ç Ϻ█î Ϻ┘ê┘ä█î┘ç Ϭ█î┘ä┘êÏ▒ ϼ┌®Ï│┘ê┘å ┘¥┘ê┘äϺ┌®Ïî ϿϺ Ïó┘å┌å┘ç Ï»Ï▒ ÏÀÏ¿█îÏ╣Ϭ █îϺ┘üϬ ┘à█îÔÇîÏ┤┘êÏ» ┘àÏÀϺϿ┘éϬ ϻϺÏ▒Ï». Ï¿┘ç Ï╣┘å┘êϺ┘å ┘àϽϺ┘äÏî █î┌® ┘å┘éϺÏ┤█î ┘ê█îÏî ϻϺÏ▒Ϻ█î ϺϿÏ╣Ϻϻ ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä █▒┘½█┤█ÁÏî Ï┤Ï¿█î┘ç Ï¿Ï│█îϺÏ▒█î ϺÏ▓ Ï«ÏÀ┘êÏÀ Ï│Ϻϡ┘ä█î ϺÏ│Ϭ. ┘éÏÀÏ¿ÔÇî┘çϺ█î ÏóÏ¿█îÏî █î┌®█î ϺÏ▓ ÏóÏ«Ï▒█î┘å ┘å┘éϺÏ┤█îÔÇî┘çϺ█î ┘éÏÀÏ▒┘ç Ϻ█î ϼ┌®Ï│┘ê┘å ┘¥┘ê┘äϺ┌® ┌®┘ç Ϻ┌®┘å┘ê┘å Ï¿█îÏ┤ ϺÏ▓ █│█░ ┘à█î┘ä█î┘ê┘å Ï»┘äϺÏ▒ ϺÏ▒Ï▓Ï┤ ϻϺÏ▒Ï»Ïî Ï»Ï▒ ┘àϻϬ Ï┤Ï┤ ┘àϺ┘ç ┘å┘éϺÏ┤█î Ï┤Ï»┘çÔÇîϺÏ│Ϭ ┘ê ϻϺÏ▒Ϻ█î ϿϺ┘äϺϬÏ▒█î┘å ϺϿÏ╣Ϻϻ ┘üÏ▒Ϻ┌®Ï¬Ïº┘ä ϺÏ▓ Ï¿█î┘å ┘å┘éϺÏ┤█îÔÇî┘çϺ█î ϼ┌®Ï│┘ê┘å ┘¥┘ê┘äϺ┌® ϺÏ│Ϭ ┌®┘ç Ϭ█î┘ä┘êÏ▒ ÏóÏ▓┘àϺ█îÏ┤ ┌®Ï▒Ï»┘çÔÇîϺÏ│Ϭ: █▒┘½█À█▓.
- Ï»Ï▒ Ï│Ϻ┘ä █▒█©█▓█░Ïî ┌®ÏºÏ¬Ï│┘êÏ┤█î┌®Ïº ┘ç┘ê┌®┘êÏ│Ϻ█îÏî[█À] ┘ç┘åÏ▒┘à┘åÏ» ┌ÿϺ┘¥┘å█îÏî ϺϽÏ▒ ┬½┘à┘êϼ Ï╣Ï©█î┘à ┌®Ïº┘åϺ┌»Ïº┘êϺ┬╗ Ï▒Ϻ Ï«┘ä┘é ┌®Ï▒Ï»Ïî ϼϺ█î█î ┌®┘ç ┘à┘êϼ Ï¿Ï▓Ï▒┌» Ϻ┘é█îϺ┘å┘êÏ│ Ï¿┘ç ┘à┘êϼÔÇî┘çϺ█î ┌®┘ê┌å┌®Ï¬Ï▒ ┘ê ┌®┘ê┌å┌®ÔÇîϬÏ▒Ïî █îÏ╣┘å█î ┘à┘êϼÔÇî┘çϺ█î ┘àÏ┤ϺϿ┘ç Ï«┘êÏ»Ïî Ï┤┌®Ï│Ϭ┘ç ┘à█îÔÇîÏ┤┘êÏ».
┘à┘åϺϿÏ╣ ┘ê ┘¥Ïº┘å┘ê█îÏ│
ϼÏ│ϬϺÏ▒┘çϺ█î ┘êϺϿÏ│Ϭ┘ç
┘¥█î┘ê┘åÏ» Ï¿┘ç Ï¿█îÏ▒┘ê┘å
|
|---|
| Ï┤┌®┘äÔÇî┘çϺ | | |
|---|
| ÏóϽϺÏ▒ ┘ç┘åÏ▒█î | |
|---|
| Ï│ϺÏ▓┘çÔÇî┘çϺ | |
|---|
| ┘ç┘åÏ▒┘à┘åϻϺ┘å | Ï▒┘åÏ│Ϻ┘åÏ│ | |
|---|
┘éÏ▒┘å ┘å┘êÏ▓Ï»┘ç┘à-Ï¿█îÏ│Ϭ┘à | |
|---|
┘àÏ╣ϺÏÁÏ▒ | |
|---|
|
|---|
| ┘à┘üϺ┘ç█î┘à | |
|---|
| ┘åÏ©Ï▒█î┘çÔÇî┘¥Ï▒ϻϺÏ▓Ϻ┘å | ϿϺÏ│ϬϺ┘å | |
|---|
Ï▒┘åÏ│Ϻ┘åÏ│ | |
|---|
┘àÏ»Ï▒┘å | |
|---|
|
|---|
| Ϻ┘åϬÏ┤ϺÏ▒ϺϬ | |
|---|
| Ï│ϺÏ▓┘àϺ┘åÔÇî┘çϺ | |
|---|
| ϼÏ│ϬϺÏ▒┘çϺ█î ┘êϺϿÏ│Ϭ┘ç | |
|---|
|
|
|---|
| Ϻ┘ä┌»┘ê┘çϺ | | |
|---|
| Ï»┘äϺ█î┘ä | |
|---|
| Ϻ┘åÏ│Ϻ┘åÔÇî┘çϺ | |
|---|
| ϼÏ│ϬϺÏ▒┘çϺ█î ┘êϺϿÏ│Ϭ┘ç | |
|---|