ØŊØą ØģاŲ ÛąÛļÛĩÛąØ ØŽŲØąØŽ ÚŊاØĻØąÛŲ اØģØŠŲÚĐØģ Ų
ØđاØŊŲŲâØ§Û ØąØ§ ÚĐŲ اÚĐŲŲŲ ØĻŲ ŲاŲ
ŲاŲŲŲ اØģØŠŲÚĐØģ ØīŲاØŪØŠŲ Ų
Û ØīŲØŊØ ØĻØąØ§Û ŲÛØąŲÛ Ø§ØĩØ·ÚĐاÚĐ - ÚĐŲ ŲÛØąŲÛ ÚĐØīØī ŲÛØē ŲاŲ
ÛØŊŲ Ų
Û ØīŲØŊ - اØģØŠØŪØąØ§ØŽ ÚĐØąØŊ ÚĐŲ ØĻØą ا؎ØģاŲ
ÚĐØąŲÛ ØĻا اØđØŊاØŊ ØąÛŲŲŲØŊØē ØĻØģÛØ§Øą ÚĐŲÚÚĐ ØŊØą ÛÚĐ ØŽØąÛاŲ اØģØŠŲÚĐØģ اØđŲ
اŲ Ų
Û ØīŲØŊ. [Ûą] ŲاŲŲŲ اØģØŠŲÚĐØģ ØĻا ØŲ ØØŊ ØŽØąÛاŲ اØģØŠŲÚĐØģ ØĻØąØ§Û Ø§ØđØŊاØŊ ÚĐŲÚÚĐ ØąÛŲŲŲØŊØē Ų
ØđاØŊŲا؊ ŲاŲÛØą-اØģØŠŲÚĐØģ ØĻŲ ØŊØģØŠ Ų
Û ØĒÛØŊ. [Ûē]
ØŠØđØąÛŲ ŲاŲŲŲ
ŲÛØąŲÛ ÚŊØąØ§ŲâØąŲÛ ØąŲÛ ÛÚĐ ÚĐØąŲ ÚĐŲÚÚĐ ÚĐŲ ØŊØą ÛÚĐ ØīØ§ØąŲ ØĻا ÚŊØąØ§ŲâØąŲÛ ØØąÚĐØŠ Ų
Û ÚĐŲØŊ ØĻŲ ØĩŲØąØŠ ØēÛØą ØĻŲ ØŊØģØŠ Ų
Û ØĒÛØŊ:

؎اÛÛ ÚĐŲ:
- F d ŲÛØąŲÛ Ø§ØĩØ·ÚĐاÚĐ Ø§ØģØŠ - Ų
ØđØąŲŲ ØĻŲ ÚĐØīØī اØģØŠŲÚĐØģ - ÚĐŲ ØĻØą ØģØ·Ø Ų
ØīØŠØąÚĐ ØĻÛŲ ØīØ§ØąŲ Ų Ø°ØąŲ اØŦØą Ų
Û ÚĐŲØŊ.
- ÎžØ ÚŊØąØ§ŲâØąŲÛ ØŊÛŲاŲ
ÛÚĐÛ Ø§ØģØŠ. (ØĻØđØķÛ ŲŲÛØģŲØŊÚŊاŲ اØē ŲŲ
اØŊ η اØģØŠŲاØŊŲ Ų
Û ÚĐŲŲØŊ).
- R ØīØđاØđ ØŽØģŲ
ÚĐØąŲÛ Ø§ØģØŠ.
- v ØģØąØđØŠ ØŽØąÛاŲ ŲØģØĻØŠ ØĻŲ ØŽØģŲ
اØģØŠ.
ØŊØą ØŊØģØŠÚŊاŲ ØĻÛŲâاŲŲ
ŲŲÛ ÛÚĐاŲØ§Ø Fd ØĻØą ØØģØĻ ŲÛŲØŠŲ (= kg ms -2 )Ø Îž ØĻØą ØØģØĻ ŲūاØģÚĐاŲ ØŊØą ØŦاŲÛŲ (= kg m -1 s -1 )Ø R ØĻØą ØØģØĻ Ų
ØŠØąØ Ų v ØĻØą ØØģØĻ Ų
ØŠØą ØĻØą ØŦاŲÛŲ ØŊاØŊŲ Ų
Û ØīŲØŊ.
ŲاŲŲŲ اØģØŠŲÚĐØģ Ų
ŲØąŲØķا؊ ØēÛØą ØąØ§ ØĻØąØ§Û ØąŲØŠØ§Øą ÛÚĐ Ø°ØąŲ ØŊØą ÛÚĐ ØīØ§ØąŲ ØĻÛاŲ Ų
Û ÚĐŲØŊ:
- ØŽØąÛاŲ ØĒØąØ§Ų
- Ø°ØąØ§ØŠ ÚĐØąŲÛ
- Ų
ŲاØŊ ŲŲ
ÚŊŲ (ÛÚĐŲŲاØŪØŠ ØŊØą ØŠØąÚĐÛØĻ).
- ØģØ·ŲØ ØĩاŲ
- Ø°ØąØ§ØŠ ØĻا ÛÚĐØŊÛÚŊØą ØŠØŊاØŪŲ ŲØŊØ§ØąŲØŊ.
ØĻØąØ§Û Ų
ŲŲÚĐŲŲâŲا اØē ŲاŲŲŲ اØģØŠŲÚĐØģ ØĻØąØ§Û ØŠØđÛÛŲ ØīØđاØđ Ų ŲØ·Øą اØģØŠŲÚĐØģ اØģØŠŲاØŊŲ Ų
Û ØīŲØŊ.
ŲاØØŊ ØŊØģØŠÚŊاŲ ŲاØØŊŲØ§Û ØģاŲØŠÛŲ
ØŠØąâÚŊØąŲ
âØŦاŲÛŲ ÚŊØąØ§ŲâØąŲÛ ØģÛŲŲ
ا؊ÛÚĐÛ ŲūØģ اØē ÚĐØ§Øą اŲ "اØģØŠŲÚĐØģ" ŲاŲ
ÛØŊŲ ØīØŊ.
ÚĐØ§ØąØĻØąØŊŲا
ŲاŲŲŲ اØģØŠŲÚĐØģ اØģاØģ ŲÛØģÚĐŲŲ
ØŠØą ØģŲŲØ· ÚĐØąŲ اØģØŠ ÚĐŲ ØŊØą ØĒŲ ØīØ§ØąŲ ØŊØą ÛÚĐ ŲŲŲŲ ØīÛØīŲâØ§Û ØđŲ
ŲØŊÛ ØģاÚĐŲ اØģØŠ. ÚĐØąŲâØ§Û ØĻا اŲØŊاØēŲ Ų ÚÚŊاŲÛ ØīŲاØŪØŠŲ ØīØŊŲ ا؎اØēŲ ØŊØ§ØąØŊ اØē Ø·ØąÛŲ Ų
اÛØđ ŲūاÛÛŲ ØĻÛاÛØŊ. اÚŊØą ØĻŲ ØŊØąØģØŠÛ Ø§ŲØŠØŪاØĻ ØīŲØŊØ ØĻŲ ØģØąØđØŠ ØØŊ Ų
ÛâØąØģØŊØ ÚĐŲ Ų
ÛâØŠŲاŲØŊ ØĻا Ų
ØŊØŠ ØēŲ
اŲÛ ÚĐŲ Ø·ŲŲ Ų
ÛâÚĐØīØŊ ؊ا اØē ØŊŲ ØđŲاŲ
ØŠ Ų
ŲØŽŲØŊ ØąŲÛ ŲŲŲŲ ØąØŊ ØīŲØŊØ Ø§ŲØŊاØēŲ ÚŊÛØąÛ ØīŲØŊ. ØĻØąØ§Û ØīØ§ØąŲâŲØ§Û Ų
ا؊ Ų
ÛâØŠŲاŲ اØē ØģŲØŽØī اŲÚĐØŠØąŲŲÛÚĐÛ Ø§ØģØŠŲاØŊŲ ÚĐØąØŊ. ØĻا ØŊاŲØģØŠŲ ØģØąØđØŠ ØØŊØ Ø§ŲØŊاØēŲ Ų ÚÚŊاŲÛ ÚĐØąŲ Ų ÚÚŊاŲÛ Ų
اÛØđØ Ų
ÛâØŠŲاŲ اØē ŲاŲŲŲ اØģØŠŲÚĐØģ ØĻØąØ§Û Ų
ØاØģØĻŲ ÚŊØąØ§ŲâØąŲÛ ØīØ§ØąŲ اØģØŠŲاØŊŲ ÚĐØąØŊ. ÛÚĐ ØģØąÛ ØĻŲØĻØąÛŲÚŊ ŲŲŲاØŊÛ ØĻا ŲØ·ØąŲØ§Û Ų
ØŪØŠŲŲ Ų
ØđŲ
ŲŲاŲ ØŊØą ØĒØēŲ
اÛØī ÚĐŲاØģÛÚĐ ØĻØąØ§Û ØĻŲØĻŲØŊ ØŊŲØŠ Ų
ØاØģØĻا؊ اØģØŠŲاØŊŲ Ų
ÛâØīŲØŊ. ØŊØą ØĒØēŲ
اÛØī Ų
ØŊØąØģŲ اØē ÚŊŲÛØģÛØąÛŲ Ûا ØđØĩØ§ØąŲ Ø·ŲاÛÛ ØĻŲ ØđŲŲاŲ Ų
اÛØđ اØģØŠŲاØŊŲ Ų
ÛâØīŲØŊ Ų اÛŲ ØŠÚĐŲÛÚĐ ØĻŲ ØĩŲØąØŠ ØĩŲØđØŠÛ ØĻØąØ§Û ØĻØąØąØģÛ ÚŊØąØ§ŲâØąŲÛ Ų
اÛØđا؊ Ų
ŲØąØŊ اØģØŠŲاØŊŲ ØŊØą ŲØąØĒÛŲØŊŲا اØģØŠŲاØŊŲ Ų
ÛâØīŲØŊ. ØĻÛØīØŠØą ØĒØēŲ
اÛØīâŲØ§Û Ų
ØŊØąØģŲâØ§Û Ø§ØšŲØĻ ØīاŲ
Ų ØŠØšÛÛØą ØŊŲ
ا Ų/Ûا ØšŲØļØŠ Ų
ŲاØŊ Ų
ŲØąØŊ اØģØŠŲاØŊŲ ØĻŲ Ų
ŲØļŲØą ŲØīاŲ ØŊاØŊŲ ØŠØĢØŦÛØąØ§ØŠ اÛŲ Ų
اØŊŲ ØĻØą ÚŊØąØ§ŲâØąŲÛ Ø§ØģØŠ. ØąŲØīâŲØ§Û ØĩŲØđØŠÛ ØīاŲ
Ų ØĻØģÛØ§ØąÛ Ø§Øē ØąŲØšŲâŲØ§Û Ų
ØŪØŠŲŲ Ų Ų
اÛØđا؊ ØĻØģŲūØ§ØąÛ Ų
اŲŲØŊ Ų
ØŲŲŲ Ųا Ų
ÛâØĻاØīØŊ.
اŲŲ
ÛØŠ ŲاŲŲŲ اØģØŠŲÚĐØģ ØĻا اÛŲ ŲاŲØđÛØŠ ŲØīاŲ ØŊاØŊŲ Ų
ÛâØīŲØŊ ÚĐŲ ŲŲØī Ų
ŲŲ
Û ØŊØą ØŠØŲÛŲØ§ØŠÛ ÚĐŲ Ų
ŲØŽØą ØĻŲ ØØŊاŲŲ ØģŲ ؎اÛØēŲ ŲŲØĻŲ ØīØŊØ Ø§ÛŲا ÚĐØąØŊ.
ŲاŲŲŲ اØģØŠŲÚĐØģ ØĻØąØ§Û ØŊØąÚĐ ØīŲØ§Û ØąÛØēاŲØŊاŲ
ÚŊاŲâŲا Ų ØēاŲ
ŲâŲا Ų
ŲŲ
اØģØŠ. ŲŲ
ÚŲÛŲØ ØąØģŲØĻâÚŊØ°Ø§ØąÛ Ø°ØąØ§ØŠ Ų Ų
ŲØŽŲØŊا؊ ÚĐŲÚÚĐ ØŊØą ØĒØĻØ ØŠØØŠ ŲÛØąŲÛ ÚŊØąØ§ŲØī.
ØŊØą ŲŲØ§Ø ŲŲ
ÛŲ ŲØļØąÛŲ ØąØ§ Ų
ÛâØŠŲاŲ ØĻØąØ§Û ØŠŲØķÛØ Ø§ÛŲÚĐŲ ÚØąØ§ ŲØ·ØąØ§ØŠ ÚĐŲÚÚĐ ØĒØĻ (Ûا ÚĐØąÛØģ؊اŲâŲØ§Û ÛØŪ) Ų
ÛâØŠŲاŲŲØŊ ØŊØą ŲŲا Ų
ØđŲŲ ØĻŲ
اŲŲØŊ (ØĻŲ ØĩŲØąØŠ اØĻØą) ؊ا ØēŲ
اŲÛ ÚĐŲ ØĻŲ اŲØŊاØēŲ ØĻØØąØ§ŲÛ ØąØīØŊ ÚĐŲŲØŊ Ų ØĻŲ ØĩŲØąØŠ ØĻØ§ØąØ§Ų (Ûا ØĻØąŲ Ų ØŠÚŊØąÚŊ) ØīØąŲØđ ØĻŲ ØąÛØēØī ÚĐŲŲØŊØ Ø§ØģØŠŲاØŊŲ ØīŲØŊ. [Ûģ] اØģØŠŲاØŊŲ Ų
ØīاØĻŲÛ Ø§Øē Ų
ØđاØŊŲŲ Ų
ÛâØŠŲاŲØŊ ØŊØą ØŠŲâŲØīÛŲ ØīØŊŲ Ø°ØąØ§ØŠ ØąÛØē ØŊØą ØĒØĻ Ûا ØīØ§ØąŲâŲØ§Û ØŊÛÚŊØą اŲ؎اŲ
ØīŲØŊ.
ØģØąØđØŠ ØØŊ ÚĐØąŲ ØŊØą ØاŲ ØģŲŲØ· ØŊØą ÛÚĐ ØīØ§ØąŲ
![]() ØŽØąÛاŲ ØŪØēŲØŊŲ اØē ÚĐŲØ§Øą ÛÚĐ ÚĐØąŲ ØŊØą ØاŲ ØģŲŲØ· ØŊØą ÛÚĐ ØīØ§ØąŲ (ØĻŲ ØđŲŲاŲ Ų
ØŦاŲØ ŲØ·ØąŲâØ§Û Ø§Øē Ų
Ų ÚĐŲ ØŊØą ŲŲا Ų
ÛâاŲØŠØŊ): ØŪØ·ŲØ· ØŽØąÛاŲ Ø ŲÛØąŲÛ ÚĐØīØī Fd Ų ŲÛØąŲÛ ÚŊØąØ§ŲØī Fg .
ØŽØąÛاŲ ØŪØēŲØŊŲ اØē ÚĐŲØ§Øą ÛÚĐ ÚĐØąŲ ØŊØą ØاŲ ØģŲŲØ· ØŊØą ÛÚĐ ØīØ§ØąŲ (ØĻŲ ØđŲŲاŲ Ų
ØŦاŲØ ŲØ·ØąŲâØ§Û Ø§Øē Ų
Ų ÚĐŲ ØŊØą ŲŲا Ų
ÛâاŲØŠØŊ): ØŪØ·ŲØ· ØŽØąÛاŲ Ø ŲÛØąŲÛ ÚĐØīØī Fd Ų ŲÛØąŲÛ ÚŊØąØ§ŲØī Fg .
ØŊØą ØģØąØđØŠ ØØŊ(Ûا ØŠŲâŲØīÛŲÛ) Ø ŲÛØąŲÛ Ø§ØķاŲÛ Fg ŲاØīÛ Ø§Øē ØŠŲاŲØŠ ØĻÛŲ ŲØēŲ Ų ØīŲاŲØąÛ ÚĐØąŲ (ŲØą ØŊŲ ŲاØīÛ Ø§Øē ÚŊØąØ§ŲØī [Ûī] ) ØĻŲ ŲØģÛŲŲ:

ÚĐŲ Ïp Ų Ïf ØĻŲ ØŠØąØŠÛØĻ ÚÚŊاŲÛ ÚĐØąŲ Ų ØīØ§ØąŲ Ų g Øī؊اØĻ ÚŊØąØ§ŲØīÛ. ŲÛاØē ØĻŲ ØŠØđاØŊŲ ŲÛØąŲ Fd = Fg Ų ØŲ ØģØąØđØŠ v ØģØąØđØŠ ØØŊ vs ØąØ§ ØĻŲ ØŊØģØŠ Ų
ÛâØĒŲØąØŊ. ØŠŲØŽŲ ØŊاØīØŠŲ ØĻاØīÛØŊ ÚĐŲ اØē ØĒŲ؎اÛÛ ÚĐŲ ŲÛØąŲÛ Ø§ØķاŲÛ ØĻا R3 اŲØēاÛØī Ų
ÛâÛاØĻØŊ Ų ÚĐØīØī اØģØŠŲÚĐØģ ØĻا R اŲØēاÛØī Ų
ÛâÛاØĻØŊØ ØģØąØđØŠ ØØŊ ØĻا R2 اŲØēاÛØī Ų
ÛâÛاØĻØŊ Ų ØĻŲاØĻØąØ§ÛŲ ØĻا اŲØŊاØēŲ Ø°ØąØ§ØŠ Ų
طاØĻŲ ØīÚĐŲ ØēÛØą ØĻØģÛØ§Øą ØŠØšÛÛØą Ų
ÛâÚĐŲØŊ. اÚŊØą ÛÚĐ Ø°ØąŲ ŲŲØ· ŲØēŲ ØŪŲØŊ ØąØ§ ØŊØą ØÛŲ ØģŲŲØ· ØŊØą ÛÚĐ ØīØ§ØąŲ ØŊØ§ØąØ§Û ÚŊØąØ§ŲâØąŲÛ ØŠØŽØąØĻŲ ÚĐŲØŊØ ØĒŲÚŊاŲ ØģØąØđØŠ ØØŊ ØēŲ
اŲÛ ØاØĩŲ Ų
Û ØīŲØŊ ÚĐŲ Ų
ØŽŲ
ŲØđ اØĩØ·ÚĐاÚĐ Ų ŲÛØąŲÛ ØīŲاŲØąÛ ØĻØą Ø°ØąŲ ŲاØīÛ Ø§Øē ØīØ§ØąŲ ØŊŲÛŲاŲ ØĻا ŲÛØąŲÛ ÚŊØąØ§ŲØī Ų
ØŠØđاØŊŲ ØīŲØŊ. اÛŲ ØģØąØđØŠ v (m/s) ØĻŲ ØĩŲØąØŠ ØēÛØą ØĻŲâØŊØģØŠ Ų
ÛâØĒÛØŊ: [Ûī]

(ØĻŲ ØĩŲØąØŠ ØđŲ
ŲØŊÛ ØĻŲ ØģŲ
ØŠ ŲūاÛÛŲ اÚŊØą ρ p > ρ f Ø ØĻŲ ØģŲ
ØŠ ØĻاŲا اÚŊØą ρ p < ρ f )Ø ØŽØ§ÛÛ ÚĐŲ:
- g Øī؊اØĻ ÚŊØąØ§ŲØīÛ Ø§ØģØŠ (m/s 2 )
- R ØīØđاØđ Ø°ØąŲ ÚĐØąŲÛ (m) اØģØŠ.
- ρ p ÚÚŊاŲÛ Ø°ØąŲ اØģØŠ (kg/ m3 ).
- ρ f ÚÚŊاŲÛ ØīØ§ØąŲ اØģØŠ (kg/ m3 )
- Ξ ÚŊØąØ§ŲâØąŲÛ ØŊÛŲاŲ
ÛÚĐÛ (kg/(m*s)) اØģØŠ.
اØģØŠØŪØąØ§ØŽ
ØŽØąÛاŲ ØŦاØĻØŠ اØģØŠŲÚĐØģ
ØŊØą ØŽØąÛاŲ اØģØŠŲÚĐØģØ ØŊØą ØđØŊØŊ ØąÛŲŲŲØŊØē ØĻØģÛØ§Øą ŲūاÛÛŲØ ØīØąØ§ÛØ· Øī؊اØĻ ŲŲ
ØąŲØŠÛ ØŊØą Ų
ØđاØŊŲا؊ ŲاŲÛŲ-اØģØŠŲÚĐØģ ŲاØŊÛØŊŲ ÚŊØąŲØŠŲ ØīØŊŲâاØģØŠ. ØģŲūØģ Ų
ØđاØŊŲا؊ ØŽØąÛاŲ ØĻØąØ§Û ÛÚĐ ØŽØąÛاŲ ØŦاØĻØŠ ØŠØąØ§ÚĐŲ
ŲاŲūØ°ÛØą ØŠØĻØŊÛŲ ØĻŲ ØĩŲØąØŠ ØēÛØą ŲŲ
اÛØī ØŊاØŊŲ Ų
ÛâØīŲŲØŊ: [Ûĩ]

؎اÛÛ ÚĐŲ:
- p ŲØīØ§Øą ØīØ§ØąŲ (ØĻØą ØØģØĻ Pa) اØģØŠ.
- u ØģØąØđØŠ ØŽØąÛاŲ (ØĻØą ØØģØĻ Ų
ØŠØą ØĻØą ØŦاŲÛŲ) Ų
- Ï ŲØąØŠÛØģÛØŠŲ اØģØŠ (ØŊØą s -1 )Ø ÚĐŲ ØĻŲ ØĩŲØąØŠ ØŠØđØąÛŲ ØīØŊŲ اØģØŠ

ØĻا اØģØŠŲاØŊŲ اØē ØĻØąØŪÛ Ø§Øē ŲÛÚÚŊÛâŲØ§Û ØĻØąØŊØ§Øą Ų
ØاØģØĻا؊ÛØ Ų
ÛâØŠŲاŲ ŲØīاŲâØŊاØŊ ÚĐŲ اÛŲ Ų
ØđاØŊŲا؊ ØĻŲ Ų
ØđاØŊŲا؊ ŲاŲūŲاØģ ØĻØąØ§Û ŲØīØ§Øą Ų ŲØą ÛÚĐ Ø§Øē Ų
ŲŲŲŲâŲØ§Û ØĻØąØŊØ§Øą ŲØąØŠÛØģÛØŠŲ Ų
ŲØŽØą Ų
Û ØīŲŲØŊ: [Ûĩ]
 and
and 
ŲÛØąŲŲØ§Û Ø§ØķاŲÛ Ų
اŲŲØŊ ŲÛØąŲŲØ§Û ÚŊØąØ§ŲØīÛ Ų ØīŲاŲØąÛ ØŊØą ŲØļØą ÚŊØąŲØŠŲ ŲØīØŊŲâاŲØŊØ Ø§Ų
ا ØĻŲ ØąØ§ØØŠÛ Ų
ÛâØŠŲاŲ ØĒŲâŲا ØąØ§ اØķاŲŲ ÚĐØąØŊ ØēÛØąØ§ Ų
ØđاØŊŲا؊ ŲŲŲØ ØŪØ·Û ŲØģØŠŲØŊØ ØĻŲاØĻØąØ§ÛŲ Ų
ÛâØŠŲاŲ ØĻØąŲŲ
âŲŲÛ ØŪØ·Û ØąØ§ŲâØŲâŲا Ų ŲÛØąŲŲØ§Û Ų
ØąØŠØĻØ· ØąØ§ اØđŲ
اŲ ÚĐØąØŊ.
ØŽØąÛاŲ ØđØąØķÛ ØŲŲ ÛÚĐ ÚĐØąŲ
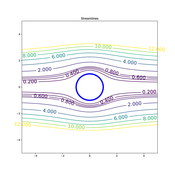 ØŪØ·ŲØ· ØŽØąÛاŲÛ ØŪØēŲØŊŲ اØē ÚĐŲØ§Øą ÛÚĐ ÚĐØąŲ ØŊØą ÛÚĐ ØīØ§ØąŲ Ų
ÛâÚŊØ°ØąØŊ.اÛØēŲÚĐاŲØŠŲØąŲØ§Û ØŠØ§ØĻØđ Ï (Ų
ŲاØŊÛØą ØŊØą ØĻØąÚØģØĻâŲØ§Û ÚĐاŲØŠŲØą).
ØŪØ·ŲØ· ØŽØąÛاŲÛ ØŪØēŲØŊŲ اØē ÚĐŲØ§Øą ÛÚĐ ÚĐØąŲ ØŊØą ÛÚĐ ØīØ§ØąŲ Ų
ÛâÚŊØ°ØąØŊ.اÛØēŲÚĐاŲØŠŲØąŲØ§Û ØŠØ§ØĻØđ Ï (Ų
ŲاØŊÛØą ØŊØą ØĻØąÚØģØĻâŲØ§Û ÚĐاŲØŠŲØą).
ØŊØą Ų
ŲØąØŊ ÛÚĐ ÚĐØąŲ ØŊØą ÛÚĐ ØŽØąÛاŲ Ų
ÛØŊاŲ ØŊŲØą ÛÚĐŲŲاØŪØŠØ Ø§ØģØŠŲاØŊŲ اØē ÛÚĐ ØŊØģØŠÚŊاŲ Ų
ØŪØŠØĩا؊ اØģØŠŲاŲŲâØ§Û ØģŲØŊŲ
ŲØŊ اØģØŠ ( r , Ï , z ). Ų
ØŲØą z اØē Ų
ØąÚĐØē ÚĐØąŲ ØđØĻŲØą Ų
ÛâÚĐŲØŊ Ų ØĻا ØŽŲØŠ ØŽØąÛاŲ Ų
ØŠŲØģØ· ŲŲ
âØŠØąØ§Øē اØģØŠØ ØŊØą ØاŲÛ ÚĐŲ r ØīØđاØđ ØđŲ
ŲØŊ ØĻØą Ų
ØŲØą z اØģØŠ. Ų
ØĻØŊØĢ ØŊØą Ų
ØąÚĐØē ÚĐØąŲ اØģØŠ. اØē ØĒŲ؎اÛÛ ÚĐŲ ØŽØąÛاŲ ØŲŲ Ų
ØŲØą z Ų
ØŠŲØ§ØąŲ اØģØŠØ Ų
ØģØŠŲŲ اØē ØĒØēÛŲ
ŲØŠ Ï Ø§ØģØŠ.
ØŊØą اÛŲ ØŊØģØŠÚŊاŲ Ų
ØŪØŠØĩا؊ اØģØŠŲاŲŲâاÛØ ØŽØąÛاŲ ØŠØąØ§ÚĐŲ
ŲاŲūØ°ÛØą ØąØ§ Ų
ÛâØŠŲاŲ ØĻا ؊اØĻØđ ØŽØąÛاŲ اØģØŠŲÚĐØģ Ï Ø ØĻØģØŠŲ ØĻŲ r Ų z ØŠŲØĩÛŲ ÚĐØąØŊ: [Ûķ] [Û·]

u r Ų u z ØĻŲ ØŠØąØŠÛØĻ Ų
ŲŲŲŲâŲØ§Û ØģØąØđØŠ ØŽØąÛاŲ ØŊØą ØŽŲØŠ r Ų z ŲØģØŠŲØŊ. Ų
ŲŲŲŲ ØģØąØđØŠ ØĒØēÛŲ
Ų؊اŲ ØŊØą اÛŲ Ų
ØŲØą Ų
ØŠŲØ§ØąŲØ ØŊØą ØŽŲØŠ Ï ØĻØąØ§ØĻØą ØĻا ØĩŲØą اØģØŠ. ØīØ§Øą ØØŽŲ
ÛØ Ø§Øē Ø·ØąÛŲ ŲŲŲŲâØ§Û ÚĐŲ ØĻا ØģØ·ØÛ ØĻا Ų
ŲØŊØ§Øą ØŦاØĻØŠ Ï Ų
ØØŊŲØŊ ØīØŊŲâاØģØŠØ ØĻØąØ§ØĻØą 2Ï Ï Ų ØŦاØĻØŠ اØģØŠ. [Ûķ]
ØĻØąØ§Û Ø§ÛŲ Ų
ŲØąØŊ اØē ÛÚĐ ØŽØąÛاŲ Ų
ØŠŲØ§ØąŲ Ų
ØŲØąÛØ ØŠŲŲا Ų
ØĪŲŲŲ ØšÛØą ØĩŲØą ØĻØąØŊØ§Øą ŲØąØŠÛØģÛØŠŲ ÏØ ØĒØēÛŲ
Ų؊اŲ Ï-Ų
ŲŲŲŲ ÏÏ Ø§ØģØŠ: [Ûļ] [Ûđ]

ØđŲ
ŲÚŊØą ŲاŲūŲاØģ ÚĐŲ ØĻØą ŲØąØŠÛØģÛØŠŲ ÏÏ Ø§ØđŲ
اŲ Ų
ÛâØīŲØŊØ ØŊØą اÛŲ ØŊØģØŠÚŊاŲ Ų
ØŪØŠØĩا؊ اØģØŠŲاŲŲâØ§Û ØĻا ØŠŲØ§ØąŲ Ų
ØŲØąÛ ØŠØĻØŊÛŲ Ų
ÛâØīŲØŊ: [Ûđ]

اØē ØŊŲ Ų
ØđاØŊŲŲ ŲØĻŲÛ Ų ØĻا ØīØąØ§ÛØ· Ų
ØąØēÛ Ų
ŲاØģØĻØ ØĻØąØ§Û ØģØąØđØŠ ØŽØąÛاŲ ÛÚĐŲŲاØŪØŠ Ų
ÛØŊاŲ ØŊŲØą u ØŊØą ØŽŲØŠ z Ų ÚĐØąŲâØ§Û ØĻŲ ØīØđاØđ R Ø ØŽŲاØĻ ØĻŲ ØŊØģØŠ Ų
Û ØĒÛØŊ: [ÛąÛ°]
![{\displaystyle \psi (r,z)=-{\frac {1}{2}}\,u\,r^{2}\,\left[1-{\frac {3}{2}}{\frac {R}{\sqrt {r^{2}+z^{2}}}}+{\frac {1}{2}}\left({\frac {R}{\sqrt {r^{2}+z^{2}}}}\right)^{3}\;\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/218591cdc853f0ae1258027cfbf24dc57bc830d6)
 اØģØŠŲÚĐØģ-ØŽØąÛاŲ ØŊØą Ø§Ø·ØąØ§Ų ÚĐØąŲ ØĻا ŲūØ§ØąØ§Ų
ØŠØąŲØ§Û ØģØąØđØŠ Ų
ÛØŊاŲ ØŊŲØą
اØģØŠŲÚĐØģ-ØŽØąÛاŲ ØŊØą Ø§Ø·ØąØ§Ų ÚĐØąŲ ØĻا ŲūØ§ØąØ§Ų
ØŠØąŲØ§Û ØģØąØđØŠ Ų
ÛØŊاŲ ØŊŲØą  Ø ØīØđاØđ ÚĐØąŲ
Ø ØīØđاØđ ÚĐØąŲ  ÚŊØąØ§ŲâØąŲÛ ØĒØĻ (T = 20 ØŊØąØŽŲ ØģاŲØŠÛâÚŊØąØ§ØŊ)
ÚŊØąØ§ŲâØąŲÛ ØĒØĻ (T = 20 ØŊØąØŽŲ ØģاŲØŠÛâÚŊØąØ§ØŊ)  . ØŪØ·ŲØ· Ų
ÛØŊاŲŲ Ų
ÛØŊاŲŲ ØģØąØđØŠ Ų ØŊاŲ
ŲŲâŲØ§Û ØģØąØđØŠØ ŲØīØ§Øą Ų ŲØąØŠÛØģÛØŠŲ ØĻا ØīØĻŲâØąŲÚŊâŲا ŲØīاŲ ØŊاØŊŲ ØīØŊŲâاØģØŠ.
. ØŪØ·ŲØ· Ų
ÛØŊاŲŲ Ų
ÛØŊاŲŲ ØģØąØđØŠ Ų ØŊاŲ
ŲŲâŲØ§Û ØģØąØđØŠØ ŲØīØ§Øą Ų ŲØąØŠÛØģÛØŠŲ ØĻا ØīØĻŲâØąŲÚŊâŲا ŲØīاŲ ØŊاØŊŲ ØīØŊŲâاØģØŠ.
ØąØ§ŲâØŲ ØģØąØđØŠ ØŊØą ØŊØģØŠÚŊاŲ Ų
ØŪØŠØĩا؊ اØģØŠŲاŲŲâØ§Û ØĻŲ ØĩŲØąØŠ ØēÛØą اØģØŠ:


ØŲ ŲØąØŠÛØģÛØŠŲ ØŊØą ØŊØģØŠÚŊاŲ Ų
ØŪØŠØĩا؊ اØģØŠŲاŲŲâØ§Û ØĻŲ ØĩŲØąØŠ ØēÛØą اØģØŠ:

ØąØ§ŲâØŲ ŲØīØ§Øą ØŊØą ØŊØģØŠÚŊاŲ Ų
ØŪØŠØĩا؊ اØģØŠŲاŲŲâØ§Û ØĻŲ ØĩŲØąØŠ ØēÛØą اØģØŠ:

ØąØ§ŲâØŲ ŲØīØ§Øą ØŊØą ØŊØģØŠÚŊاŲ Ų
ØŪØŠØĩا؊ ÚĐØąŲÛ ØĻŲ ØĩŲØąØŠ ØēÛØą اØģØŠ:

ŲØąŲ
ŲŲ ŲØīØ§Øą ŲŲ
ÚŲÛŲ Ųū؊اŲØģÛŲ ØŊŲŲØ·ØĻÛ Ų
ØīاØĻŲ Ų
ŲŲŲŲ
ØŊØą اŲÚĐØŠØąŲاØģ؊ا؊ÛÚĐ ŲاŲ
ÛØŊŲ Ų
Û ØīŲØŊ.
ÛÚĐ ŲØąŲ
ŲŲ ÚĐŲÛâØŠØąØ ØĻا ØĻØąØŊØ§Øą ØģØąØđØŠ Ų
ÛØŊاŲ ØŊŲØą ØŊŲØŪŲاŲ  Ø ØŊØą ØŊØģØŠÚŊاŲ Ų
ØŪØŠØĩا؊ ØŊÚĐØ§ØąØŠÛ
Ø ØŊØą ØŊØģØŠÚŊاŲ Ų
ØŪØŠØĩا؊ ØŊÚĐØ§ØąØŠÛ  ØĻŲ ØĩŲØąØŠ ØēÛØą ŲØīاŲ ØŊاØŊŲ Ų
ÛâØīŲØŊ:
ØĻŲ ØĩŲØąØŠ ØēÛØą ŲØīاŲ ØŊاØŊŲ Ų
ÛâØīŲØŊ:


ØŊØą اÛŲ ŲØąŲ
ŲŲØ Ø§ØĩØ·ŲØ§Ø ŲاŲūاÛØģØŠØ§Øą ŲŲØđÛ ØĻŲ اØĩØ·ŲØ§Ø Ø§ØģØŠŲÚĐØģŲØŠ ØąØ§ ŲØīاŲ Ų
ÛâØŊŲØŊ. اØģØŠÚĐŲØģŲŲØŠ ؊اØĻØđ ÚŊØąÛŲ اØē Ų
ØđاØŊŲا؊ اØģØŠŲÚĐØģ-ØŽØąÛاŲ اØģØŠ. ØđØĻØ§ØąØŠ ŲūاÛØģØŠØ§Øą ØĻØąØ§ØĻØą ØĻا Ų
ÛØŊاŲ ÚŊØąØ§ØŊÛاŲ ØŊŲŲØ·ØĻÛ Ø§ØģØŠ. ŲØąŲ
ŲŲ ŲØąØŠÛØģÛØŠŲ Ų
ØīاØĻŲ ŲاŲŲŲ ØĻÛŲ-ØģاŲØ§Øą ØŊØą اŲÚĐØŠØąŲŲ
ØšŲاطÛØģ اØģØŠ.
ŲØąŲ
ŲŲ ØēÛØą ؊اŲØģŲØą ØŠŲØī ØīØ§ØąŲ ØŊØ§ØąØ§Û ÚŊØąØ§ŲâØąŲÛ ØąØ§ ØĻØąØ§Û ØاŲØŠ ØŪاØĩ ØŽØąÛاŲ اØģØŠŲÚĐØģ ØŠŲØĩÛŲ Ų
ÛâÚĐŲØŊ ÚĐŲ ØŊØą Ų
ØاØģØĻŲ ŲÛØąŲÛ ŲØ§ØąØŊ ØĻØą Ø°ØąŲ Ų
ŲØąØŊ ŲÛاØē اØģØŠ. ØŊØą Ų
ØŪØŠØĩا؊ ØŊÚĐØ§ØąØŠÛ ØĻØąØŊØ§Øą- ÚŊØąØ§ØŊÛاŲ  ØĻا Ų
Ø§ØŠØąÛØģ ÚاÚĐŲØĻÛ ÛÚĐØģاŲ اØģØŠ. Ų
Ø§ØŠØąÛØģ
ØĻا Ų
Ø§ØŠØąÛØģ ÚاÚĐŲØĻÛ ÛÚĐØģاŲ اØģØŠ. Ų
Ø§ØŠØąÛØģ  ŲØīاŲ ØŊŲŲØŊŲ Ų
Ø§ØŠØąÛØģ ŲÛÚÚŊÛ Ø§ØģØŠ .
ŲØīاŲ ØŊŲŲØŊŲ Ų
Ø§ØŠØąÛØģ ŲÛÚÚŊÛ Ø§ØģØŠ .

ŲÛØąŲÛ ŲØ§ØąØŊ ØĻØą ÚĐØąŲ ØĻا اŲØŠÚŊØąØ§Ų ØģØ·Ø Ų
ØاØģØĻŲ Ų
ÛâØīŲØŊØ ØŽØ§ÛÛ ÚĐŲ  ŲاØØŊ ØĻØąØŊØ§Øą ØīØđاØđÛ ØŊØģØŠÚŊاŲ Ų
ØŪØŠØĩا؊ ÚĐØąŲÛ ØąØ§ ŲØīاŲ Ų
ÛâØŊŲØŊ:
ŲاØØŊ ØĻØąØŊØ§Øą ØīØđاØđÛ ØŊØģØŠÚŊاŲ Ų
ØŪØŠØĩا؊ ÚĐØąŲÛ ØąØ§ ŲØīاŲ Ų
ÛâØŊŲØŊ:

ØŽØąÛاŲ ÚØąØŪØīÛ ØŲŲ ÛÚĐ ÚĐØąŲ
 اØģØŠŲÚĐØģ - ØŽØąÛاŲ ØŊØą Ø§Ø·ØąØ§Ų ÚĐØąŲ:
اØģØŠŲÚĐØģ - ØŽØąÛاŲ ØŊØą Ø§Ø·ØąØ§Ų ÚĐØąŲ:  Ø
Ø  Ø
Ø 





اŲŲاØđ ØŊÛÚŊØą ØŽØąÛاŲ اØģØŠŲÚĐØģ
اÚŊØąÚŲ Ų
اÛØđ ØģاÚĐŲ اØģØŠ Ų ÚĐØąŲ ØĻا ØģØąØđØŠ Ų
ØđÛŲÛ ØŊØą ØاŲ ØØąÚĐØŠ اØģØŠØ ØĻا ØŠŲØŽŲ ØĻŲ ØģاØŪØŠØ§Øą ÚĐØąŲØ ÚĐØąŲ ØŊØą ØاŲØŠ ØģÚĐŲŲ ØŊØą ŲØļØą ÚŊØąŲØŠŲ Ų
ÛâØīŲØŊ Ų Ų
اÛØđ ØąØ§ ØŊØą ØاŲØŠ ØŽØąÛاŲØ ØŊØą ØŽŲØŠ Ų
ØŪاŲŲ ØØąÚĐØŠ ÚĐØąŲ ØŊØą ŲØļØą ÚŊØąŲØŠŲ Ų
ÛâØīŲØŊ.
ŲŲ
ÚŲÛŲ ØĻØĻÛŲÛØŊ
Ų
ŲاØĻØđ
- â Stokes, G. G. (1851). "On the effect of internal friction of fluids on the motion of pendulums". Transactions of the Cambridge Philosophical Society. 9, part ii: 8â106. Bibcode:1851TCaPS...9....8S.
The formula for terminal velocity (V) appears on p. [52], equation (127).
- â Batchelor (1967), p. 233.
- â Hadley, Peter. "Why don't clouds fall?". Institute of Solid State Physics, TU Graz. Archived from the original on 12 June 2017. Retrieved 30 May 2015.
- â ÛīŲŦÛ° ÛīŲŦÛą Lamb (1994), §337, p. 599.
- â ÛĩŲŦÛ° ÛĩŲŦÛą Batchelor (1967), section 4.9, p. 229.
- â ÛķŲŦÛ° ÛķŲŦÛą Batchelor (1967), section 2.2, p. 78.
- â Lamb (1994), §94, p. 126.
- â Batchelor (1967), section 4.9, p. 230
- â ÛđŲŦÛ° ÛđŲŦÛą Batchelor (1967), appendix 2, p. 602.
- â Lamb (1994), §337, p. 598.