|
ž»ž▒┌»ž¦┘ć ž▒█īž¦žČ█īž¦ž¬
 ┘å┘ģž¦ž» ž▒█īž¦žČ█ī ┘å┘ģž¦ž» ž▒█īž¦žČ█ī
ž▒█īž¦žČ█īž¦ž¬ (Mathematics) ž▒ž¦ ┘ģž╣┘ģ┘ł┘䞦┘ŗ ž»ž¦┘åž┤ ž©ž▒ž▒ž│█ī ┌®┘ģ█īž¬ŌĆī┘枦 ┘ł ž│ž¦ž«ž¬ž¦ž▒ŌĆī┘枦 ┘ł ┘üžČž¦ ┘ł ž¬ž©ž»█ī┘ä ž¬ž╣ž▒█ī┘ü ┘ģ█īŌĆī┌®┘å┘åž». ž»█īž»┌»ž¦┘ć ž»█ī┌»ž▒█ī ž▒█īž¦žČ█ī ž▒ž¦ ž»ž¦┘åž┤█ī ┘ģ█īŌĆīž»ž¦┘åž» ┌®┘ć ž»ž▒ žó┘å ž©ž¦ ž¦ž│ž¬ž»┘䞦┘ä ┘ģ┘åžĘ┘é█ī ž¦ž▓ ž¦žĄ┘ł┘ä ┘ł ž¬ž╣ž▒█ī┘üŌĆī┘枦 ž©┘ć ┘垬ž¦█īž¼ ž»┘é█ī┘é ┘ł ž¼ž»█īž»█ī ┘ģ█īŌĆīž▒ž│█ī┘ģ. ž»█īž»┌»ž¦┘ćŌĆī┘枦█ī ž»█ī┌»ž▒█ī ┘å█īž▓ ž»ž▒ ┘ü┘äž│┘ü┘ć ž▒█īž¦žČ█īž¦ž¬ ž©█īž¦┘å ž┤ž»┘ćŌĆīž¦ž│ž¬.
ž¦┌»ž▒┌å┘ć ž▒█īž¦žČ█īž¦ž¬ ž«┘łž» █ī┌®█ī ž¦ž▓ ž╣┘ä┘ł┘ģ žĘž©█īž╣█ī ž©┘ćŌĆīž┤┘ģž¦ž▒ ┘å┘ģ█īŌĆīž▒┘łž» ┘ł┘ä█ī ž│ž¦ž«ž¬ž¦ž▒┘枦█ī ┘ł█ī┌ś┘ćŌĆīž¦█ī ┌®┘ć ž▒█īž¦žČ█īŌĆīž»ž¦┘垦┘å ┘ģ█īŌĆī┘Š┌ś┘ł┘ć┘åž»žī ž©█īž┤ž¬ž▒ ž¦ž▓ ž»ž¦┘åž┤ŌĆī┘枦█ī žĘž©█īž╣█ī ž©┘ć ┘ł█ī┌ś┘ć ┘ü█īž▓█ī┌® ž│ž▒┌åž┤┘ģ┘ć ┘ģ█īŌĆī┌»█īž▒┘åž» ┘ł ž»ž▒ ┘üžČž¦█ī█ī ž¼ž»ž¦ ž¦ž▓ žĘž©█īž╣ž¬ ┘ł ┘ģžŁžČŌĆī┌»┘ł┘å┘ć ┌»ž│ž¬ž▒ž┤ ┘Š█īž»ž¦ ┘ģ█īŌĆī┌®┘åž» ž©┘ć žĘ┘łž▒█ī ┌®┘ć ž╣┘ä┘ł┘ģ žĘž©█īž╣█ī ž©ž▒ž¦█ī žŁ┘ä ┘ģž│ž¦ž”┘ä ž«┘łž» ž©┘ć ž▒█īž¦žČ█ī ž©ž¦ž▓ ┘ģ█īŌĆī┌»ž▒ž»┘åž» ž¬ž¦ ž¼┘łž¦ž©ž┤ž¦┘å ž▒ž¦ ž©ž¦ žó┘å ┘ģ┘鞦█īž│┘ć ┘ł ž©ž▒ž▒ž│█ī ┌®┘å┘åž».
ž╣┘ä┘ł┘ģ žĘž©█īž╣█īžī ┘ģ┘ć┘åž»ž│█ī ┘ł ž¦┘鞬žĄž¦ž»žī ž©ž│█īž¦ž▒ ž©┘ć ž▒█īž¦žČ█īž¦ž¬ ž¬┌®█ī┘ć ž»ž¦ž▒┘åž». žó┘å ž©ž«ž┤ ž¦ž▓ ž▒█īž¦žČ█īž¦ž¬ ž▒ž¦ ┌®┘ć ž╣┘ä┘ł┘ģ ┌®ž¦ž▒ž©ž▒ž»█ī ž©┘ć žó┘å ž©█īž┤ž¬ž▒ ┘ģ█īŌĆī┘Šž▒ž»ž¦ž▓┘åž»žī ž▒█īž¦žČ█īž¦ž¬ ┌®ž¦ž▒ž©ž▒ž»█ī ┘ģ█īŌĆī┘垦┘ģ┘åž». ┘ł┘ä█ī ┌»ž¦┘ć ž▒█īž¦žČ█īŌĆīž»ž¦┘垦┘å ž©┘ć ž»┘䞦█ī┘ä žĄž▒┘üž¦┘ŗ ž▒█īž¦žČ█ī ┘ł ┘å┘ć ┌®ž¦ž▒ž©ž▒ž»█ī ž©┘ć ž¬ž╣ž▒█ī┘ü ┘ł ž©ž▒ž▒ž│█ī ž©ž▒ž«█ī ž│ž¦ž«ž¬ž¦ž▒┘枦 ┘ģ█īŌĆī┘Šž▒ž»ž¦ž▓┘åž» ┌®┘ć ž©┘ć žó┘å ž▒█īž¦žČ█īž¦ž¬ ┘ģžŁžČ ┌»┘üž¬┘ć ┘ģ█īŌĆīž┤┘łž».
┘å┘łž┤ž¬ž¦ž▒ ž©ž▒┌»ž▓█īž»┘ć
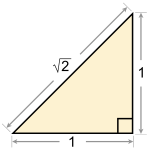
┘ć┘åž»ž│┘ć ┘ģžĘž¦┘äž╣┘ć┘ö ž¦┘å┘łž¦ž╣ ž▒┘łž¦ž©žĘ žĘ┘ł┘ä█ī ┘ł ž¦ž┤┌®ž¦┘ä ┘ł ž«žĄ┘łžĄ█īž¦ž¬ žó┘åŌĆī┘枦 ž¦ž│ž¬. ž¦█ī┘å ž»ž¦┘åž┤ ┘ć┘ģž▒ž¦┘ć ž©ž¦ žŁž│ž¦ž© █ī┌®█ī ž¦ž▓ ž»┘ł ž┤ž¦ž«┘ć┘ö ┘éž»█ī┘ģ█ī ž▒█īž¦žČ█īž¦ž¬ ž¦ž│ž¬. ┘łž¦┌ś┘ć┘ö ┘ć┘åž»ž│┘ćžī ž╣ž▒ž©█ī ž┤ž»┘ć┘ö ┘łž¦┌ś┘ć┘ö ┬½ž¦┘åž»ž¦ž▓┘ć┬╗ ž»ž▒ ┘üž¦ž▒ž│█ī ž¦ž│ž¬. ž»ž▒ ž▓ž©ž¦┘å ž¦┘å┌»┘ä█īž│█ī ž©┘ć žó┘å geometry ┘ł ž»ž▒ ž▓ž©ž¦┘å ┘üž▒ž¦┘åž│┘ć ž©┘ć žó┘å g├®om├®trie ┘ģ█īŌĆī┌»┘ł█ī┘åž» ┌®┘ć ┘ćž▒ ž»┘ł ž¦ž▓ ╬│╬ĄŽē╬╝╬ĄŽäŽü╬»╬▒ (┌»ž”┘ł┘ģž¬ž▒█īž¦) ž»ž▒ ž▓ž©ž¦┘å █ī┘ł┘垦┘å█ī žó┘ģž»┘ć ┌®┘ć ž©┘ć ┘ģž╣┘垦█ī ž¦┘åž»ž¦ž▓┘ćŌĆī┌»█īž▒█ī ž▓┘ģ█ī┘å ž¦ž│ž¬.
ž¦žŁž¬┘ģž¦┘䞦┘ŗ ž©ž¦ž©┘ä█īž¦┘å ┘ł ┘ģžĄž▒█īž¦┘å ┌®┘ć┘å ┘åž«ž│ž¬█ī┘å ┌®ž│ž¦┘å█ī ž©┘łž»┘åž» ┌®┘ć ž¦žĄ┘ł┘ä ┘ć┘åž»ž│┘ć ž▒ž¦ ┌®ž┤┘ü ┌®ž▒ž»┘åž». ┘ģžĄž▒█īž¦┘å ž▒┘łž┤ ž╣┘䞦┘ģž¬ŌĆī┌»ž░ž¦ž▒█ī ž▓┘ģ█ī┘åŌĆī┘枦 ž©ž¦ ž¬█īž▒┌® ┘ł žĘ┘垦ž© ž▒ž¦ ž¦ž©ž»ž¦ž╣ ┌®ž▒ž»┘åž». ž»ž▒ žóž║ž¦ž▓ ┘ć┘åž»ž│┘ć ž©ž▒ ┘Šž¦█ī┘ć┘ö ž»ž¦┘åž│ž¬┘ćŌĆī┘枦█ī ž¬ž¼ž▒ž©█ī ┘Šž▒ž¦┌®┘åž»┘ćŌĆīž¦█ī ž»ž▒ ┘ģ┘łž▒ž» žĘ┘ł┘ä ┘ł ž▓ž¦┘ł█ī┘ć ┘ł ┘ģž│ž¦žŁž¬ ┘ł žŁž¼┘ģ ┘éž▒ž¦ž▒ ž»ž¦ž┤ž¬ ┌®┘ć ž©ž▒ž¦█ī ┘ģž│ž¦žŁ█ī ┘ł ž│ž¦ž«ž¬┘ģž¦┘å ┘ł ┘åž¼┘ł┘ģ ┘ł ž©ž▒ž«█ī žĄ┘垦█īž╣ ž»ž│ž¬█ī ┘䞦ž▓┘ģ ┘ģ█īŌĆīž┤ž». ž©ž╣žČ█ī ž¦ž▓ ž¦█ī┘å ž»ž¦┘åž│ž¬┘ćŌĆī┘枦 ž©ž│█īž¦ž▒ ┘Š█īž┤ž▒┘üž¬┘ć ž©┘łž»┘åž» ┘ģž½┘䞦┘ŗ ┘ć┘ģ ┘ģžĄž▒█īž¦┘å ┘ł ┘ć┘ģ ž©ž¦ž©┘ä█īž¦┘å ┘éžČ█ī┘ć ┘ü█īž½ž¦ž║┘łž▒ž½ ž▒ž¦ █▒█Ą█░█░ ž│ž¦┘ä ┘éž©┘ä ž¦ž▓ ┘ü█īž½ž¦ž║┘łž▒ž½ ┘ģ█īŌĆīž┤┘垦ž«ž¬┘åž».
ž▓┘åž»┌»█īŌĆī┘垦┘ģ┘ć┘ö ž©ž▒┌»ž▓█īž»┘ć
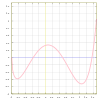 ┘å┘ģ┘łž»ž¦ž▒ ž¬ž¦ž©ž╣ ┘å┘ģ┘łž»ž¦ž▒ ž¬ž¦ž©ž╣
![{\displaystyle {\begin{aligned}&\scriptstyle f\colon [-1,1.5]\to [-1,1.5]\\&\textstyle x\mapsto {\frac {(4x^{3}-6x^{2}+1){\sqrt {x+1}}}{3-x}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/367545798d4c1d7748410deb9d03ea9faf400d6d)
ž¬ž¦ž©ž╣ █ī┌®█ī ž¦ž▓ ┘ģ┘üž¦┘ć█ī┘ģ ┘åžĖž▒█ī┘ć ┘ģž¼┘ģ┘łž╣┘ćŌĆī┘枦 ┘ł žŁž│ž¦ž© ž»█ī┘üž▒ž¦┘åž│█ī┘ä ┘ł ž¦┘垬┌»ž▒ž¦┘ä ž¦ž│ž¬. ž©žĘ┘łž▒ ž│ž¦ž»┘ć ┘ģ█īŌĆīž¬┘łž¦┘å ┌»┘üž¬ ┌®┘ć ž©┘ć ┘鞦ž╣ž»┘ćŌĆī┘枦█ī ž¬┘垦žĖž▒█ī ┌®┘ć ž©┘ć ┘ćž▒ ┘łž▒┘łž»█ī ž«┘łž» █ī┌® ┘ł ┘ü┘éžĘ █ī┌® ž«ž▒┘łž¼█ī ┘åž│ž©ž¬ ┘ģ█īŌĆīž»┘ć┘åž»žī ž¬ž¦ž©ž╣ ┌»┘üž¬┘ć ┘ģ█īŌĆīž┤┘łž».
ž¬ž¦ž©ž╣ ž©┘ć ž╣┘å┘łž¦┘å ┘ģ┘ü┘ć┘ł┘ģ█ī ž»ž▒ ž▒█īž¦žČ█īž¦ž¬žī ž¬┘łž│žĘ ┌»┘łž¬┘üž▒█īž» ┘䞦█īž©┘å█īž¬ž│ ž»ž▒ ž│ž¦┘ä █▒█Č█╣█┤žī ž©ž¦ ┘ćž»┘ü ž¬┘łžĄ█ī┘ü █ī┌® ┌®┘ģ█īž¬ ž»ž▒ ž▒ž¦ž©žĘ┘ć ž©ž¦ █ī┌® ┘ģ┘åžŁ┘å█ī ┘ģž¦┘å┘åž» ž┤█īž© █ī┌® ┘å┘ģ┘łž»ž¦ž▒ ž»ž▒ █ī┌® ┘å┘éžĘ┘ć ž«ž¦žĄ ž©┘ć ┘łž¼┘łž» žó┘ģž». ž¦┘ģž▒┘łž▓┘ć ž©┘ć ž¬┘łž¦ž©ž╣█ī ┌®┘ć ž¬┘łž│žĘ ┘䞦█īž©┘å█īž▓ ž¬ž╣ž▒█ī┘ü ž┤ž»┘åž»žī ž¬┘łž¦ž©ž╣ ┘ģž┤ž¬┘éŌĆī┘Šž░█īž▒ ┘ģ█īŌĆī┌»┘ł█ī█ī┘ģ.
┘å┘łž┤ž¬ž¦ž▒┘枦█ī ž©ž▒┌»ž▓█īž»┘ć
┘å┌»ž¦ž▒┘ć┘ö ž©ž▒┌»ž▓█īž»┘ć

┘ģ┘ÅžŁ█īžĘ ┘Ŗž¦ ┘Š┘Ŗž▒ž¦┘ģ┘ł┘å ž»ž▒ ┘ć┘åž»ž│┘ć ž©┘ć ž«žĘ ┘ł ┘ģž│█īž▒█ī ┘ģ█īŌĆī┌»┘ł█ī┘åž» ┌®┘ć █ī┌® ž│žĘžŁ ž▒ž¦ ž»ž▒ ┘ģ█īž¦┘å ž«┘łž» ┘ģ█īŌĆī┌»█īž▒ž». ┘ģžŁ█īžĘ ž©┘ć ┘ģž╣┘垦█ī ┘üž▒ž¦┌»█īž▒┘åž»┘ć ž¦ž│ž¬ ┘ł ž©┘ć ž»ž▒ž¦ž▓ž¦█ī ž©ž«ž┤ ž©█īž▒┘ł┘å█ī █ī┌® ž┤┌®┘ä ┌»┘üž¬┘ć ┘ģ█īŌĆīž┤┘łž». █īž╣┘å█ī ┘üž¦žĄ┘ä┘ćŌĆīž¦█ī ┌®┘ć ž©ž▒ ┘äž©┘ć ž©█īž▒┘ł┘å█ī █ī┌® ž┤┌®┘ä ┘ģ█īŌĆī┘Š█ī┘ģž¦█ī█ī┘ģ ž¬ž¦ ž©┘ć ┘å┘éžĘ┘ć ž¦┘ł┘ä ž«┘łž» ž©ž¦ž▓┌»ž▒ž»█ī┘ģ ┘ģžŁ█īžĘ ┘ģ█īŌĆī┌»┘ł█ī█ī┘ģ. ž©┘ć ž«┘łž» ┘äž©┘ć ž©█īž▒┘ł┘å█ī ┘å█īž▓ ž¦žĄžĘ┘䞦žŁž¦┘ŗ ┘ģžŁ█īžĘ ┌»┘üž¬┘ć ┘ģ█īŌĆīž┤┘łž».
┬½┘ģžĘž¦┘äž╣┘ć ž▒█īž¦žČ█ī ž©ž▒ž¦█ī┘ģ ž»┘ł ┘ģž▒žŁ┘ä┘ć ž»ž¦ž▒ž». ┘ģž▒žŁ┘ä█Ć ž¦┘ł┘ä ┘ģžĘž¦┘äž╣█Ć ┘Š┌ś┘ł┘ćž┤ŌĆī┘枦█ī ┘éž©┘ä█ī ž¦ž│ž¬. ž«┘łž¦┘åž»┘å ž▒█īž¦žČ█īž¦ž¬ ž▓█īž©ž¦žī ┘ģž½┘ä ┘éž»┘ģ ž▓ž»┘å ž»ž▒ █ī┌® ž┤┘ćž▒ ž¬ž¦ž▒█īž«█ī ž▓█īž©ž¦ ž¦ž│ž¬žī ┌®┘ć žĘ█ī žó┘å ž┤┘ģž¦ ž©┘垦┘枦█ī ž▓█īž©ž¦█ī█ī ┘ģ█īŌĆīž©█ī┘å█īž». ┘ģž▒žŁ┘ä┘ć ž»┘ł┘ģ ┘ģž½┘ä ž¦█ī┘å ž¦ž│ž¬ ┌®┘ć ┘垦┌»┘枦┘å ž©ž¦┘ä ž»ž▒žó┘łž▒ž»┘ģ ┘ł ┘ģ█īŌĆīž¬┘łž¦┘å┘ģ ž©ž▒ ┘üž▒ž¦ž▓ ž┤┘ćž▒ ┘Šž▒┘łž¦ž▓ ┌®┘å┘ģ ┘ł ┌å█īž▓┘枦█ī█ī ž▒ž¦ ž©ž©█ī┘å┘ģ ┌®┘ć ž¦ž▓ ž▒┘ł█ī ž▓┘ģ█ī┘å ┘ģž╣┘ä┘ł┘ģ ┘åž©┘łž»┬╗..
ŌĆö ┌®┘ł┌åž▒ ž©█īž▒┌®ž¦ž▒
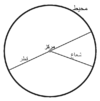 █ī┌® ž»ž¦█īž▒┘ć ž©ž¦ ┘ģž┤ž«žĄž¦ž¬ žó┘å (┘ģž▒┌®ž▓žī ž┤ž╣ž¦ž╣) █ī┌® ž»ž¦█īž▒┘ć ž©ž¦ ┘ģž┤ž«žĄž¦ž¬ žó┘å (┘ģž▒┌®ž▓žī ž┤ž╣ž¦ž╣)
ž»ž¦█īž▒┘ć ┘ģ┌®ž¦┘å ┘ć┘åž»ž│█ī ┘å┘鞦žĘ█ī ž¦ž▓ žĄ┘üžŁ┘ć ž¦ž│ž¬ ┌®┘ć ┘üž¦žĄ┘ä┘ćŌĆīž┤ž¦┘å ž¦ž▓ ┘å┘éžĘ┘ć┘ö ž½ž¦ž©ž¬█ī ┘łž¦┘éž╣ ž»ž▒ žó┘å žĄ┘üžŁ┘ćžī ┘ģ┘éž»ž¦ž▒ ž½ž¦ž©ž¬█ī ž©ž¦ž┤ž». ┘å┘éžĘ┘ć┘ö ž½ž¦ž©ž¬žī ┬½┘ģž▒┌®ž▓ ž»ž¦█īž▒┘ć┬╗žī ┘ł ┘ģ┘éž»ž¦ž▒ ž½ž¦ž©ž¬žī ┬½ž¦┘åž»ž¦ž▓┘ć┘ö ž┤ž╣ž¦ž╣ ž»ž¦█īž▒┘ć┬╗ ┘垦┘ģ█īž»┘ć ┘ģ█īŌĆīž┤┘łž».
ž»ž▒ žŁ┘é█ī┘鞬žī ž»ž¦█īž▒┘ć █ī┌® ž©█īžČ█ī ž¦ž│ž¬ ┌®┘ć ┌®ž¦┘å┘ł┘åŌĆī┘枦█ī žó┘å ž©ž▒ ┘ć┘ģž»█ī┌»ž▒ ┘ģ┘åžĘž©┘éŌĆīž¦┘åž».
 = ┘ģžŁ█īžĘ ž»ž¦█īž▒┘ć = ┘ģžŁ█īžĘ ž»ž¦█īž▒┘ć = ┘ģž│ž¦žŁž¬ ž»ž¦█īž▒┘ć = ┘ģž│ž¦žŁž¬ ž»ž¦█īž▒┘ć
žó█īž¦ ┘ģ█īŌĆīž»ž¦┘åž│ž¬█īž»ž¤
 žó█īž¦ ┘ģ█īŌĆīž»ž¦┘åž│ž¬█īž»... žó█īž¦ ┘ģ█īŌĆīž»ž¦┘åž│ž¬█īž»...
... ┌®┘ć ž¦ž╣ž»ž¦ž» ┌®ž¦ž¬ž¦┘䞦┘å ž©ž▒ž«█ī ž¦ž▓ ┘ģž│ž¦ž”┘ä ž¬ž▒┌®█īž©█īž¦ž¬█ī ┘ģž½┘ä žĘž▒┘é ž¬┌®┘ģ█ī┘ä ┘Šž▒ž¦┘垬ž▓ ┌»ž░ž¦ž▒█ī █ī┌® ž╣ž©ž¦ž▒ž¬ ž¼ž©ž▒█ī ž©ž¦  ž╣ž¦┘ģ┘ä ž▒ž¦ žŁ┘ä ┘ģ█ī ┌®┘åž»ž¤ ž╣ž¦┘ģ┘ä ž▒ž¦ žŁ┘ä ┘ģ█ī ┌®┘åž»ž¤
ž»ž▒┌»ž¦┘ćŌĆī┘枦█ī ┘łž¦ž©ž│ž¬┘ć
ž»ž▒ ž»█ī┌»ž▒ ┘Šž▒┘ł┌ś┘ćŌĆī┘枦█ī ┘ł█ī┌®█īŌĆī┘ģž»█īž¦
|