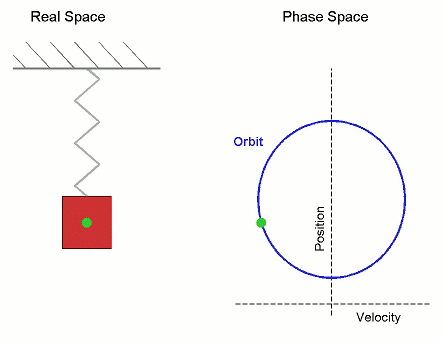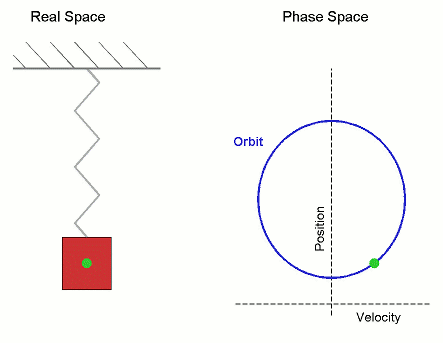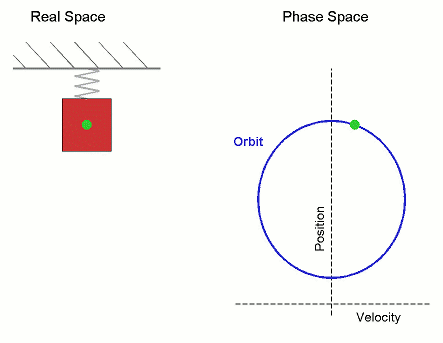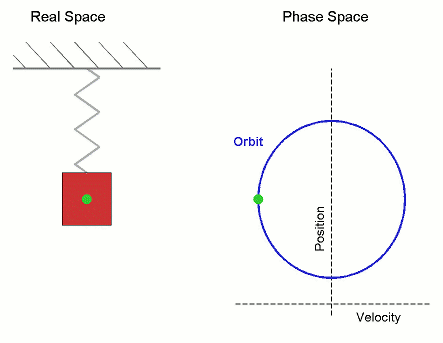
Órbita (dinámica)
|
Read other articles:

Ninth-century Muslim fortification in Mérida, Spain See also: Alcazaba (disambiguation) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Alcazaba of Mérida – news · newspapers · books · scholar · JSTOR (April 2023) (Learn how and when to remove this template message) Alcazaba of MéridaAlcazaba de MéridaLo...

Marquesado de Melgarejo Primer titular Juan Francisco Melgarejo y Zuazo-QuirogaConcesión Carlos VII de Nápoles3 de mayo de 1736Actual titular Caducado[editar datos en Wikidata] El marquesado de Melgarejo es un título nobiliario de Nápoles, después de las Dos Sicilias, concedido el 3 de mayo de 1736 por el rey Carlos VII de Nápoles, a Juan Francisco Melgarejo y Zuazo-Quiroga. Marqueses de Melgarejo Juan Francisco Melgarejo y Zuazo (Granada, 3 de julio de 1701-), I marqués de M...

British television game show (1977–1995, 2009–2010) The Krypton FactorThe Krypton Factor logo from 2009 until 2010GenreGame showCreated byJeremy FoxPresented byGordon Burns (1977–1995)Penny Smith (1995)Ross King (Young Krypton)Ben Shephard (2009–2010)Voices ofCharles Foster (uncredited)Country of originUnited KingdomOriginal languageEnglishNo. of series18 (Original)2 (Revival)2 (Young Krypton)No. of episodes254 (inc. 21 specials) (Original)20 (Revival)21 (Young Krypton)ProductionProdu...

TROS Tipo Empresa públicaIndustria Medios de comunicaciónForma legal asociaciónFundación 17 de diciembre de 1964Disolución 7 de septiembre de 2014Sede central Ámsterdam, Países BajosPresidente Ed NijpelsProductos Radio, Televisión, InternetPropietario Nederlandse Publieke OmroepSitio web http://www.tros.nl/[editar datos en Wikidata] Omroepvereniging TROS fue una organización pública de radio y televisión de los Países Bajos, que formó parte de la radiodifusi�...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: P. K. Roy Memorial College – news · newspapers · books · scholar · JSTOR (September 2022) (Learn how and when to remove this template message) P. K. Roy Memorial CollegeTypeUndergraduate collegeEstablished1960PrincipalKavita singhAddressP.K. Roy Memorial College, Main Road Saraidhela , Dhanbad, Jharkhand, ...

The Doll 2Poster FilmSutradara Rocky Soraya Produser Mohan Nankani Raam Soraya Rocky Soraya Ditulis oleh Riheam Junianti Rocky Soraya Fajar Umbara PemeranHerjunot AliLuna MayaSara WijayantoMaria SabtaRydhen AfexiIra Ilva SariMega CarefansaShofia ShireenWati SudiyonoPrincess MartinezPenata musikAnto HoedSinematograferAsep KalilaPenyuntingSastha SunuPerusahaanproduksiHitmaker StudiosTanggal rilis20 Juli 2017Durasi117 menitNegara IndonesiaBahasa Indonesia PendapatankotorRp 45,1 miliar...

Тетраморф у християнській інтерпретації як символ євангелістів, XIII століття, Кельн, слонова кістка, Музей Клюні (Франція) Видіння пророка Єзекіїля (Рафаель, 1518) Тетраморф (грец. τετραμορφος — чотиривидний) — в юдео-християнському віровченні та богослов'ї — крила�...

Laiz Laiz (Frankreich) Staat Frankreich Region Auvergne-Rhône-Alpes Département (Nr.) Ain (01) Arrondissement Bourg-en-Bresse Kanton Vonnas Gemeindeverband Veyle Koordinaten 46° 15′ N, 4° 53′ O46.2488888888894.8891666666667Koordinaten: 46° 15′ N, 4° 53′ O Höhe 173–210 m Fläche 10,31 km² Einwohner 1.306 (1. Januar 2020) Bevölkerungsdichte 127 Einw./km² Postleitzahl 01290 INSEE-Code 01203 Website https://laiz.fr/ Rathau...

Comunicação Tipos Social Massa Interpessoal Intrapessoal Verbal Não verbal Visual Audiovisual Segmentada Redes Ciberespacial Não violenta Meios Cartaz Cinema Correio Fanzine Internet Jornal Livro Outdoor Panfleto Podcast Banda desenhada Rádio Revista Televisão Vídeo Profissões Assessoria Design gráfico Editoração Jornalismo Produção audiovisual Produção cultural Produção editorial Publicidade Radialismo Relações públicas Roteiro Disciplinas Análise do discurso Análise de...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مايو 2022) كتاب مسألة المبيدات الحشرية: البيئة, الإقتصاد و الأخلاقيات هو كتاب نُشر عام 1993 من تأليف ديفيد بيمنتل وهيو ليمان. مسألة المبيدات الحشرية: البيئة, الإقتصاد , الأ�...

Светлана Степановна Самуляк Личная информация Пол женский Страна Украина Специализация тяжёлая атлетика Дата рождения 19 июля 2003(2003-07-19)[1] (20 лет) Награды и медали Чемпионаты мира Бронза Ташкент 2021 до 55 кг Чемпионаты Европы Серебро Ереван 2023 до 55 кг Государственные...

Le Clavier bien tempéré II Pour un article plus général, voir Le Clavier bien tempéré. Prélude et fugue n°17BWV 886Le Clavier bien tempéré, livre II (d) La bémol majeur Prélude Métrique / Fugue Voix 4 Métrique Liens externes (en) Partitions et informations sur IMSLP (en) La fugue jouée et animée (bach.nau.edu) Prélude et fugue en sol mineur (BWV 885) Prélude et fugue en sol dièse mineur (BWV 887) modifier Le prélude et fugue en la-bémol majeur, BWV 886 est le dix-se...

Metropolitan rail project in Melbourne, Australia Western Rail PlanMap of Rail Lines in Melbourne's West that go through Sunshine. Blue means the line will be or is electrified, purple means it is a regional line.OverviewStatusCancelledWebsiteOfficial website The Western Rail Plan is a metropolitan rail infrastructure project being undertaken in Melbourne, Australia. The project was initially announced during the 2018 Victorian state election by the State Government. It includes the electrifi...

Executive branch of government made up of the President and the Cabinet of Singapore Government of SingaporeOverviewEstablished9 August 1965; 58 years ago (1965-08-09)StateRepublic of SingaporeLeaderPrime Minister of SingaporeAppointed byPresident of SingaporeMain organCabinet of SingaporeMinistries16Responsible toParliament of SingaporeWebsitewww.gov.sg This article is part of a series onPolitics of Singapore Government Constitution of Singapore Law Human rights Legislature...

Aboriginal rock painting of Mimi spirits in the Anbangbang gallery at Nourlangie Rock Mimis (or Mimih spirits [1]) are fairy-like beings of Arnhem Land in the folklore of the Aboriginal Australians of northern Australia. They are described as having extremely thin and elongated bodies, so thin as to be in danger of breaking in case of a high wind. To avoid this, they usually spend most of their time living in rock crevices.[1] According to Aboriginal folklore, Mimi had human f...

Municipality in Asturias, SpainVegadeo A Veiga (Eonavian)MunicipalitySuarón river at Vegadeo Coat of armsVegadeoLocation in SpainCoordinates: 43°28′N 7°3′W / 43.467°N 7.050°W / 43.467; -7.050Country SpainAutonomous community AsturiasProvinceAsturiasComarcaEo-NaviaJudicial districtCastropolCapitalVegadeoGovernment • AlcaldeJuan de la Cruz Antolín Rato (PSOE)Area • Total80.69 km2 (31.15 sq mi)Highest elevati...

Este artigo ou seção pode conter informações desatualizadas. Se tem conhecimento sobre o tema abordado, edite a página e inclua as informações mais recentes, citando fontes fiáveis e independentes. —Encontre fontes: ABW • CAPES • Google (N • L • A) As referências deste artigo necessitam de formatação. Por favor, utilize fontes apropriadas contendo título, autor e data para que o verbete permaneça verificável. (Jan...

2011 comic book storyline by DC Comics Reign of DoomsdayThe principal characters of the Reign of Doomsday crossover, art by Kenneth Rocafort.PublisherDC ComicsPublication dateJanuary 2011Genre Superhero Crossover Creative teamWriter(s)Steve LyonsDan DiDioJames RobinsonJeff LemirePaul CornellPenciller(s)Ed BenesPhilip TanBrett BoothMiguel SepulvedaMarco RudyKenneth RocafortAxel Giménez Reign of Doomsday is a 2011 comic book crossover storyline published by DC Comics that ran through the Super...

Saeid Ezatolahi oleh Shahabodin Vajedi, 2018Informasi pribadiNama lengkap Saeid EzatolahiTanggal lahir 1 Oktober 1996 (umur 27)Tempat lahir Bandar-e Anzali, IranTinggi 193 cm (6 ft 4 in)Posisi bermain GelandangInformasi klubKlub saat ini RostovKarier junior2010 - 2011 MalavanKarier senior*Tahun Tim Tampil (Gol)2012 - 2014 Malavan 19 (0)2014 - 2015 Atletico Madrid C 2015 – 2017 Rostov 11 (1)2017 → Anzhi Makhachkala (pinjaman) 10 (0)2017 - 2018 → FC Amkar Perm (pinjama...

Joaquín II Héctor Margrave elector de Brandeburgo Joaquín II Héctor, príncipe elector de Brandeburgo, pintado por Lucas Cranach el Viejo en 1520Reinado 1535 - 1571Predecesor Joaquín I NéstorSucesor Juan JorgeInformación personalNacimiento 13 de enero de 1505CöllnFallecimiento 3 de enero de 1571 (65 años)Palacio de KöpenickReligión Católica (hasta 1539)Luterana (entre 1539 y 1555)FamiliaDinastía Casa de HohenzollernPadre Joaquín I Néstor de BrandeburgoMadre Isabel de DinamarcaC...