Segundo momento de área
|
Read other articles:

Belisario Torres Otoya Belisario Torres en 1900. Ministro de Hacienda del Ecuador 21 de marzo de 1908-16 de julio de 1908Presidente Eloy AlfaroPredecesor Jorge Marcos AguirreSucesor Tomás Gagliardo Aubert Información personalNombre de nacimiento Belisario Viterbo Torres OtoyaNacimiento 4 de septiembre de 1863 Samborondón, Guayas, EcuadorFallecimiento 21 de enero de 1912 (48 años) Quito, EcuadorCausa de muerte Homicidio Sepultura Cementerio de San DiegoNacionalidad EcuatorianaLengua m...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2019) فيليس دراموند بيثيون معلومات شخصية اسم الولادة (بالإنجليزية: Phyllis Dagmar Drummond Sharpe) الميلاد 27 فبراير 1899 الوفاة 12 ديسمبر 1982 (83 سنة) وانكا مواطنة نيوزي

HTMS Chakri Naruebet sedang berlayar di Laut China Selatan di awal Tahun 2001 Sejarah Thailand Nama HTMS Chakri NaruebetAsal nama In honour of the Chakri DynastyDipesan 27 Maret 1992Pembangun Bazán, Ferrol, SpanyolBiaya 336 Juta Dollar Amerika SerikatPasang lunas 12 Juli 1994Diluncurkan 20 Januari 1996Mulai berlayar 27 Maret 1997Pelabuhan daftar SattahipMotto Rule The Sky, Rule The Sea, Chakri Naruebet. (ครองเวหา ครองนที จักรีนฤเบศร)Status ...

Pour les articles homonymes, voir Bourges (homonymie). Ne doit pas être confondu avec Bourgès ou Maurice Bourgès-Maunoury. Bourges De haut en bas, de gauche à droite : cathédrale Saint-Étienne, Palais Jacques-Cœur, ancienne Maison de la culture, marais de Bourges et quartiers nord. Blason Logo Administration Pays France Région Centre-Val de Loire Département Cher (préfecture) Arrondissement Bourges(chef-lieu) Intercommunalité CA Bourges Plus(siège) Maire Mandat Yann Galut (DV...

Persatuan Sosialis Arab الاتحاد الاشتراكي العربيSekretaris JendralGamal Abdul Nasir(1962–1965)Ali Sabri(1962–1971)Anwar Sadat(1971–1978)KetuaGamal Abdul Nasir(1962–1970)Dibentuk1962 (1962)Dibubarkan1978 (1978)Diteruskan olehPartai Demokratik NasionalKantor pusatKairo, MesirSayap pemudaOrganisasi Pemuda Sosialis Republik Persatuan ArabIdeologiNasionalisme ArabSosialisme ArabPan-ArabismeNasserismePosisi politikSayap kiriPolitik MesirPersatuan So...

University in Guangzhou, China This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sun Yat-sen University of Medical Sciences – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this template message) Sun Yat-sen University of Medical SciencesSimplified Chinese中山医科�...

2019 single by Black Eyed Peas and J Balvin Ritmo (Bad Boys for Life)Single by Black Eyed Peas and J Balvinfrom the album Bad Boys for Life – The Soundtrack and Translation ReleasedOctober 11, 2019Recorded2019Genre Hip hop pop reggaeton Length3:42 (single version)3:34 (album version)LabelEpicSongwriter(s) William Adams Allan Pineda José Álvaro Osorio Balvín Keith Harris Annerley Gordon Francesco Bontempi Giorgio Spagna Michael Gaffey Peter Glenister[1] Producer(s) will.i.am Keith...

Stimulant drug and appetite suppressant MazindolClinical dataTrade namesMazanor, SanorexAHFS/Drugs.comMicromedex Detailed Consumer InformationRoutes ofadministrationOralATC codeA08AA05 (WHO) Legal statusLegal status AU: S4 (Prescription only) BR: Class B2 (Anorectic drugs)[1] CA: Schedule IV DE: Anlage II (Authorized trade only, not prescriptible) US: Schedule IV Schedule IV (International)[how?] Pharmacokinetic dataBioavailability93%Metaboli...

Scottish Sunday newspaper based in Glasgow This article is about the Scottish newspaper. For other uses, see Sunday Herald (disambiguation). Sunday HeraldFront cover of the final edition published in 2018TypeWeeklyFormatCompactOwner(s)NewsquestPublisherHerald & Times GroupEditorNeil Mackay (2015–2018)Founded2 February 1999 (1999-02-02)Political alignmentPro-independenceCentre-leftLanguageEnglishCeased publication2 September 2018; 5 years ago (2018-09-02)...

Israeli mathematician Zlil Sela Zlil Sela is an Israeli mathematician working in the area of geometric group theory. He is a Professor of Mathematics at the Hebrew University of Jerusalem. Sela is known for the solution[1] of the isomorphism problem for torsion-free word-hyperbolic groups and for the solution of the Tarski conjecture about equivalence of first-order theories of finitely generated non-abelian free groups.[2] Biographical data Sela received his Ph.D. in 1991 fro...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The National Anthem film – news · newspapers · books · scholar · JSTOR (August 2016) (Learn how and when to remove this template message) 1999 Chinese filmThe National AnthemDirected byWu ZiniuStarringHe ZhengjunChen KunRelease date October 7, 19...

Novel by John Gardner (British writer) Death Is Forever First editionAuthorJohn GardnerCountryUnited KingdomLanguageEnglishSeriesJames BondGenreSpy fictionPublisherHodder & StoughtonPublication date1992Media typePrint (Hardcover and Paperback)Pages224 pp (first edition, hardback)ISBN0-340-54816-9 (first edition, hardback)OCLC26721121 Death Is Forever, first published in 1992, was the twelfth novel by John Gardner to feature Ian Fleming's secret agent, James Bond (including Gardner's ...

UNESCO World Heritage Site in northern India Hill Forts of RajasthanUNESCO World Heritage SiteAmber Fort at JaipurLocationRajasthan, IndiaIncludes Chittor Fort Kumbhalgarh Fort Ranthambore Fort Gagron Fort Amber Fort Jaisalmer Fort Mehrangarh Fort CriteriaCultural: (ii), (iii)Reference247revInscription2013 (37th Session)123456Show map of Rajasthan123456Show map of India Hill Forts of Rajasthan are six forts, spread across Rajasthan state in northern India. They have been clustered as a series...

Neighbourhood of Dublin This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: South Lotts – news · newspapers · books · scholar · JSTOR (January 2020) (Learn how and when to remove this template message) View of South Lotts from top floor of the Google Docks (Montevetro) building. The corner of South Dock Street P...

American actor Trevor AshleyAshley at the 2015 Helpmann AwardsBorn (1980-02-27) 27 February 1980 (age 43)AustraliaOccupationActorYears active1998–present Trevor Ashley (born 27 February 1980) is an Australian musical theatre actor, cabaret and drag artist based in Sydney. He also has appeared on television in The Very Trevor Ashley Show. Early life Ashley grew up in the south of Sydney and studied at the Shopfront a contemporary theatre.[citation needed] There he worked wi...
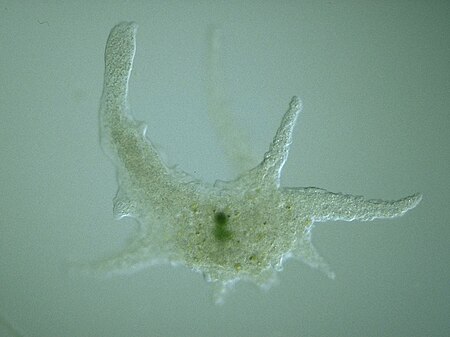
Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari Amoebozoa di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat pula: panduan penerjemahan a...

こみやま りな小宮山 莉渚 第35回東京国際映画祭にて(2022年10月24日)プロフィール生年月日 2005年7月14日現年齢 18歳出身地 日本・宮城県公称サイズ(2022年10月時点)身長 / 体重 169 cm / ― kg 単位系換算身長 / 体重5′ 7″ / ― lb活動デビュー 2018年モデル内容 一般事務所 スターダストプロモーションモデル: テンプレート - カテゴリ 小宮山 莉渚(こみやま りな、2005年7月14�...

Šiam straipsniui ar jo daliai trūksta išnašų į šaltinius.Jūs galite padėti Vikipedijai pridėdami tinkamas išnašas su šaltiniais. Tokajaus regionasjap. 中部地方 = Tōkai-chihō Gyventojų (2010) 15 138 397 Plotas 29 316,53 km² Tankumas (2010) 516 žm./km² Tokajus (jap. 東海方 = Tōkai-chihō) – Japonijos regionams Čiūbu, Kantui ir Kansajui priklausantis subregionas. Regionui priskiriamos Šidzuokos, Aičio, Mijės pr...

American sculptor Jack E. Anderson's Snowshoe Priest (1969) sculpture of Bishop Frederic Baraga Jack E. Anderson (September 10, 1929 – December 5, 1993) was a metal sculptor of large commemorative statues that are roadside attractions in the Midwestern United States. His work includes the 36-foot (11 m) tall figure that is part of the 81-foot (25 m) Iron Man statue at the entrance to the Ironworld Discovery Center, 1.3 kilometers outside Chisholm, Minnesota, and a sta...
В Википедии есть статьи о других людях с фамилией Вольски. Войтек Вольский Позиция центральный нападающий, крайний нападающий Рост 191 см Вес 91 кг Хват левый[d] Страна Канада Польша Дата рождения 24 февраля 1986(1986-02-24) (38 лет) Место рождения Забже, Польша Кар�...





















