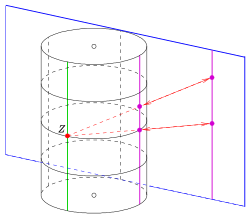
Plano de Laguerre
|
Read other articles:

Rani AgustinaRani Agustina AngrainiLahirRani Agustina Angraini24 Agustus 1993 (umur 30) Jakarta, IndonesiaNama lainAgustina Angraini, Rani Agustina, Rani AgustinePekerjaanArtis, modelTahun aktif2008 - sekarang Rani Agustina Angraini (lahir 24 Agustus 1993) merupakan seorang artis berkebangsaan Indonesia. Karier Rani Agustine dikenal luas oleh masyarakat sejak membintangi sinetron Kepompong dengan karakter antagonisnya. Selain itu, Rani juga mendapatkan peran sebagai Eris di fil...

Eparki BuchachEparchia Bucacensis UcrainorumБучацька єпархія Української греко-католицької церквиLambang BuchachLokasiNegara UkrainaProvinsi gerejawiEparki Agung Ternopil–ZborivKantor pusatChortkiv, Oblast Ternopil, UkrainaStatistikLuas4.829 km2 (1.864 sq mi)Populasi- Total- Katolik(per 2012)382.980211,314 (55.2%)InformasiGereja sui iurisGereja Katolik Yunani UkrainaRitusRitus BizantiumPendirian21 Juli 2...

Surabaya BIN SamatorNama lengkapSurabaya Badan Intelijen Negara SamatorNama pendekSamatorSBSDidirikan2002 (sebagai Surabaya Flame)[1][2]ArenaDriyorejo, GresikPemilikBINSamator Indo GasManajerHadi SampurnoPelatih Ryan MasajediKaptenRivan NurmulkiLigaProligaLivoli Divisi Utama2022Ke-2Seragam Kandang Tandang Surabaya BIN Samator adalah klub bola voli putra Indonesia yang berbasis di Kota Surabaya, Jawa Timur dan berdiri sejak tahun 2002. Klub ini dimiliki oleh Samator Indo Gas da...

Лукум Шматочки лукумуТип ДесертПоходження Османська імперіяНеобхідні компоненти крохмаль і цукорЕнергетичнацінність(на порцію) 316 ккал (1323 кДж)Харчовацінність(на порцію) Білки: 0,8 г Жири: 0,7 г Вуглеводи: 79,4 г Глікемічний індекс 75 (високий...

селище Хавенка Хавенка Країна Росія Суб'єкт Російської Федерації Воронезька область Муніципальний район Панінський район Поселення Панінське міське поселення Код ЗКАТУ: 20235551003 Код ЗКТМО: 20635151116 Основні дані Населення ▼ 11 (2010)[1] Поштовий індекс 396175 Географічні коо

Cette liste est une ébauche concernant le Puy-de-Dôme et les monuments historiques français. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Cet article recense les monuments historiques du Puy-de-Dôme, en France. Statistiques Au 12 février 2023[1], le Puy-de-Dôme compte 874 édifices comportant au moins une protection au titre des monuments historiques, dont 265 sont classés et 651 sont inscrits. Le ...

PammanggangangKoordinat4°41′25.000″LS,119°7′19.000″BTNegaraIndonesiaGugus kepulauanKapoposang, subbagian Kepulauan SpermondeProvinsiSulawesi SelatanKabupatenPangkajene dan KepulauanLuas54.417,8527580 m²PopulasiTak berpenghuni Nomor 44 menunjukkan lokasi Pulau Pammanggangang Pammanggangang atau Pamanggangang adalah nama sebuah pulau kecil tak berpenghuni yang berada di gugusan Kepulauan Kapoposang, subbagian Kepulauan Spermonde, perairan Selat Makassar dan secara administratif ...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: American Latino TV – news · newspapers · books · scholar · JSTOR (February 2021) American TV series or program American Latino TVGenreMagazine-styleDirected byHumberto GuidaPresented byCarolina Trejos (2019–present)Country of originUnited State...

Municipal park in Edmonton, Canada One of Rundle Park's many ponds; this one features a large fountain in the middle. A view towards southwest from a hill in the northern part of Rundle Park. Rundle Park is a municipal park in Edmonton, Canada, and a major park in the North Saskatchewan River Valley parks system. The park overlooks the North Saskatchewan River, and there is a pedestrian bridge that connects Gold Bar Park and Rundle Park together. The park features paved paths, sport amenities...

Голова — термін, який має кілька значень. Ця сторінка значень містить посилання на статті про кожне з них.Якщо ви потрапили сюди за внутрішнім посиланням, будь ласка, поверніться та виправте його так, щоб воно вказувало безпосередньо на потрібну статтю.@ пошук посилань са...

Denmark's governing body for badminton Badminton DenmarkBadminton DanmarkFormation15 January 1930TypeNational Sport AssociationHeadquartersBrøndbyDirectorKristian Langbak[1]AffiliationsBEC, BWFWebsitebadminton.dk Badminton Denmark is the national governing body for the sport of badminton in Denmark. The organization represents above 700 clubs as of 2023.[2] The highest authority in Badminton Denmark is the assembly where each member club is represented. The board of directors...

Beta product from Google Not to be confused with Google Code. This article needs to be updated. Please help update this article to reflect recent events or newly available information. (December 2018) Google Code SearchType of siteSearch engineAvailable inAll languagesOwnerGoogleURLwww.google.com/codesearchLaunchedOctober 5, 2006; 17 years ago (2006-10-05)Current statusDiscontinued as of 15 January 2012 Google Code Search was a free beta product from Google which d...

Rugby union stadium in Darlington, England The Darlington ArenaThe arena as pictured in 2009LocationDarlington, EnglandOwnerDarlington Mowden ParkCapacity25,500[1][2][3]Field size110 by 74 yards (101 m × 68 m)SurfaceGrassConstructionOpened2003Construction cost£18 million[3]TenantsDarlington F.C. (2003–2012)Darlington Mowden Park R.F.C. (2012–) The Darlington Arena is a rugby union stadium, located in Darlington, County Durham. The arena was...

Warren High School is a public high school in Warren, Texas, United States.[1] It is part of the Warren Independent School District, which is located in southern Tyler County and extends into a small portion of northern Hardin County. The Principal is James Swinney[2] with Brianne Dean serving as Assistant Principal.[3] Public school in Warren, Texas, United StatesWarren High SchoolAddress375 FM 3290 S.Warren, Texas 77664United StatesInformationSchool typePublic high s...

Indian footballer V. P. Sathyan Personal informationDate of birth (1965-04-29)29 April 1965Place of birth Mekkunnu, Kannur, Kerala, IndiaDate of death 18 July 2006(2006-07-18) (aged 41)Place of death Chennai, Tamil Nadu, IndiaPosition(s) Full-back, Defensive midfielderYouth career1982 Spirited Youth ClubSenior career*Years Team Apps (Gls)1983 Lucky Star Club 1984–1992 Kerala Police 1992–1993 Mohun Bagan 1994–1995 Kerala Police 1996 Kerala Police International career1985–1995 Indi...

Municipality in Tabasco, MexicoCentlaMunicipalityLocation of the municipality in Tabasco.Country MexicoStateTabascoCapitalFronteraTime zoneUTC-6 (Central Standard Time) • Summer (DST)UTC-5 (Central Daylight Time) Centla is a municipality in the Mexican state of Tabasco in south-eastern Mexico.[1] References ^ -. Enciclopedia de los Municipios de México. Instituto Nacional para el Federalismo y el Desarrollo Municipal. Retrieved January 4, 2010. This article about a l...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Internet Histories – news · newspapers · books · scholar · JSTOR (March 2023) This article relies...

Ir. H.Joko WidodoWali Kota Surakarta ke-16Masa jabatan28 Juli 2005 – 1 Oktober 2012Penguasa monarkiPakubuwana XIIIPresidenSusilo Bambang YudhoyonoGubernurMardiyantoAli MufizBibit WaluyoWakilF.X. Hadi RudyatmoPendahuluSlamet SuryantoPenggantiF.X. Hadi Rudyatmo Informasi pribadiLahir21 Juni 1961 (umur 62)Surakarta, Jawa Tengah, IndonesiaKebangsaan IndonesiaPartai politik PDI-PSuami/istriIrianaAnakGibran Rakabuming RakaKahiyang AyuKaesang PangarepAlma materUni...

National highway in India National Highway 102BMap of National Highway 102B in redRoute informationAuxiliary route of NH 102Maintained by NHAILength323 km (201 mi)Major junctionsNorth end NH 2 in ChurachandpurSouth end NH 6 in Keifang LocationCountryIndiaStatesManipur, Mizoram Highway system Roads in India Expressways National State Asian ← NH 102A→ NH 102C National Highway 102B, commonly referred to as NH 102B is a national highway in India.[1][2]...

У этого термина существуют и другие значения, см. Статуя Свободы (значения). Достопримечательность Нью-Йорка Свобода, озаряющая мирангл. Liberty Enlightening the World Статуя Свободы в августе 2018 года 40°41′21″ с. ш. 74°02′40″ з. д.HGЯO Период строительства1876—1886 Дата открыти...