Modus ponendo ponens
|
Read other articles:

Scena Narodowego Teatru Nō w Tokio Narodowy Teatr Nō (jap. 国立能楽堂 Kokuritsu Nōgaku-dō) – otwarty w 1983 roku teatr w Japonii, w którym wystawiane są sztuki nō i kyōgen, położony w dzielnicy Shibuya w Tokio. Wraz z kilkoma innymi scenami mającymi status teatrów narodowych, jest zarządzany przez organizację rządową Japan Arts Council. Klimatyzowany gmach teatru mieści w sobie tradycyjną, zadaszoną scenę nō. Widownia podzielona jest na trzy sektory: sh...

American politician Dan K. WilliamsMember of the Pennsylvania House of Representativesfrom the 74th districtIncumbentAssumed office January 1, 2019 (2019-01-01)Preceded byHarry Lewis Jr. Personal detailsBorn (1956-09-23) September 23, 1956 (age 67)Philadelphia, Pennsylvania, U.S.Political partyDemocraticSpouseBaleria AlstonChildren3Residence(s)Sadsbury Township, Chester County, Pennsylvania, U.S.EducationGeneva College (B.S.) Biblical Theological Seminary (...

Constituent political entities of Zimbabwe Provinces of ZimbabweCategoryUnitary stateLocationRepublic of ZimbabweNumber10 ProvincesPopulations1,200,337 (Bulawayo) – 2,123,132 (Harare Province)Areas1,710 km2 (659 sq mi) (Bulawayo) - 28,967 sq mi (75,025 km2) (Matabeleland North)GovernmentProvincial government, National governmentSubdivisionsDistrict Politics of Zimbabwe Constitution Constitutional history Human rights Government President Emmerson Mnangagwa Vice...

Детмольднім. Detmold герб прапор Князівська замок.Князівська замок. Основні дані 51°56′16″ пн. ш. 8°53′00″ сх. д. / 51.93777777780577765° пн. ш. 8.88333333336107777711276867° сх. д. / 51.93777777780577765; 8.88333333336107777711276867Координати: 51°56′16″ пн. ш. 8°53′00″ сх. д. / 51.9...

NOTA: Esta página é uma lista criada para ser transcluída no artigo Brasil com o objetivo de tornar o carregamento desse artigo mais rápido e simplificar a sua edição. Se a alterar, certifique-se que verifica quais as consequências das alterações nesse artigo. Preste atenção especialmente a imagens e tabelas. Algumas das coisas que não devem ser incluídas: Interwikis. Marcas de manutenção que sejam aplicáveis a todo o artigo. Exemplos: {{Sem infocaixa}}, {{Sem imagem}}, {{Sem ...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يونيو 2020) في الاقتصاد السياسي، يعد إزالة السلعنة أو نزع السلعية[1] (بالإنجليزية: Decommodification)، هو قوة الاستحقاقات الاجتماعية ودرجة تحصين المواطنين من تبعية السوق.[2...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2018) اضغط هنا للاطلاع على كيفية قراءة التصنيف شابرة الماء المرتبة التصنيفية جنس التصنيف العلمي فوق النطاق حيويات مملكة عليا حقيقيات النوى مملكة...

Early settlement on present-day Singapore For the sovereign wealth fund based in Singapore, see Temasek Holdings. For area in Bandar Seri Begawan, Brunei, see Kampong Tumasek. Part of Mao Kun map from Wubei Zhi which is based on the early 15th century navigation maps of Zheng He showing Temasek (淡馬錫) at the top left. Part of the Early history of Singapore Topynymy Sabana Temasek • Long Ya Men • Ban Zu Malay Annals Kingdom of Singapura • ...
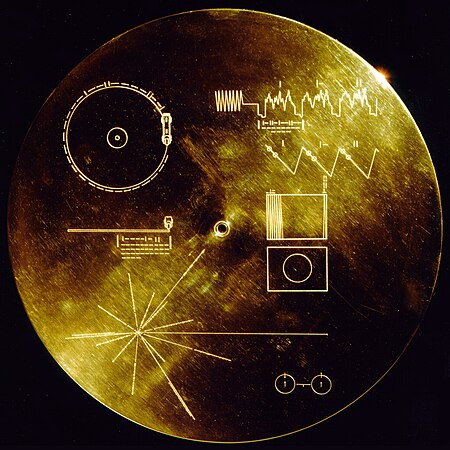
لوحة فوياجر الذهبية مطلية بالذهب. الطلي بالذهب هو شكل خاص من أشكال الطلي الكهربائي يتم فيه وضع ترسيب طبقة رقيقة من الذهب على سطح سبيكة أو فلز آخر مثل النحاس أو الفضة (في حال طلي الفضة بالذهب نحصل على الفضة المذهبة). يمكن أجراء عملية الطلي بالذهب بوسائل أخرى غير الطلي الكهربا�...

Archive, history museum in Brooklyn, New YorkLesbian Herstory ArchivesLogoEstablished1974Location484 14th St.Park Slope, Brooklyn, New York 11215Coordinates40°39′42.79″N 73°58′49.2″W / 40.6618861°N 73.980333°W / 40.6618861; -73.980333TypeArchive, history museumPublic transit access New York City Subway: 15th Street – Prospect Park ( trains) New York City Bus: B61, B67, B68, B69 Websitelesbianherstoryarchives.orgHistoric site New York City Landm...

Aek NatasKecamatanPeta lokasi Kecamatan Aek NatasNegara IndonesiaProvinsiSumatera UtaraKabupatenLabuhanbatu UtaraPemerintahan • Camat-Populasi • Total27,550 jiwa (2.001) jiwaKode Kemendagri12.23.07 Kode BPS1223040 Luas678 km²Desa/kelurahan12 Aek Natas adalah sebuah kecamatan di Kabupaten Labuhanbatu Utara, Sumatera Utara, Indonesia. lbsKecamatan Aek Natas, Kabupaten Labuhanbatu Utara, Sumatera UtaraKelurahan Bandar Durian Desa Adian Torop Kampung Yaman Pangkalan ...

Understanding that non-Malays can be citizens of Malaysia if they accept a special role for Malays This article is part of a series on thePolitics ofMalaysia Head of State Yang di-Pertuan Agong Abdullah of Pahang Conference of Rulers Legislature Parliament of Malaysia 15th Parliament Senate (Dewan Negara) President Wan Junaidi Tuanku Jaafar House of Representatives (Dewan Rakyat) Speaker Johari Abdul Leader of the Government Anwar Ibrahim Leader of the Opposition Hamzah Zainudin Executive Cab...

Peta pembagian wilayah di Jepang. Dari timurlaut ke baratdaya: Hokkaidō (merah), Tōhoku (kuning), Kantō (hijau), Chūbu (sian), Kansai (violet), Chūgoku (jingga), Shikoku (ungu), dan Kyūshū & Okinawa (abu-abu). Pembagian administratifJepang Tingkat Prefektur Prefektur Tingkat subprefektur Subprefektur Distrik Tingkat Kotamadya Kota terpilih Kota inti Kota khusus (dihapus) Kota Distrik kota (Tokyo) Kota kecil Desa Tingkat Sub-kotamadya Distrik kota lbsSelain pembagian wilayah adminis...

Muslim descendants of Rajputs This article may require copy editing for grammar, style, cohesion, tone, or spelling. You can assist by editing it. (April 2023) (Learn how and when to remove this template message) Muslim RajputsRegions with significant populations India and PakistanLanguagesPunjabiSindhiUrduMewatiPahari-PothwariReligion IslamRelated ethnic groupsRajputs and other Indo-Aryan peoples Muslim Rajputs or Musalman Rajpoots are the descendants of Rajputs in the northern re...

Japanese baseball player Baseball player Kodai Sakurai桜井 広大outfielderBorn: (1983-07-01) July 1, 1983 (age 40)Yasu, Shiga, JapanBats: RightThrows: RightNPB debutMay 18, 2007, for the Hanshin TigersNPB statistics (through 2011)Batting average.273Hits225Home runs30RBIs116 Teams Hanshin Tigers (2002 – 2011) Last updated on: January 21, 2012 Kodai Sakurai (桜井 広大, Sakurai Kōdai, born July 1, 1983) is a former Japanese baseball player from Yasu, Shiga Prefectur...

Term in art history for a painting showing a small group of people enjoying themselves Willem Pietersz. Buytewech, Merry Company, c. 1620, apart from the maid an all-male group Merry company is the term in art history for a painting, usually from the 17th century, showing a small group of people enjoying themselves, usually seated with drinks, and often music-making. These scenes are a very common type of genre painting of the Dutch Golden Age and Flemish Baroque; it is estimated that nearly ...

В Википедии есть статьи о других людях с такой фамилией, см. Шереметев; Шереметев, Василий; Шереметев, Василий Петрович.Василий Петрович Шереметев Дата рождения неизвестно Место рождения неизвестно Дата смерти 1659(1659) Место смерти Москва Подданство Русское царство Р...

Video game subscription service by Apple Inc Apple ArcadeDeveloperApple Inc.TypeVideo game subscription serviceLaunch dateSeptember 19, 2019; 4 years ago (2019-09-19)Platform(s)iPhone, iPad, iPod Touch, Mac, Apple TVOperating system(s)iOS 13 or later, iPadOS 13 or later, macOS Catalina or later, tvOS 13 or laterStatusActivePricing modelUS$6.99 per month or US$49.99 annuallyWebsiteApple Arcade Apple Arcade is a video game subscription service offered by Apple Inc. It is avail...

Italian euro coins have a design unique to each denomination, though there is a common theme of famous Italian works of art throughout history. Each coin is designed by a different designer, from the 1 cent to the 2 euro coin they are: Eugenio Driutti, Luciana De Simoni, Ettore Lorenzo Frapiccini, Claudia Momoni, Maria Angela Cassol, Roberto Mauri, Laura Cretara and Maria Carmela Colaneri. All designs feature the 12 stars of the EU, the year of imprint, the overlapping letters RI for Repubbli...







