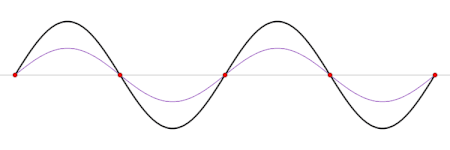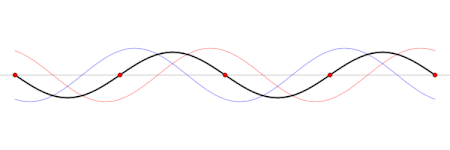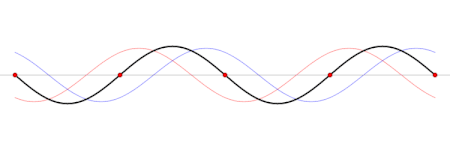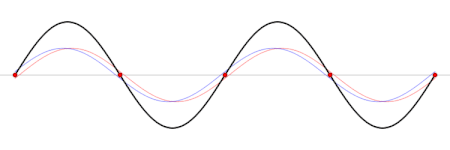
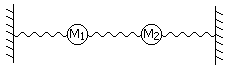Modo normal
|
Read other articles:

Planodes denticornis Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Genus: Planodes Spesies: Planodes denticornis Planodes denticornis adalah spesies kumbang tanduk panjang yang tergolong famili Cerambycidae. Spesies ini juga merupakan bagian dari genus Planodes, ordo Coleoptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Larva kumbang ini biasanya mengebor ke dalam kayu dan dapat menyebabkan kerusakan pada batang kayu ...

Mont d'OrView from the crest towards the southHighest pointElevation1,463 m (4,800 ft)Prominence368 m (1,207 ft)[1]Parent peakCrêt de la NeigeIsolation4.8 km (3.0 mi)[2]Coordinates46°43′39″N 06°21′25″E / 46.72750°N 6.35694°E / 46.72750; 6.35694GeographyMont d'OrLocation in France LocationDoubs, France (mountain partially in Switzerland)Parent rangeJura Mountains Mont d'Or (French: Le Mont d'Or) is a mounta...

Mit suffrage universel (französisch für Allgemeines Wahlrecht) beschriftete Wahlurne, über die ein Löwe wacht. Pariser Denkmal zur Republik (1883). Bronzebildwerk von Léopold Morice. Das allgemeine Wahlrecht ist eines der wichtigsten Merkmale moderner Demokratien. Darunter versteht man, dass alle Bürger grundsätzlich das gleiche Wahlrecht besitzen. Dennoch gelten in allen Demokratien Ausschlussgründe für bestimmte Personengruppen. Beispielsweise muss der Wähler oder Gewählte Staats...

Samantha Achterberg Información personalNacimiento 27 de marzo de 1992 (31 años)Denver (Estados Unidos) Nacionalidad EstadounidenseInformación profesionalOcupación Pentatleta moderno Carrera deportivaDeporte Pentatlón moderno Representante de Estados Unidos [editar datos en Wikidata] Samantha Achterberg (Estados Unidos, 27 de marzo de 1992) es una pentatleta moderna estadounidense.[1][2] Trayectoria deportiva En 2019, ganó la medalla de plata en la categoría de ...

Irregular soldiers in Habsburg Croatia Uskok redirects here. For the Croatian law enforcement institution, see USKOK. Uskoci redirects here. For other uses, see Uskoci (disambiguation). Uskoks / UskociStitch with Uskok-ships chasing a large ship.Museum of Fortress Nehaj in Senj, Croatia.LeadersNumerous; notable leaders include: Petar Kružić (Klis) Ivan Lenković (Senj) Dates of operation1520s–1618HeadquartersMobile, two most famous: Klis Fortress in Klis (origin) Nehaj Fortress in Senj (l...

Ethnic group native of Meglenia, in Greece and North Macedonia Megleno-RomaniansTotal population5,000–20,000Regions with significant populations Greece4,000 North Macedonia1,000 Turkey4,000–5,000[1] Romania (Dobruja)1,200 Serbia (Banat)UnknownLanguagesMegleno-Romanian, Greek, MacedonianReligionOrthodox Christianity, Sunni Islam (in Turkey)Related ethnic groupsAromanians, Istro-Romanians, Romanians The Megleno-Romanians, also known as Meglenites (Megleno Ro...

Kirwan State High School, 2017 Annual Report Kirwan State High School is a coeducational state school located in Kirwan, Townsville, Queensland, Australia, approximately 12 kilometres (7 mi) from the Townsville CBD. In 2017, it has 1997 students with 156 teachers (145 full-time equivalent) and 75 non-teaching staff (59 full-time equivalent),[1] making it the largest high school in North Queensland. It is located in the former city of Thuringowa.[2] History The school enro...

Wilhelm II Landgraf Hesji-Kassel Okres od 1821do 1847 Poprzednik Wilhelm I Następca Fryderyk Wilhelm I Dane biograficzne Dynastia heska Data i miejsce urodzenia 28 lipca 1777 Hanau Data i miejsce śmierci 20 listopada 1847 Frankfurt nad Menem Ojciec Wilhelm I Matka Wilhelmina Karolina Oldenburg Żona Augusta Pruska Dzieci Wilhelm FryderykKarolina FryderykLuiza FryderykaFryderyk Wilhelm I, elektor Hesji-KasselMaria FryderykaFryderyk Wilhelm Ferdynand Odznaczenia Multimedia w Wikimed...

French footballer The topic of this article may not meet Wikipedia's notability guideline for sports and athletics. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: Virgile Gaillard – news · newspapers · books ·...

依存性逆転の原則または依存関係逆転の原則(dependency inversion principle)とは[1]、オブジェクト指向設計の用語であり、ソフトウェアモジュールの疎結合を確立する特別な形態を表現したコンセプトである。SOLIDの五原則の一つとして知られる。 オブジェクト指向における従来の依存関係とは、上位モジュールから下位モジュールへの方向性であり、仕様定義を担う...

Telecommunications company in the Philippines PLDT, Inc.Logo used since June 13, 2016The Ramon Cojuangco Building in Makati, the headquarters of PLDT.FormerlyPhilippine Long Distance Telephone Company (1928–2016)TypePublicTraded asPSE: TEL NYSE: PHIIndustryTelecommunicationsFoundedManila, Philippine Islands(November 28, 1928; 95 years ago (1928-11-28))HeadquartersRamon Cojuangco Building, Makati Avenue corner Dela Rosa Street, Legazpi Village, Makati, Metro Manil...

2017 studio album by Electric WizardWizard Bloody WizardStudio album by Electric WizardReleased17 November 2017RecordedApril 2016 – February 2017[1]StudioSatyr IX Recording StudioGenreDoom metalLength43:04Label Spinefarm Witchfinder[2] Producer Jus Oborn Liz Buckingham Electric Wizard chronology Time to Die(2014) Wizard Bloody Wizard(2017) Singles from Wizard Bloody Wizard See You in HellReleased: 2017[3] Wizard Bloody Wizard is the ninth studio album by Engl...

Metro station in Sendai, Japan T12Rokuchonome Station六丁の目駅 Sendai Subway stationThe South 1 entrance in December 2015General informationLocationWakabayashi-ku, Sendai-shi, Miyagi-ken 984-0012JapanCoordinates38°15′04″N 140°56′08″E / 38.2510°N 140.9356°E / 38.2510; 140.9356Operated bySendai City Transportation BureauLine(s)Tōzai LineDistance12.3 km (7.6 mi) from Yagiyama Zoological ParkPlatforms1 island platformTracks2ConstructionStructur...

Southwest Indiana redirects here. For the community in Elkhart County, see Southwest, Indiana. Region in Indiana, United StatesSouthwestern IndianaRegionEvansville skylineCounties of Southwestern IndianaCountry United StatesState IndianaLargest cityEvansvillePopulation474,251 Southwestern Indiana is an 11-county region of southern Indiana, United States located at the southernmost and westernmost part of the state. As of the 2010 census, the region's combined population is 474,251. ...

Painting by Caravaggio David with the Head of GoliathItalian: Davide con testa di GoliaArtistCaravaggioYearc. 1610MediumOil on canvasDimensions125 cm × 101 cm (49 in × 40 in)LocationGalleria Borghese David with the Head of Goliath is a painting by the Italian Baroque artist Caravaggio. It is housed in the Galleria Borghese, Rome.[1] The painting, which was in the collection of Cardinal Scipione Borghese[a] in 1650,[3] has bee...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مايو 2023) المنديل الأخضر هو رمز لحركات حقوق الإجهاض، التي نشأت في الأرجنتين عام 2003 وشاعت منذ عام 2018 في جميع أنحاء أمريكا اللاتينية وبعد ذلك في الولايات المتحدة عام 2022. ا...

CademènecomuneCademène – Veduta LocalizzazioneStato Francia Regione Borgogna-Franca Contea Dipartimento Doubs ArrondissementBesançon CantoneOrnans TerritorioCoordinate47°06′N 6°02′E / 47.1°N 6.033333°E47.1; 6.033333 (Cademène)Coordinate: 47°06′N 6°02′E / 47.1°N 6.033333°E47.1; 6.033333 (Cademène) Superficie3,39 km² Abitanti95[1] (2009) Densità28,02 ab./km² Altre informazioniCod. postale25290 Fuso orarioUT...

Railway station in Pakistan This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Nawabshah railway station – news · newspapers · books · scholar · JSTOR (March 2015) Nawabshah Railway Stationنواب شاہ ریلوے اسٹیشن نواب شاھ ريلوي اسٽيشنGeneral informationCoordinates26°...

For the Baohe river, see Bao River. District in Anhui, People's Republic of ChinaBaohe 包河区DistrictBaohe in HefeiHefei in AnhuiCoordinates: 31°47′35″N 117°18′35″E / 31.7931°N 117.3097°E / 31.7931; 117.3097CountryPeople's Republic of ChinaProvinceAnhuiPrefecture-level cityHefeiArea • Total294.94 km2 (113.88 sq mi)Population (2019) • Total982,600 • Density3,300/km2 (8,600/sq mi)Time zoneUTC+8 (...

American agrochemical manufacturer CF Industries Holdings, Inc.TypePublic companyTraded asNYSE: CFS&P 500 componentIndustryChemicalsFounded1946; 77 years ago (1946)HeadquartersDeerfield, Illinois, USArea servedNorth AmericaKey peopleTony Will (CEO)ProductsFertilizerRevenue US$4.124 billion (2020)[1]Operating income US$598.0 million (2020)[1]Net income US$317.0 million (2020)[1]Total assets US$12.172 billion (2020)[1]Total equity US$2....