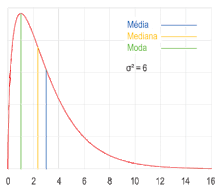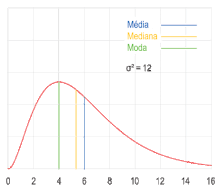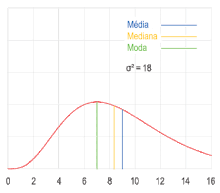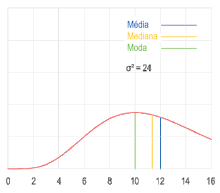
Moda (estadística)
|
Read other articles:

American politician Berkley BedellMember of the U.S. House of Representativesfrom Iowa's 6th districtIn officeJanuary 3, 1975 – January 3, 1987Preceded byWiley MayneSucceeded byFred Grandy Personal detailsBornBerkley Warren Bedell(1921-03-05)March 5, 1921Spirit Lake, Iowa, U.S.DiedDecember 7, 2019(2019-12-07) (aged 98)Naples, Florida, U.S.Political partyDemocraticSpouse Elinor Healy (m. 1943; died 2017)Children3Al...

1982 single by Japan This article is about the song by Japan. For the musician, see Mark Ritsema. Nightporter7-inch single coverSingle by JapanB-side Ain't That Peculiar (7) Methods of Dance (12) Released12 November 1982 (1982-11-12)RecordedAugust – September 1980StudioAIR (London)GenreNew wavesynthpopLength 5:01 (7) 6:48 (12) 6:57 (original Gentlemen Take Polaroids album version) LabelVirginSongwriter(s)David SylvianProducer(s)John PunterJapan singles chronology Life in Toky...

Type of small clock This article is about the type of clock. For the 2009 film, see Timer (film). For the cartoon character, see Time for Timer. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Timer – news · newspapers · books · scholar · JSTOR (May 2010) (Learn how and when to remove this template message) ...

TSPY3 Ідентифікатори Символи TSPY3, CT78, testis specific protein, Y-linked 3, testis specific protein Y-linked 3, TSPY10, TSPY1, TSPY Зовнішні ІД HomoloGene: 87844 GeneCards: TSPY3 Онтологія гена Молекулярна функція • GO:0001948, GO:0016582 protein binding• молекулярна функція Клітинна компонента • клітинне ядро• цитоплазма• компонент клітини Бі�...

Antonio Luna kan verwijzen naar: Antonio Luna (generaal), Filipijns apotheker en generaal. Antonio Luna (voetballer), een Spaans voetballer Bekijk alle artikelen waarvan de titel begint met Antonio Luna of met Antonio Luna in de titel. Dit is een doorverwijspagina, bedoeld om de verschillen in betekenis of gebruik van Antonio Luna inzichtelijk te maken. Op deze pagina staat een uitleg van de verschillende betekenissen van Antonio Luna en verwijzingen daarnaartoe. Bent...

Stoholm Parochie van Denemarken Situering Bisdom Bisdom Viborg Gemeente Viborg Coördinaten 56°30'14,000NB, 9°7'46,999OL Algemeen Inwoners (2004) 2384 Leden Volkskerk (2004) 2230 Overig Kerken Stoholm Kirke Feldingbjerg Kirke Proosdij Skive-Fjends Provsti Pastoraat Kobberup-Feldingbjerg-Nørre Borris-Gammelstrup Foto's Stoholm Kirke Portaal Denemarken Stoholm is een parochie van de Deense Volkskerk in de Deense gemeente Viborg. De parochie maakt deel uit van het bisdom Viborg e...

Article connexe : 26e cérémonie des Critics' Choice Movie Awards. 11e cérémonie des Critics' Choice Television Awards Critics' Choice Television Awards Organisé par la Broadcast Television Journalists Association Détails Date 7 mars 2021 Lieu Santa Monica États-Unis Diffusé sur CW Site web http://www.criticschoice.com Résumé Série la plus nommée The CrownOzark Chronologie 10e cérémonie des Critics' Choice Television Awards 12e cérémonie des Critics' Ch...

Forever LoveSampul CDLagu oleh Tohoshinkidari album TSisi-BDay Moon: ハルダルDirilis14 November 2007FormatCD, CD+DVDGenreJ-PopDurasi6:01 (Versi video musik) 5:27 (Radio edit) 10:18 (versi Album)LabelAvex Trax/Rhythm ZonePenciptaLyrics: Ryoji Sonoda, Composition: Ichiro Fujitani, Arrangement: Jin Nakamura Forever Love adalah singel berbahasa Jepang ke-14 dari Tohoshinki. Singel ini dirilis pada tanggal 14 November 2007.[1] Daftar lagu CD Forever Love Day Moon: ハルダル Forever ...

Bank of New Zealand Atividade Bancária, Serviços financeiros Fundação 2 de julho de 1861 Sede Auckland, Nova Zelândia Pessoas-chave Angela Mentis (CEO) Empregados 5.000 Produtos Serviços bancários, financeiros e de seguros. Empresa-mãe National Australia Bank Website oficial www.bnz.co.nz O Bank of New Zealand (BNZ) é um dos quatro grandes bancos da Nova Zelândia e atua no país desde que o primeiro escritório foi aberto em Auckland em outubro de 1861, seguido pouco depois pe...

artikel ini tidak memiliki pranala ke artikel lain. Tidak ada alasan yang diberikan. Bantu kami untuk mengembangkannya dengan memberikan pranala ke artikel lain secukupnya. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Kamera film digital adalah kamera digital untuk sinematografi digital yang menangkap gambar objek digital daripada kamera film historis, yang tumbuh di film film. Berbeda digital kamera film mengeluaran berbagai format akuisisi yang berbeda. Kamera yang di...

نجوم الشمال الشرقي تأسس عام 2001 البلد ترينيداد وتوباغو الدوري دوري محترفين تي تي المدرب أنغوس إيف تعديل مصدري - تعديل نجوم الشمال الشرقي أو نورث إيست ستارز (بالإنجليزية: North East Stars) هو نادي كرة قدم من ترينيداد وتوباغو، ويلعب في دوري المحترفين. يلعب النادي مب�...

View of the real world with computer-generated supplementary features Not to be confused with Virtual reality or Alternate reality. Virtual Fixtures – first AR system, U.S. Air Force, Wright-Patterson Air Force Base (1992) Augmented reality (AR) is an interactive experience that combines the real world and computer-generated content. The content can span multiple sensory modalities, including visual, auditory, haptic, somatosensory and olfactory.[1] AR can be defined as a system tha...

Art museum of Seoul National University Seoul National University Museum of ArtAlternative namesSNUMoAGeneral informationTypeMuseumAddressSNUMoA, San 56-1, Gwanak-gu, Seoul 151-742Town or citySeoulCountrySouth KoreaConstruction started2003Completed2005InauguratedJune 8, 2006CostBudget: $9.7 million USDClientSeoul National University Museum of ArtHeight17.5 mTechnical detailsFloor area4,478 square metersDesign and constructionArchitecture firmRem Koolhaas, Office for Metropolitan Architecture,...

Julang sulawesi Status konservasi Rentan (IUCN 3.1)[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Coraciiformes Famili: Bucerotidae Genus: Rhyticeros Spesies: Rhyticeros cassidix Nama binomial Rhyticeros cassidix(Temminck, 1823) Julang sulawesi (Rhyticeros cassidix) adalah spesies burung rangkong dalam famili Bucerotidae yang endemik di Sulawesi. Bagi masyarakat Sulawesi, setidaknya terdapat tiga nama lokal untuk menyebut jenis burung ini yaitu Allo, ...

University technical college in Chatham, Kent, EnglandWaterfront University Technical CollegeAddressSouthside Three RoadChatham, Kent, ME4 4FQEnglandCoordinates51°23′50″N 0°32′55″E / 51.3973°N 0.5487°E / 51.3973; 0.5487InformationFormer nameMedway UTCTypeUniversity Technical CollegeEstablished2015 (as Medway UTC)TrustThe Howard Academy TrustDepartment for Education URN146648 TablesOfstedReportsInterim PrincipalPaul CottamAge14 to 19Enrolment278 (March 2...

イオンモール浜松志都呂ÆON MALL HAMAMATSU-SHITORO 地図 店舗概要所在地 静岡県浜松市西区志都呂二丁目37番1号[1]座標 北緯34度41分48秒 東経137度39分05秒 / 北緯34.69667度 東経137.65139度 / 34.69667; 137.65139 (イオンモール浜松志都呂)座標: 北緯34度41分48秒 東経137度39分05秒 / 北緯34.69667度 東経137.65139度 / 34.69667; 137.65139 (イオンモール...

Объект 1015 Объект 1015Б Объект 1015 Классификация Бронетранспортёр Боевая масса, т 9,8 Экипаж, чел. 2 Десант, чел. 19 История Производитель Годы производства 1958 Количество выпущенных, шт. 2 Размеры Длина корпуса, мм 6800 Ширина, мм 2520 Высота, мм 1820 Клиренс, мм 400..450 Бронирование Тип бро...

Untuk orang lain yang bernama sama, lihat William Schroeder. William J. SchroederBiografiKelahiran1932 Jasper (en) Kematian7 Agustus 1986 (53/54 tahun) William J. Schroeder adalah salah satu penerima pertama jantung buatan. Pada tahun 1985, Schroeder penerima kedua Jarvik 7. Setelah 18 hari, ia menderita serangkaian stroke pertama, yang akhirnya membawanya ke dalam keadaan vegetatif. Ia meninggal pada tanggal 6 Agustus 1986 akibat infeksi paru, 620 hari setelah menerima Jarvik 7. Ia adalah or...

Constituency of the National Assembly of France 6th constituency of ParisinlineConstituency of the National Assembly of FranceParis, showing its legislative constituency boundaries from 2012DeputySophia ChikirouLFIDepartmentParis Politics of France Political parties Elections Previous Next The 6th constituency of Paris (French: Sixième circonscription de Paris) is a French legislative constituency in the department of Paris. Like the other 576 French constituencies, it elects one member of t...

Species of moth Citrus peelminer Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Lepidoptera Family: Gracillariidae Genus: Marmara Species: M. gulosa Binomial name Marmara gulosaGuillén & Davis, 2001[1] Marmara gulosa, the citrus peelminer, is a moth of the family Gracillariidae. It is known from California, Arizona, Texas and Florida in the United States and from Cuba. Damage The larvae feed on Nerium oleander, Citrullu...