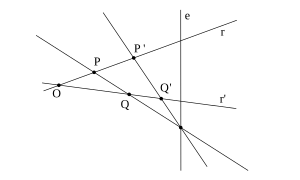
Homología (geometría)
|
Read other articles:

Municipio de Achilles Municipio Municipio de AchillesUbicación en el condado de Rawlins (Kansas). Ubicación de Kansas en Estados Unidos.Coordenadas 39°40′45″N 100°49′44″O / 39.6792, -100.829Entidad Municipio • País Estados Unidos • Estado Kansas • Condado RawlinsSuperficie • Total 132.4 km² • Tierra (99.98%) 132.37 km² • Agua (0.02%) 0.03 km²Altitud • Media 855 m s. n. m.Población ...

Makanan di Warung Tegal Tumpeng, salah satu masakan khas Jawa yang terkenal. Artikel ini merupakan bagian dari seriHidangan Indonesia Hidangan nasional Gado-gado Nasi goreng Rendang Sate Soto Tumpeng Masakan daerah dan budaya Aceh Arab Bali Banjar Batak Gorontalo Betawi Tionghoa India Indo Jawa Madura Makassar Melayu Minahasa Minangkabau Palembang Peranakan Sunda Maluku Papua Bahan Bumbu Penyedap Bumbu kacang Sambal Santan Jenis makanan Makanan Masakan Mi Sup Hidangan penutup Makanan ringan K...

2015 KNSB Dutch Single Distance Championships – Women's 500 mVenueThialf, Heerenveen, NetherlandsDate1 November 2014Competitors24 skatersMedalist men Margot Boer NED Thijsje Oenema NED Bo van der Werff NED←20142016→ 2015 Dutch Single Distance ChampionshipsMen and women500 mmenwomen1000 mmenwomen1500 mmenwomen3000 mwomen5000 mmenwomen10,000 mmenvte The women's 500 meter at the 2015 KNSB Dutch Single Distance Championships took place in Heerenveen at the Thialf ice skati...

Daerah Pertemuan Angin Antar Tropis terlihat seperti gerombolan awan yang mengelilingi bumi di sekitar khatulistiwa Daerah Pertemuan Angin Antar Tropis atau Zona Konvergensi Angin Antar Tropis yang biasa dijuluki oleh para pelaut sebagai daerah angin mati oleh karena cuacanya yang cenderung tidak berangin merupakan suatu wilayah terjadinya pertemuan antara angin pasat timur laut dan angin pasat tenggara. Wilayah ini melingkari permukaan bumi di sekitar daerah khatulistiwa, meskipun posisinya ...

1988 science fiction novel by Lois McMaster Bujold For the song by Madonna, see MDNA (album). Falling Free First editionAuthorLois McMaster BujoldAudio read byGrover GardnerCover artistAlan GutierrezCountryUnited StatesLanguageEnglishSeriesVorkosigan SagaGenreScience fictionPublisherBaen BooksPublication dateApril 1988Media typePaperbackPages307Awards2014 Prometheus Hall of Fame, 1988 Nebula Award for Best NovelISBN0-671-65398-9Preceded byEthan of Athos Followed&...

Wilhelm Blaschke Wilhelm Johann Eugen Blaschke (* 13. September 1885 in Graz, Österreich-Ungarn; † 17. März 1962 in Hamburg) war ein österreichischer Mathematiker und Autor. Seine Arbeiten haben die Entwicklung der modernen Differentialgeometrie entscheidend beeinflusst. Inhaltsverzeichnis 1 Leben 2 Werk 3 Ehrungen und Mitgliedschaften 4 Werke 5 Literatur 6 Online zugängliche Schriften 7 Weblinks 8 Einzelnachweise Leben Wilhelm Blaschke (1930) Sein Vater Josef Blaschke (* 1852 † 1917)...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 徳島市城東中学校 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2021年4月) 徳島市城東中学校 北緯34度04分11秒 東経...

9th episode of the 1st season of Flight of the Conchords What Goes on TourFlight of the Conchords episodeEpisode no.Season 1Episode 9Directed byPaul SimmsWritten byPaul SimmsProduction code109Original air dateAugust 12, 2007 (2007-08-12)Guest appearancesBetsy Morgan (Blonde Girl)Emily Swallow (Becky)David Costabile (Doug)Kate Pierson (Club Owner)Episode chronology ← PreviousGirlfriends Next →New Fans What Goes on Tour is the ninth episode of the HBO comedy se...

AwardOrder of the Sacred TripodOrder of Sacred Tripod with Special Grand CordonAwarded forSignificant contributions to national securityCountry Republic of ChinaPresented by President of the Republic of China (Taiwan)StatusCurrently awardedEstablished15 May 1929PrecedenceNext (higher)Order of Blue Sky and White SunNext (lower)Order of Loyalty and Valour The Order of the Sacred Tripod (寶鼎勳章), also referred to as the Order of the Precious Tripod or Pao Ting, is a military...

American composer Jesse L. Smith GaynorJessie L. Gaynor, from a 1915 publication.Born(1863-02-17)February 17, 1863St. Louis, MissouriDiedFebruary 20, 1921(1921-02-20) (aged 58)St. Louis, MissouriNationalityAmericanOccupationComposerChildrenRose Gaynor Barrett (Rose Fenimore Gaynor) Jesse L. Smith Gaynor (February 17, 1863 - February 20, 1921) was an American composer of children's music. She wrote the music for the well-known children's lullaby The Slumber Boat, in collaboration with the...

This article is about the men's team. For the women's team, see Guernsey women's cricket team. GuernseyAssociationGuernsey Cricket BoardPersonnelCaptainMatthew StokesCoachAndrew CornfordInternational Cricket CouncilICC statusAffiliate (2005) Associate member (2008)ICC regionEuropeICC Rankings Current[1] Best-everT20I 47th 35th (2-May-2019)International cricketFirst international Guernsey v. Jersey (Saint Helier, Jersey; 14 August 1922)Twenty20 InternationalsFirst T20Iv ...

Dutchh association soccer player and manager In this Dutch name, the surname is Ten Cate. Henk ten Cate Cate with Al Jazira in 2016Personal informationFull name Hendrik Willem ten Cate[1]Date of birth (1954-12-09) 9 December 1954 (age 68)Place of birth Amsterdam, NetherlandsPosition(s) Left wingerTeam informationCurrent team SurinameYouth career Ajax De Volewijckers1973–1975 VitesseSenior career*Years Team Apps (Gls)1975–1977 Vitesse 4 (0)1977–1979 VV Rheden ? (?)1979–198...

Bus station opened in 1994 in London This article is about the bus station south of Stratford station opened in 1994. For the bus station opened in 2011 north of the station, see Stratford City bus station. Stratford Bus StationThe bus station in 2009General informationLocationStratfordNewhamOwned byTransport for LondonOperated byLondon BusesBus stands5Bus operators Arriva London Docklands Buses London Central National Express Stagecoach London ConnectionsAdjacent to Stratford stationHistoryO...

Mountain range in Bukidnon, Philippines Kalatungan Mountain RangeKalatungan Mountain Range seen from Barangay Kibangay, Lantapan, BukidnonHighest pointPeakMount KalatunganElevation2,860 m (9,380 ft)Coordinates7°57′18″N 124°48′09″E / 7.95500°N 124.80250°E / 7.95500; 124.80250[1]DimensionsLength38 km (24 mi) east-westWidth19 km (12 mi) north-southArea213.0134 km2 (82.2449 sq mi)Geography Countr...

Transportation system in Riyadh, Saudi Arabia Riyadh BusOverviewOwnerRoyal Commission for Riyadh CityLocaleRiyadhTransit typeBus rapid transitNumber of stations2,900+Websitehttps://www.riyadhbus.sa/OperationBegan operation19 March 2023[1]Number of vehicles800+TechnicalSystem length1,900 km (1,180.61 mi) Riyadh Bus (Arabic: حافلات الرياض) is a 1184-mile comprehensive public bus service network system in Riyadh, Saudi Arabia.[2][3] Background The Ki...

Peta infrastruktur dan tata guna lahan di Komune Langres. = Kawasan perkotaan = Lahan subur = Padang rumput = Lahan pertanaman campuran = Hutan = Vegetasi perdu = Lahan basah = Anak sungaiLangresNegaraPrancisSitus webINSEE Langres adalah sebuah komune di departemen Haute-Marne di Prancis. Lihat pula Komune di departemen Haute-Marne Referensi INSEE lbsKomune di departemen Haute-Marne Ageville Aigremont Aillianville Aingoulaincourt Aizanville Alli...

SpartacusCommemorative coin of the 225th anniversary of the Bolshoi Theater, with a representation of the ballet Spartacus as the centerChoreographerLeonid YakobsonMusicAram KhachaturianPremiere1956 (1956)Kirov Theatre, LeningradOriginal ballet companyKirov BalletCharacters Crassus Spartacus Phrygia Aegina GenreNeoclassical ballet Spartacus (Russian: «Спартак», Spartak) is a ballet by Aram Khachaturian (1903–1978). The work follows the exploits of Spartacus, the leader of the ...

Voce principale: I Cavalieri dello zodiaco - Episode G. Copertina del volume 7 dell'edizione italiana. Questa è la lista dei capitoli e del manga I Cavalieri dello zodiaco - Episode G, scritto e disegnato da Megumu Okada e ispirato all'opera originale di Masami Kurumada. La storia è ambientata sette anni prima degli eventi narrati ne I Cavalieri dello zodiaco e racconta la lotta dei Cavalieri d'Oro, guerrieri che combattono in nome di pace e giustizia, per proteggere la terra dalla minaccia...

Questa voce sull'argomento attori statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Andreas Katsulas in Germania nel 2000 Andrew C. Andreas Katsulas (Saint Louis, 18 maggio 1946 – Los Angeles, 13 febbraio 2006) è stato un attore statunitense di origine greca. È particolarmente noto a livello internazionale per la sua interpretazione dell'ambasciatore G'Kar nella serie televisiva di fantas...

الصفحه دى يتيمه, حاول تضيفلها مقالات متعلقه لينكات فى صفحات تانيه متعلقه بيها. جيورجيو كونتينى معلومات شخصيه الميلاد 4 يناير 1974 (50 سنة)[1][2] سويسرا الطول مركز اللعب مهاجم (كوره قدم) الجنسيه سويسرا الحياة العمليه الفرق نادى سانت جالن (1996–2001)نادى لوزير...