Grado de libertad (física)
|
Read other articles:

German historical painter and sculptor Amor and the Muse, 1807-1811 Portrait of Eberhard by Theodor Rehbenitz Konrad Eberhard (25 November 1768 – 12 March 1859), a German historical painter, better known as a sculptor, was one of the foremost artists of the so-called Nazarene School, which at one time gathered round Friedrich Overbeck in Rome. Biography He was born at Hindelang in Algau, where his father and grandfather were sculptors and carvers. The Elector of Treves and Bishop of Augsbur...

Das Forum Frohner ist ein Kunstmuseum am Minoritenplatz in Stein an der Donau, ein Stadtteil der niederösterreichischen Stadt Krems an der Donau. Das nach dem Künstler Adolf Frohner benannte Museum wurde 2007 eröffnet und befindet sich in einem Bau des Architekten Lukas Göbl, der auf dem Areal des ehemaligen Minoristenklosters errichtet wurde. Betrieben wird das Museum von der Kunstmeile Krems Betriebsges.m.b.H. Im Zentrum der Ausstellungsaktivitäten steht das künstlerische Schaffen von...

NGC 735 الكوكبة المثلث رمز الفهرس NGC 735 (الفهرس العام الجديد)UGC 1411 (فهرس أوبسالا العام)PGC 7282 (فهرس المجرات الرئيسية)2MASX J01563802+3410366 (Two Micron All Sky Survey, Extended source catalogue)IRAS F01537+3356 (IRAS)MCG+06-05-058 (فهرس المجرات الموروفولوجي)UZC J015638.0+341036 (فهرس زفيكي المحدّث)Z 0153.7+3356 (فهرس المجرات وعناقيد المجرا

Sid JordanCuplikan Jordan (kanan) dengan Tom Mix dalam The Coming of the Law (1919)Lahir(1889-08-12)12 Agustus 1889Muskogee, Oklahoma, Amerika SerikatMeninggal30 September 1970(1970-09-30) (umur 81)Hemet, California, Amerika SerikatPekerjaanPemeranTahun aktif1913-1944 Sid Jordan (12 Agustus 1889 – 30 September 1970) adalah seorang pemeran film asal Amerika Serikat. Ia tampil dalam 130 film antara 1913 dan 1944. Filmografi pilihan The Man from Texas (1915) The Golden ...

Indian actor, film director Not to be confused with Rajit Kapur. Rajat KapoorRajat Kapoor at the International Film Festival of India 2014BornNew Delhi, IndiaOccupationsActorfilmmakerplaywrightYears active1989-presentSpouse Meenal Agrawal (m. 1996)Children2 Rajat Kapoor is an Indian actor, filmmaker and playwright who works in Hindi cinema.[1] Early life and career Rajat Kapoor was born in Delhi, India and grew up in Old Delhi.[2] He mainly ...

Lady in the WaterLady in the Water theatrical posterSutradara M. Night Shyamalan Produser Sam Mercer Jose L. Rodriguez M. Night Shyamalan Ditulis oleh M. Night Shyamalan PemeranPaul GiamattiBryce Dallas HowardJeffrey WrightBob BalabanM. Night ShyamalanPenata musikJames Newton HowardPenyuntingBarbara TulliverDistributorWarner Bros.Tanggal rilis21 Juli 2006Durasi110 MenitNegaraBahasa Inggris Anggaran$75,000,000IMDbInformasi di IMDbAMGProfil All Movie Guide Lady in the Water merupakan sebu...

Light rail station in Calgary, Alberta, Canada BrentwoodCTrain stationGeneral informationLocation4099 Crowchild Trail NWCoordinates51°05′15″N 114°07′56″W / 51.08750°N 114.13222°W / 51.08750; -114.13222PlatformsCenter-loading platformConnections8 North Pointe/Foothills Medical Centre9 Dalhousie/Chinook 38 Temple 53 Greenwood/Brentwood 65 Market Mall/Downtown West 82 Nolan Hill 408 Valley Ridge MO Max Orange SaddletowneConstructionStructure typeAt-gradeParkin...

2023 single by Lil Wayne Kat FoodSingle by Lil Waynefrom the album Tha Fix Before Tha VI ReleasedSeptember 1, 2023GenreHip hopLength4:47Label Young Money Republic Songwriter(s) Dwayne Carter Jr. Chris Stein Darryl McDaniels Debbie Harry FnZ Jocelyn Donald Joseph Simmons Missy Elliott Paul Simon Rogét Chahayed Charlie Handsome Producer(s) Rogét Chahayed Charlie Handsome FnZ Lil Wayne singles chronology The Formula (2023) Kat Food (2023) Brand New (2023) Music videoKat Food on YouTube Kat Foo...

Performing arts theater in the City Center District of Downtown Dallas This article is about the Dallas theatre. For other uses, see Majestic Theatre. Majestic TheatreMajestic TheatreAddress1925 Elm St.Dallas, TexasUnited StatesCoordinates32°47′1″N 96°47′40″W / 32.78361°N 96.79444°W / 32.78361; -96.79444OwnerCity of Dallas Office of Arts and CultureOperatorCity of Dallas Office of Arts and CultureTypeTheatreCapacity1,704Acreageless than one acreScreens1Curr...

Возможные положения крыла изменяемой стреловидности F-111. Возможные положения крыла изменяемой стреловидности Су-24. Механизм управления правой поворотной консолью МиГ-23. Крыло изменяемой стреловидности (КИС) — тип конструкции летательного аппарата тяжелее воздуха с...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Woleu-Ntem Province – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) Province of Gabon Province in GabonWoleu-NtemProvince FlagCoat of armsWoleu-Ntem Province in GabonCoordinates: 1°17′36″N ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this article. Unsourced material may be challenged and removed.Find sources: Fairport, New York – news · newspapers · books · scholar · JSTOR (May 2009) (Learn how and when to remove this template message) Village in New York, United StatesFairportVillageThe Fairport Lift BridgeLocation in Monroe County and the state...

A number of memorials have been established to honour people who served in the Korean War (25 June 1950 – 27 July 1953) including : Australia Korean War Memorial, Canberra ANZAC Square, Brisbane Beaudesert War Memorial Cairns War Memorial Esk War Memorial Gair Park Gympie Memorial Park Howard War Memorial Oxley War Memorial Queensland Korean War Memorial Sandgate War Memorial Park St Andrew's Presbyterian Memorial Church, Innisfail Stanthorpe Soldiers Memorial Strathpine Honour Board T...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Unit kendali – berita · surat kabar · buku · cendekiawan · JSTOR Unit kendali (bahasa Inggris: Control Unit) adalah salah satu bagian dari unit pemroses sentral yang bertugas untuk memberikan kendali...

Dr.Imam PrasojoBerkas:Preskon indonesia berprestasi award imam b prasodjo-20080520-002-wawan.jpgLahirImam Budidarmawan PrasojoAlmamaterUniversitas IndonesiaUniversitas BrownPekerjaanDosen, SosiologSuami/istriGitayana Budiardjo Imam Budidarmawan Prasojo (lahir 15 Februari 1960) adalah seorang sosiolog dan tokoh masyarakat dari Indonesia.[1] Saat ini ia menjadi dosen tetap Fakultas Ilmu Sosial dan Ilmu Politik]] (FISIP) Universitas Indonesia. Selain menjadi dosen, Prasodjo juga merupaka...

Buddhist temple in Anhui, China Tiantai Temple天台寺ReligionAffiliationBuddhismSectChan BuddhismLocationLocationMount Jiuhua, Qingyang County, AnhuiCountryChinaGeographic coordinates30°34′21″N 117°46′36″E / 30.572417°N 117.776781°E / 30.572417; 117.776781ArchitectureStyleChinese architectureFounderZhaolian (昭莲)Date established1368Completed1890 (reconstruction) Tiantai Temple (simplified Chinese: 天台寺; traditional Chinese: 天臺寺; piny...
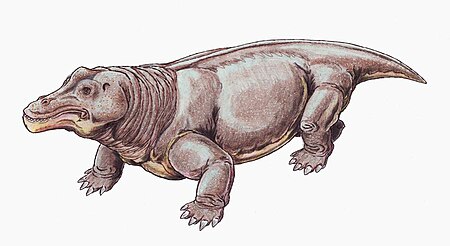
Extinct genus of therapsids StruthiocephalusTemporal range: Capitanian, 265–260 Ma PreꞒ Ꞓ O S D C P T J K Pg N ↓ Life restoration of Struthiocephalus Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Clade: Synapsida Clade: Therapsida Suborder: †Dinocephalia Family: †Tapinocephalidae Genus: †StruthiocephalusHaughton, 1915 Species: †S. whaitsi Binomial name †Struthiocephalus whaitsiHaughton, 1915 Synonyms Moschosaurus Struthi...

この項目では、1972年に設立されたプロレス団体について説明しています。 メサイヤが発売したゲームソフトについては「全日本プロレス (メサイヤのゲーム)」をご覧ください。 セガが発売したゲームソフトシリーズについては「全日本プロレス (セガのゲーム)」をご覧ください。 「全日本プロレス協会」あるいは「全日本女子プロレス」とは異なります。 この記事�...

У этого термина существуют и другие значения, см. Наварра. КоролевствоКоролевство Наварра (Памплона)исп. Reino de Navarra баск. Nafarroako Erresuma фр. Royaume de Navarre окс. Reiaume de Navarra Флаг Герб Наварра и другие государства на Пиренейском полуострове в 1400 году ← → → 824 — 1620 Стол�...

Kenji Haneda Informasi pribadiNama lengkap Kenji HanedaTanggal lahir 1 Desember 1981 (umur 42)Tempat lahir Prefektur Chiba, JepangPosisi bermain BekKarier senior*Tahun Tim Tampil (Gol)2000-2006 Kashima Antlers 2007-2010 Cerezo Osaka 2011-2012 Vissel Kobe * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Kenji Haneda (lahir 1 Desember 1981) adalah pemain sepak bola asal Jepang. Karier Kenji Haneda pernah bermain untuk Kashima Antlers, Cerezo Osaka dan Vissel Kobe. Pra...
















