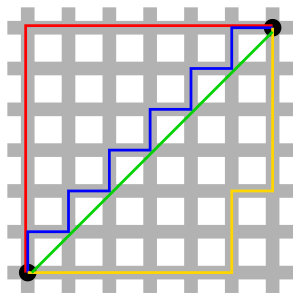
Geometría del taxista
|
Read other articles:

Romy Schneider Romy Schneider, pseudonimo di Rosemarie Magdalena Albach-Retty (Vienna, 23 settembre 1938 – Parigi, 29 maggio 1982), è stata un'attrice austriaca naturalizzata francese. Fu una delle più importanti attrici europee della sua generazione, celebre anche per la grande bellezza e la sua espressività che la portarono a lavorare — a livello internazionale — con alcuni dei più importanti registi della sua epoca.[1][2][3] Indice 1 Biografia 2 Filmografi...

Die historische Siedlung Stahlhausen Stahlhausen ist ein Stadtquartier von Bochum. Namensgeber und prägender Bestandteil ist die Arbeitersiedlung des Bochumer Vereins. Inhaltsverzeichnis 1 Geografie und Verkehr 2 Geschichte 3 Denkmalschutz 4 Weblinks 5 Einzelnachweise Geografie und Verkehr Stahlhausen mit Orts- und Objektbezeichnungen Das Quartier liegt westlich des Stadtzentrums und gehört zu dem Stadtbezirk Mitte. Der genaue Umfang von Stahlhausen ist geografisch nicht genau definiert. De...

ハリカルナッソス(Ἁλικαρνασσός) カリアの古代都市(トルコ) マウソロス霊廟の遺構。「世界の七不思議」のひとつ ハリカルナッソストルコにおける位置トルコの地図を表示ハリカルナッソスハリカルナッソス (エーゲ海)エーゲ海の地図を表示ハリカルナッソスハリカルナッソス (南カリア)南カリアの地図を表示別名 (Bodrum) ハリカルナッソス(古希: Ἁλικαρν

FilmMartino’s SummerDirected byMassimo NataleCinematographyVladan RadovicRunning time90 minutes Martino's Summer (Italian: L’estate di Martino) is a 2010 Italian drama film directed by Massimo Natale.[1][2] It won the Audience Award at the 2011 Flaiano Prizes.[3] It tells the story of a young man in southern Italy who has a romance with a vacationer from the north and learns to surf from an officer on a U.S. military base. Cast Treat Williams: Captain Jeff Clark Lu...

Order of arthropods (fossil) This article is about the order Eurypterida. For the eurypterid family containing Eurypterus itself, see Eurypteridae. EurypteridTemporal range: Darriwilian-Late Permian, 467.3–251.9 Ma PreꞒ Ꞓ O S D C P T J K Pg N Possible Jiangshanian record Fossil specimen of Eurypterus remipes housed at the State Museum of Natural History Karlsruhe in Karlsruhe, Germany Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Subphylum: Chelic...

One of the 234 State Legislative Assembly Constituencies in Tamil Nadu, in India VasudevanallurConstituency for the Tamil Nadu Legislative AssemblyConstituency detailsCountryIndiaRegionSouth IndiaStateTamil NaduTotal electors2,41,748Member of Legislative Assembly16th Tamil Nadu Legislative AssemblyIncumbent Dr. T. Sadhan Tirumalaikumar Party DMKElected year2021 Vasudevanallur is a legislative assembly constituency in Tenkasi district in the Indian state of Tamil Nadu.[1] It...

Public broadcaster for the German states of Thuringia, Saxony, and Saxony-Anhalt This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Mitteldeutscher Rundfunk – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this template message)You can help expand this article with text...

Halaman ini berisi artikel tentang the musical. Untuk kegunaan lain, lihat Guys and Dolls (disambiguasi). Guys & DollsOriginal Cast RecordingMusikFrank LoesserLirikFrank LoesserNaskahJo Swerling Abe BurrowsDiangkat dariThe Idyll of Miss Sarah Brown and Blood Pressure by Damon RunyonProduksi1950 Broadway 1953 West End 1976 Broadway revival 1982 London revival 1992 Broadway revival 2005 West End revival 2008 Australia2009 Broadway revivalPenghargaanTony Award for Best Musical Tony Award for...

Removal of the human foreskin Not to be confused with female circumcision. For the paintings, see The Circumcision. CircumcisionCircumcision surgery with hemostats and scissorsICD-10-PCSZ41.2ICD-9-CMV50.2MeSHD002944OPS-301 code5–640.2MedlinePlus002998eMedicine1015820[edit on Wikidata] Circumcision is a procedure that removes the foreskin from the human penis. In the most common form of the operation, the foreskin is extended with forceps, then a circumcision device may be placed, a...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (June 2019) The Lamentation of Cloris or The Lamentation of Cloris, For the Unkindness of her Shepherd is a broadside ballad, which dates from, by estimation of the English Short Title Catalogue, 1678-1680. The ballad begins, MY Shepherd's unkind,/ alas, what shall I do?. Copies of the ballad can be found at the National Library of Scot...

Cinema in Rayners LaneAce CinemaTypeCinemaLocationRayners LaneCoordinates51°34′26″N 0°22′14″W / 51.573922°N 0.370611°W / 51.573922; -0.370611OS grid referenceTQ 13010 87371AreaHarrowBuilt1936ArchitectF E BromigeArchitectural style(s)Art DecoOwnerZTFE Listed Building – Grade IIOfficial nameAce CinemaDesignated13 March 1981Reference no.1079729 Listed Building – Grade II*Official nameAce CinemaDesignated27 January 1984Reference no.1079729 Locatio...

Tris Speaker, the modern leader in fielding errors as a center fielder In baseball statistics, an error is an act, in the judgment of the official scorer, of a fielder misplaying a ball in a manner that allows a batter or baserunner to advance one or more bases or allows an at bat to continue after the batter should have been put out. The center fielder (CF) is one of the three outfielders, the defensive positions in baseball farthest from the batter. Center field is the area of the outfield ...

Киннорарфа Давида Предполагаемый вид инструмента Классификация Струнный инструмент, Хордофон Родственные инструменты Лира, Арфа, Гусли Медиафайлы на Викискладе Важнейшим визуальным источником киннора является рельеф из Ниневии, выставленный в Британском музее: п�...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (أغسطس 2019) هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسي...

Tringa totanus Archibebe comúnEstado de conservaciónPreocupación menor (UICN)[1]TaxonomíaReino: AnimaliaFilo: ChordataClase: AvesOrden: CharadriiformesFamilia: ScolopacidaeGénero: TringaEspecie: T. totanus(Linnaeus, 1758)Distribución Distribución de Tringa totanus Área de cría. Área de ocupación permanente. Área de migración. Área de invernada.[e...

لمعانٍ أخرى، طالع لواء (توضيح). لواء الرتبة الأعلى فريق الرتبة الأدنى عميد، وعقيد تعديل مصدري - تعديل رتبة لواء هي رتبة عسكرية في الكثير من البلدان معظم جيوش بلدان الكومنولث وعدد من الدول العربية[1][2][3][4] واليابان وألمانيا والولايات المت�...

Human settlement in County Durham, England Human settlement in EnglandEbchesterEbchesterLocation within County DurhamUnitary authorityCounty DurhamCeremonial countyDurhamRegionNorth EastCountryEnglandSovereign stateUnited Kingdom List of places UK England County Durham 54°53′N 1°50′W / 54.883°N 1.833°W / 54.883; -1.833 Derwentcote Steel Furnace The River Derwent near Ebchester. Embleton Pond near the village of Ebchester. Ebchester is a village i...

Norwegian philosopher Ole Martin MoenBorn (1985-04-28) 28 April 1985 (age 38)EducationPhilosophy (PhD)Practical Pedagogy (PPU)Intellectual History (MPhil)Intellectual History (BA)Alma materUniversity of OsloAwardsZapffe Prize (2019)EraContemporary philosophyInstitutionsOslo Metropolitan UniversityUniversity of OsloUniversity of OxfordMain interestsAnimal ethics, bioethics, environmental ethics Websitewww.olemartinmoen.com Ole Martin Moen (Norwegian pronunciation: [ˈû:lə ˈmɑ...

1951 film by Fred de Cordova Bedtime for BonzoOriginal 1951 film posterDirected byFred de CordovaScreenplay byVal BurtonLou BreslowStory byTed BerkmanRaphael David BlauProduced byMichael KraikeStarringRonald ReaganDiana LynnCinematographyCarl E. GuthrieEdited byTed KentMusic byFrank SkinnerColor processBlack and whiteProductioncompanyUniversal International PicturesDistributed byUniversal PicturesRelease dates February 15, 1951 (1951-02-15) (Circle Theatre, Indianapolis) ...

كأس العالم 1962 تفاصيل البطولة الدولة المستضيفة تشيلي المدن 4 المنظم الاتحاد الدولي لكرة القدم مشاركون هيلموت هالر التاريخ 30 مايو – 17 يونيو الفرق 16 (من 3 اتحادات ) الأماكن 4 (في 4 المدن المستضيفة) المراكز النهائية البطل البرازيل (2 ألقاب) الوصيف تشيكوسلوفا�...