Apertura numérica
|
Read other articles:

Мей Вітманангл. Mae Whitman Ім'я при народженні Мей Маргарет ВітманНародилася 9 июня 1988 (35 років)Лос-Анджелес, Каліфорнія, СШАГромадянство СШАДіяльність акторка, кіноакторка, телеакторка, акторка озвученняAlma mater Ribet AcademydРоки діяльності 1994 — тепер. часБатьки Pat MusickdIMDb n...

Logo SCTV Berikut ini adalah daftar penyiar SCTV. Penyiar saat ini Khusus Liputan 6 dan BUSER Azizah Hanum (mantan penyiar NET., Kompas TV dan CNN Indonesia) Beverly Gunawan (sekaligus penyiar di Moji) Dana Paramita (mantan penyiar Kompas TV biro Jawa Tengah, sekaligus penyiar di Moji) Djati Darma (mantan penyiar Astro Awani Indonesia) Gracia Bern Tobing (mantan penyiar TVRI Sumatera Utara) Joy Astro (mantan penyiar RCTI) Nabiel Abiyasha Ramaditya Domas (mantan penyiar BTV sekaligus penyiar d...

De Canadian Battlefields Memorials Commission was een speciale commissie die werd opgericht door het Canadese Lagerhuis na de Eerste Wereldoorlog met het doel herdenkingssites voor Canadese soldaten in te richten in België en Frankrijk. Geschiedenis Maquettes van de ontwerpwedstrijd Winnend ontwerp van Allward Ontwerp van Clemesha In de Eerste Wereldoorlog was Canada nog deels afhankelijk van Groot-Brittannië. Het land werd dan ook mee betrokken in de oorlog en tienduizenden soldaten gingen...

Untuk versi Resmi, lihat YouTube Rewind. Penyuntingan Artikel oleh pengguna baru atau anonim untuk saat ini tidak diizinkan hingga 29 Januari 2024.Lihat kebijakan pelindungan dan log pelindungan untuk informasi selengkapnya. Jika Anda tidak dapat menyunting Artikel ini dan Anda ingin melakukannya, Anda dapat memohon permintaan penyuntingan, diskusikan perubahan yang ingin dilakukan di halaman pembicaraan, memohon untuk melepaskan pelindungan, masuk, atau buatlah sebuah akun. Rewind Indonesia ...

селище Новоєпіфанівка Новоепифановка Країна Росія Суб'єкт Російської Федерації Воронезька область Муніципальний район Панінський район Поселення Краснолиманське сільське поселення Код ЗКАТУ: 20235816006 Код ЗКТМО: 20635416126 Основні дані Населення ▼ 1 (2010)[1] Поштовий інд

Українська націонал-трудова партія Дата заснування 2005Дата ліквідації 2009Офіційний сайт untp.org.ua Украї́нська націона́л-трудова́ па́ртія (УНТП) — націонал-соціалістична молодіжна організація, яка діяла в Україні у 2005—2009 роках. Офіційно міністерством юстиції України за�...

Rexnord CorporationTypeSubsidiaryFounded1891; 132 years ago (1891)FounderChristopher LevalleyHeadquarters511 W Freshwater Way, Milwaukee, United StatesOwnerRegal Rexnord CorporationNumber of employees8,000 (2016)[1]Websitehttps://www.regalrexnord.com/ Rexnord Corporation is a Milwaukee, Wisconsin-based subsidiary of Regal Rexnord Corporation. It was founded in 1891 by Christopher Levalley and incorporated in 1892 as the Chain Belt Company. It had $67.5 million in pro...

Imamat 4Kemah Suci, Biblical illustrations, Sweet Media, 1984KitabKitab ImamatKategoriTauratBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen3← pasal 3 pasal 5 → Imamat 4 adalah bagian dari Kitab Imamat dalam Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen. Termasuk dalam kumpulan kitab Taurat yang disusun oleh Musa.[1][2] Teks Naskah sumber utama: Masoretik, Taurat Samaria, Septuaginta dan Naskah Laut Mati. Pasal ini terdiri dari 35 ayat. Berisi...

1984 film directed by Dedé Santana Os Trapalhões e o Mágico de OrózTheatrical release posterDirected byDedé SantanaVitor LustosaWritten byArnaud RodriguesRenato AragãoVitor LustosaGilvan PereiraProduced byRenato AragãoStarringRenato AragãoDedé SantanaMussumZacariasCinematographyAntônio GonçalvesEdited byDenise FontanaJayme JustoMusic byArnaud RodriguesProductioncompanyRenato Aragão Produções ArtísticasDistributed byEmbrafilmeRelease date June 21, 1984 (1984-06-21...

Italia Romawi (hijau) sebagaimana dibagi oleh Augustus Italia adalah nama bagi semenanjung Italia pada masa Republik dan Kekaisaran Romawi. Istilah Italia meliputi wilayah yang batas-batasnya berubah-ubah seiring waktu. Menurut Strabo, pada awalnya nama tersebut menunjukkan daerah antara Selat Messina dan jalur yang menghubungkan teluk Salerno dengan teluk Taranto.[1] Di kemudian hari, Italia diperluas hingga meliputi seluruh semenanjung Italia, serta kota Colonia Pietas Iulia (Pola) ...

For other uses, see Tank (disambiguation). Transit Authority of Northern KentuckyTANK BRT 881 at CVGParentGreenlineFounded1973[1]Headquarters3375 Madison PikeFort Wright, Kentucky[1]LocaleNorthern KentuckyService areaBoone, Kenton, Campbell Counties & Downtown CincinnatiService typebus service, paratransitAllianceSouthwest Ohio Regional Transit AuthorityRoutes27[1]Stops1,269HubsFort Wright Hub, Florence HubStationsCovington Transit CenterFleet107 busesDaily ridersh...

French geologist and petrologist Ferdinand André Fouqué in 1883 Ferdinand André Fouqué (21 June 1828 – 7 March 1904) was a French geologist and petrologist. He was born at Mortain, in the Manche département. At the age of twenty-one he entered the École Normale Supérieure in Paris, and from 1853 to 1858 he held the appointment of keeper of the scientific collections. In 1877 he became professor of natural history in the chair of geology at the Collège de France,[1] in Paris,...

2020 single by Tori Kelly UnbotheredSingle by Tori Kellyfrom the EP Solitude ReleasedAugust 11, 2020 (2020-08-11)Recorded2020GenrePopLength3:23Label Capitol School Boy Songwriter(s) Chloe George Jorgen Odegard Micah Premnath Tori Kelly Producer(s)Jorgen OdegardTori Kelly singles chronology Running Outta Love (2020) Unbothered (2020) Let It Snow! (2020) Lyric videoUnbothered on YouTube Unbothered is a song by American singer Tori Kelly. The track was released as the second singl...

1989 spy novel written by Len Deighton This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Spy Line – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) Spy Line First edition cover (UK, Hutchinson)AuthorLen DeightonCountryUnited KingdomLanguageEnglishGenreSpy novelPub...

См. также: Королевский колледж Колумбийский университетColumbia University Девиз лат. In lumine tuo videbimus lumen («Во свете твоём увидим свет») Основан 1754 Тип частный Целевой фонд $ 13,3 млрд Президент Ли Боллинджер Место расположения Нью-Йорк, штат Нью-Йорк, США 40°48′31″ с. ш. 73°57′44″ ...

Canadian journalist This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may rely excessively on sources too closely associated with the subject, potentially preventing the article from being verifiable and neutral. Please help improve it by replacing them with more appropriate citations to reliable, independent, third-party sources. (July 2021) (Learn how and when to remove this ...
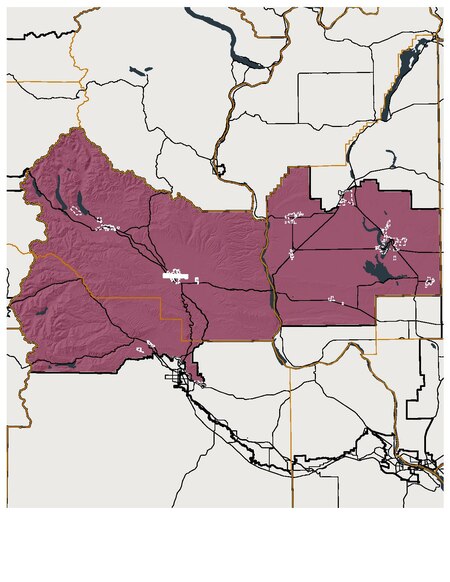
Washington's 13th legislative district map Washington's 13th legislative district is one of forty-nine districts in Washington state for representation in the state legislature. The district includes all or most of Lincoln, Grant, and Kittitas counties.[1] This rural district is represented by state senator Judy Warnick and state representatives Tom Dent (position 1) and Alex Ybarra (position 2), all Republicans.[2] See also Washington Redistricting Commission Washington State...

Swiss historian This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (January 2017) Emidio Campi (born 30 September 1943) is a Swiss historian. As a church historian, he is a specialist in the Reformation in Italy and Switzerland, and has researched and published articles on John Calvin, Peter Martyr Vermigli, Huldrich Zwingli, Heinrich Bullinger and other reformers.[1] Life He wa...

Stefano Bordon Bordon (a destra) durante la finale-scudetto del 1988-89 Dati biografici Paese Italia Altezza 183 cm Peso 95 kg Rugby a 15 Ruolo Tre quarti centro Ritirato 2003 Carriera Attività di club[1] 1985-1995 Rovigo1995-1996 Piacenza14 (0)1997-1998 Tolone2 (0)1998-2000 Rovigo2000-2003 CUS Verona Attività da giocatore internazionale 1990-1997 Italia29 (5) Attività da allenatore 2003-2004 CUS Verona2004-2005 Modena2005-2006 Colorno2005-2007...

Faneca-menor Estado de conservaciónPreocupación menor (UICN 3.1)[1]TaxonomíaReino: AnimaliaFilo: ChordataClase: ActinopterygiiSubclase: NeopterygiiInfraclase: TeleosteiSuperorden: ParacanthopterygiiOrden: GadiformesFamilia: GadidaeGénero: TrisopterusEspecie: T. minutusLinnaeus, 1758Distribución Distribución por Atlántico y MediterráneoSinonimia Gadus minutus (Linnaeus, 1758) Gadus capelanus (Lacepède, 1800) [editar datos en Wikidata] La faneca menor, cape...










