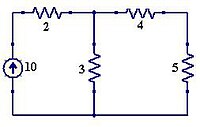
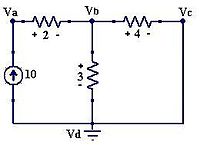
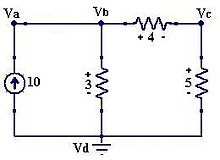
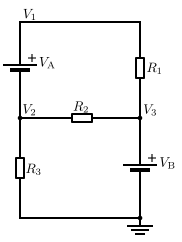
Análisis de nodos
|
Read other articles:
Hiệp hội bóng đá LibanAFCThành lập1933Trụ sởBeirutGia nhập FIFA1936Gia nhập AFC1964Chủ tịchHachem HaidarWebsitehttps://the-lfa.com.lb/ Hiệp hội bóng đá Liban (FLFA) (tiếng Ả Rập: الاتحاد اللبناني لكرة القدم; tiếng Pháp: Fédération libanaise de football) là tổ chức quản lý, điều hành các hoạt động bóng đá ở Liban. FLFA quản lý đội tuyển bóng đá quốc gia Liban, tổ chức các giải bóng

Invasi Soviet ke XinjiangBagian dari Pemberontakan KumulTanggalJanuari–April 1934LokasiXinjiangHasil Gencatan senjataPerubahanwilayah Xinjiang terbagi duaPihak terlibat Republik Tiongkok Uni Soviet Pasukan Rusia Putih Mongolia TorghutTokoh dan pemimpin Chiang Kai-shek Ma Zhongying Zhang Peiyuan † Ma Hushan Ma Shih-ming Joseph Stalin Jenderal Volgin Ishaq Beg Jenderal Bektieieff (Jenderal Bekteev) Kolonel ProshkukarovKekuatan Divisi ke-36 (Tentara Revolusioner Nasional) b...

ОлакурHolacourt Країна Франція Регіон Гранд-Ест Департамент Мозель Округ Форбак-Буле-Мозель Кантон Фолькемон Код INSEE 57328 Поштові індекси 57380 Координати 48°58′22″ пн. ш. 6°30′50″ сх. д.H G O Висота 228 - 262 м.н.р.м. Площа 2,92 км² Населення 90 (01-2020[1]) Густота 23,63 ос./

Order of algae For the order of silicoflagellates, see Dictyochales. Dictyotales Dictyota dichotoma Scientific classification Domain: Eukaryota Clade: Diaphoretickes Clade: SAR Clade: Stramenopiles Phylum: Gyrista Subphylum: Ochrophytina Class: Phaeophyceae Order: DictyotalesBory de Saint-Vincent, 1828 Family: DictyotaceaeLamouroux ex Dumortier, 1822 Genera[1] 21 genera Synonyms[1] ScoresbyellaceaeWomersley, 1987 Dictyotales (from Greek diktyotos 'netlike')[2...

Species of bird This article is about the bird species similar in appearance to ring-necked doves. For other uses, see Ring dove (disambiguation). Red collared dove Male in Singapore Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Columbiformes Family: Columbidae Genus: Streptopelia Species: S. tranquebarica Binomial name Streptopelia tranquebarica(Hermann, 1804) The red collare...

Chilla KianaLahirClara priscilia30 September 1995 (umur 28)Surabaya, Jawa Timur, IndonesiaKebangsaanIndonesiaNama lainChilla KianaPekerjaanPenyanyiMusisiAktrisPresenterTahun aktif2014–sekarangKarier musikGenreR&B, popInstrumenVokal, Piano, DrumLabelUniversal Music Indonesia Chilla Kiana (lahir 30 September 1995) adalah seorang penyanyi Indonesia. Dia terkenal saat menjadi pengisi suara Princess Elena di serial Disney, Elena of Avalor dan pengisi suara Maika Chōno di seri...

2022 Men's Softball World ChampionshipTournament detailsHost country New ZealandDates 26 November – 4 December 2022 Teams12Venue1 (in 1 host city)Final positionsChampions Australia (2nd title)Runner-up CanadaThird place United StatesFourth place ArgentinaTournament statisticsGames played50Attendance18,055 (361 per game)← 2019 Prague 2025 → Last updated on complete The 2022 WBSC Men's Softball World Championship was the 17th Men's Softball W...

Dewan Perwakilan Rakyat Daerah Kabupaten SolokDewan Perwakilan Rakyat Kabupaten Solok 2019-2024JenisJenisUnikameral Jangka waktu5 tahunSejarahSesi baru dimulai13 Agustus 2019PimpinanKetuaDodi Hendra (Gerindra) sejak 13 Januari 2021 Wakil Ketua IIvoni Munir, S.Farm.Apt. (PAN) sejak 30 Maret 2021 Wakil Ketua IILucki Efendi (Demokrat) sejak 20 September 2019 KomposisiAnggota35Partai & kursi PDI-P (2) NasDem (4) Hanura (2) Demokrat (...

Geographic boundary between northern and southern ChinaChina in the 12th century. The north of the Qinling–Huaihe Line was under control of the Jin dynasty, while the south was under control of the Song dynasty The Qinling–Huaihe Line (Chinese: 秦岭淮河线; pinyin: Qínlǐng Huáihé Xiàn) is a reference line used by geographers to distinguish between northern and southern China, corresponding roughly to the 33rd parallel.[1][2] Qinling refers to the Qin Mount...

Sacred cantata by Johann Sebastian Bach 1723 Preise, Jerusalem, den HerrnBWV 119Sacred cantata by J. S. BachNikolaikirche, LeipzigOccasionRatswechselPerformed30 August 1723 (1723-08-30): LeipzigMovements9VocalSATBInstrumentaltrumpetstimpanirecordersoboesstrings Preise, Jerusalem, den Herrn (Praise the Lord, Jerusalem),[1] BWV 119,[a] is a sacred cantata by Johann Sebastian Bach. He composed it in Leipzig for Ratswechsel, the inauguration of a new town counc...

Radio station in Roanoke, AlabamaWLWERoanoke, AlabamaFrequency1360 kHzBrandingEagle Sports 1360ProgrammingFormatSportsAffiliationsCBS Sports RadioOwnershipOwnerEagle's Nest, Inc.Sister stationsWELR-FM, WLAGHistoryFirst air dateMarch 10, 1950 (as WELR)[1]Former call signsWELR (1950-2013)Technical informationFacility ID18134ClassDPower1,000 watts (day)54 watts (night)Transmitter coordinates33°09′45″N 85°22′30″W / 33.16250°N 85.37500°W / 33.16250; -85....

American insurance company This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Westfield Insurance – news · newspapers · books · scholar · JSTOR (January 2013)...

Cathedral of the Roman Catholic Diocese of Sandhurst, Australia Church in AustraliaSacred Heart CathedralSacred Heart Cathedral36°45′36″S 144°16′26″E / 36.760°S 144.274°E / -36.760; 144.274Address80 Wattle Street, Bendigo, VictoriaCountryAustraliaDenominationRoman CatholicWebsitesacredheartcathedral.org.auHistoryStatusCathedral[1]Founded1895Founder(s)Martin CraneDedicationMost Sacred Heart of JesusConsecrated1901ArchitectureFunctional statusActiveAr...

СелоРошни-Чучечен. Роьшни-Чу 43°05′20″ с. ш. 45°27′27″ в. д.HGЯO Страна Россия Субъект Федерации Чечня Муниципальный район Урус-Мартановский Сельское поселение Рошни-Чуйское Глава Исаков Хусаин Мумаевич История и география Прежние названия до 1944 — Рошни-Чудо 1958 ...

class=notpageimage| Location in Alaska Ulak Island (Aleut: Yuulax̂[1]) is an island in the Delarof Islands subgroup of the Andreanof Islands in the Aleutian Islands chain of Alaska. Ulak is roughly 4 miles (6.4 kilometres) northeast of Amatignak Island. NASA picture of Ulak Island. References ^ Bergsland, K. (1994). Aleut Dictionary. Fairbanks: Alaska Native Language Center. External links B. A. Drummond, B. A. und A. L. Larned: Biological monitoring in the central Aleutian Islands, ...

City in Wisconsin, United StatesLoyal, WisconsinCityLooking north in downtown Loyal on WIS 98Location of Loyal in Clark County, Wisconsin.Coordinates: 44°44′15″N 90°29′48″W / 44.73750°N 90.49667°W / 44.73750; -90.49667Country United StatesState WisconsinCountyClarkArea[1] • Total1.37 sq mi (3.54 km2) • Land1.37 sq mi (3.54 km2) • Water0.00 sq mi (0.00 km2)Elev...

Battle of the Third Crusade This article is about the battle during the Third Crusade. For the battle during the First World War, see Battle of Jaffa (1917). Battle of JaffaPart of the Third CrusadeDate8 August 1192 (the conflict at Jaffa extended from 27 July to 8 August)LocationJaffa, Kingdom of JerusalemResult Crusader victoryBelligerents Angevin Empire Republic of GenoaRepublic of Pisa AyyubidsCommanders and leaders Richard I, King of England Saladin, Sultan of Egypt and SyriaStrength An ...

Austrian actress This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Käthe Gold – news · newspapers · books · scholar · JSTOR (January 2013) (Learn how and when to remove this template message) Käthe Gold as a cleaning lady in an episode of Der Kommissar (1974) Käthe Gold (11 February 1907 – 11 October 1997...

Human settlement in EnglandEllerdineEllerdine village hallEllerdineLocation within ShropshireOS grid referenceSJ608207Civil parishErcall MagnaUnitary authorityTelford and WrekinCeremonial countyShropshireRegionWest MidlandsCountryEnglandSovereign stateUnited KingdomPost townTELFORDPostcode districtTF6Dialling code01952PoliceWest MerciaFireShropshireAmbulanceWest Midlands UK ParliamentThe Wrekin List of places UK England Shropshire 52°46′59″N 2°34�...

Patung-patung di Rumah Kleopatra di Delos, Yunani Pakaian di Yunani kuno biasanya terdiri dari chiton, peplos, himation, dan chlamys. Pria dan wanita Yunani Kuno biasanya mengenakan sepasang pakaian yang dipakai di badan: sebuah pakaian dalam (chiton atau peplos) dan sebuah pakaian luar (himation atau chlamys).[1] Referensi ^ Alden, Maureen (January 2003), Ancient Greek Dress, Costume, 37.1: 1–16 Pranala luar Wikimedia Commons memiliki media mengenai Costume in ancient Greece....