Adición (matemática)
|
Read other articles:

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يونيو 2022) باي ديبي فال معلومات شخصية الميلاد 20 أبريل 1985 (العمر 38 سنة)تييس [لغات أخرى] الطول 1.86 م (6 قدم 1 بوصة) مركز اللعب مهاجم الجنسية السنغال الو

Calling / BreathlessLagu oleh Arashidari album LoveDirilis06 Maret 2013 (2013-03-06)FormatCD, CD + DVDDirekam2013GenrePopLabelJ StormKronologi singel Your Eyes (2012) Calling / Breathless (2013) Endless Game (2013) Calling / Breathless adalah single ke-40 boyband Jepang Arashi. Single ini dirilis di bawah label rekaman J Storm pada tanggal 6 Maret 2013. Calling digunakan sebagai lagu tema untuk drama Last Hope yang dibintangi oleh member Arashi, Masaki Aiba. Breathless digunakan sebagai ...

Dalam nama Tionghoa ini, nama keluarganya adalah Hua. Alex Hua TianAlex Hua TianPersonal informationKebangsaan TiongkokKategoriEventingLahir25 Oktober 1989 (umur 34)London Rekam medali Pesta Olahraga Asia 2014 Incheon Eventing tunggal 2018 Jakarta-Palembang Eventing tunggal Alex Hua Tian (Hanzi sederhana: 华天; Hanzi tradisional: 華天; Pinyin: Huà Tiān; Jyutping: Waa4 Tin1; lahir 25 Oktober 1989)[1] adalah seorang atlet balap kuda yang berkompetisi dala...

Pengkhotbah 8Lima Gulungan (Megilloth) lengkap pada Kodeks Leningrad (1008 Masehi), dengan urutan: Rut, Kidung Agung, Pengkhotbah, Ratapan dan Ester.KitabKitab PengkhotbahKategoriKetuvimBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen21← pasal 7 pasal 9 → Pengkhotbah 8 (disingkat Pkh 8) adalah pasal kedelapan Kitab Pengkhotbah dalam Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen. Secara tradisional diyakini digubah oleh raja Salomo, putra raja Daud.[1]...

Rural municipality in Saskatchewan, Canada See also: Marriott (disambiguation) Rural municipality in Saskatchewan, CanadaMarriott No. 317Rural municipalityRural Municipality of Marriott No. 317Location of the RM of Marriott No. 317 in SaskatchewanCoordinates: 51°45′04″N 107°55′05″W / 51.751°N 107.918°W / 51.751; -107.918[1]CountryCanadaProvinceSaskatchewanCensus division12SARM division6Formed[2]December 12, 1910Government[3] •...

Keuskupan Agung TarantoArchidioecesis TarentinaKatolik Katedral TarantoLokasiNegaraItaliaProvinsi gerejawiTarantoStatistikLuas1.056 km2 (408 sq mi)Populasi- Total- Katolik(per 2014)412.500415,500 (perkiraan) (99.3%)Paroki88Imam155 (diosesan)65 (Ordo Relijius)InformasiDenominasiGereja KatolikRitusRitus RomaPendirianAbad ke-6KatedralBasilica Cattedrale di S. CataldoKepemimpinan kiniPausFransiskusUskup AgungFilippo SantoroEmeritusBenigno Luigi Papa, O.F.M. Cap....

Railway station in Paris, France Musée d'OrsayRER stationPlatformsGeneral informationLocation7, Quai Anatole-France7th arrondissement of Paris, 75007FranceCoordinates48°51′37″N 2°19′31″E / 48.86028°N 2.32528°E / 48.86028; 2.32528Elevation27 m (89 ft)Owned bySNCFOperated bySNCFLine(s) RER CBus routes : 68, 69, 73, 84, 87, 94, Tootbus Paris : N01 Bus operatorsRATP, NoctilienConstructionStructure typeUndergroundOther informationStation c...

1937 film Madelon's DaughterDirected byGeorges PalluWritten byÉtienne Arnaud Francis Didelot André HeuzéProduced byMaurice de Roock Jean MugeliStarringHenri Garat Hélène Robert Ninon VallinCinematographyHugo S. DelattreMusic byJane Bos Louis Bousquet Marius-François GaillardProductioncompanyFilms de KosterDistributed byPathé Consortium CinémaRelease date13 October 1937Running time88 minutesCountryFranceLanguageFrench Madelon's Daughter (French: La fille de la Madelon) is a 1937 French...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Chinese folk art – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) Paper cutting for a Year of the Dog celebration. Chinese folk art or Chinese handcrafts are artistic forms inherited from a regio...

Chinese automobile Motor vehicle Chery Arrizo GXOverviewManufacturerCheryAlso calledChery Arrizo 6Chery Arrizo 5 Plus (facelift)Fownix Arrizo 6 Pro (facelift, Middle East)Omoda S5 (Russia and Kazakhstan)Omoda O5 (Mexico)[1]Production2018–2021 (as Arrizo GX) 2021-present (as Arrizo Plus) 2022-present (as Arrizo GT))AssemblyChina: Wuhu, AnhuiBrazil: Jacareí (Caoa Chery)Iran: Bam, Kerman (MVM)Body and chassisClassCompact car (C)Body style4-door sedanLayoutFront-engine, front...

Canadian animated series Top WingGenreChildren's adventureComedyCreated byMatthew FernandesDeveloped byScott KraftDirected byBill SpeersVoices ofTristan MercadoJonah WinebergLilly BartlamAbigail OliverLucas KalechsteinEthan PugiottoKingsley MarshalColin DoyleBryn McAuleyRaven DaudaScott LawJoseph MotikiCory DoranStacey DePassTal BachmanJulie SypeChristian DistefanoLacey-Lee EvinMili PatelTyler BarishFreddie HowsonComposersSteve D'AngeloTerry TompkinsLorenzo CastelliCraig McConnellJustin Forsl...

Frontera entre Afganistán y Pakistán Localización de Afganistán (naranja) y Pakistán (verde). La Línea Durand, que marca la frontera afgano-pakistaní. Afganistán Afganistán Pakistán Pakistán Longitud total 2670 kmParticularidades La frontera más larga de AfganistánHistoriaCreación 1893[editar datos en Wikidata] La frontera entre Afganistán y Pakistán es el lindero que separa los territorios del Emirato Islámico de Afganistán y de la República Islámica d...

У этого термина существуют и другие значения, см. Редколесье (значения). Редколесье в Питтсбурге, Пенсильвания, США Бельянские Татры, Словакия Редколе́сье — тип леса, характеризующийся относительно невысокой плотностью деревьев, отстоящих друг от друга на заметном уд...

Protein family This article is about the protein family. For other uses of Granin, see Granin (disambiguation). Granin (chromogranin or secretogranin)Structure of SS-cyclized catestatin fragment from chromogranin A.[1]IdentifiersSymbolGraninPfamPF01271InterProIPR001990PROSITEPDOC00365SCOP21cfk / SCOPe / SUPFAMOPM superfamily282OPM protein1lv4Available protein structures:Pfam structures / ECOD PDBRCSB PDB; PDBe; PDBjPDBsumstructure summary Granin (chromogranin and secretogr...

Rural district in Bushehr province, Iran For the village, see Chah Kutah. Rural District in Bushehr, IranChah Kutah Rural District Persian: دهستان چاهکوتاهRural DistrictChah Kutah Rural DistrictCoordinates: 29°09′17″N 51°03′03″E / 29.15472°N 51.05083°E / 29.15472; 51.05083[1]Country IranProvinceBushehrCountyBushehrDistrictChoghadakCapitalChah KutahTime zoneUTC+3:30 (IRST) Chah Kutah Rural District (Persian: دهستا...

Cet article est une ébauche concernant une unité ou formation militaire française. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. 76e régiment d'infanterie de ligne Insigne régimentaire du 76e régiment d'infanterie Création 1854 Dissolution Aout 1988 Pays France Branche Armée de terre Type Régiment d'infanterie Rôle Infanterie Devise Fortiter resistendo Inscriptionssur l’emblème Ulm 1805Iéna 1...

American government official and business advocate (born 1970) Isabel Guzman27th Administrator of the Small Business AdministrationIncumbentAssumed office March 17, 2021PresidentJoe BidenDeputyDilawar SyedPreceded byJovita Carranza Personal detailsBorn1970 or 1971 (age 52–53)[1]Burbank, California, U.S.EducationUniversity of Pennsylvania (BS) Isabella Casillas Guzman[2] (born 1970) is an American government official serving as the administrator of the Sm...

Peta infrastruktur dan tata guna lahan di Komune La Meyze. = Kawasan perkotaan = Lahan subur = Padang rumput = Lahan pertanaman campuran = Hutan = Vegetasi perdu = Lahan basah = Anak sungaiLa Meyze merupakan sebuah komune di departemen Haute-Vienne di Prancis. Lihat pula Komune di departemen Haute-Vienne Referensi INSEE lbsKomune di departemen Haute-Vienne Aixe-sur-Vienne Ambazac Arnac-la-Poste Augne Aureil Azat-le-Ris Balledent La Bazeuge Beaum...

UNESCO World Heritage Site in Kantō region, Japan Shrines and Temples of NikkoUNESCO World Heritage SiteLocationNikkō, Tochigi Prefecture, Kantō region, JapanCriteriaCultural: (i), (iv), (vi)Reference913Inscription1999 (23rd Session)Area50.8 ha (126 acres)Buffer zone373.2 ha (922 acres)Coordinates36°45′23″N 139°35′58″E / 36.7565°N 139.5994°E / 36.7565; 139.5994 The UNESCO World Heritage Site Shrines and Temples of Nikkō encompasses 1...
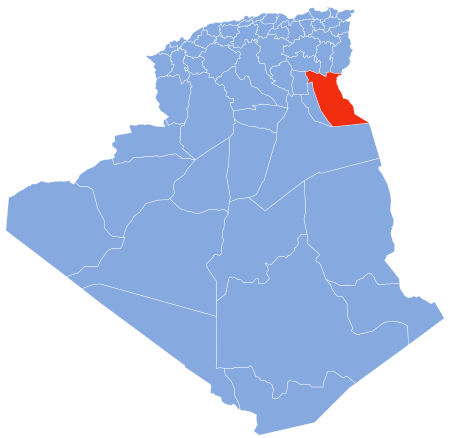
Commune and town in El M'Ghair Province, AlgeriaEl M'Ghair اﻟﻤﻐﻴﺮCommune and townLocation of El M'Ghair commune within El M'Ghair ProvinceEl M'GhairLocation of El M'Ghair within AlgeriaCoordinates: 33°57′2″N 5°55′27″E / 33.95056°N 5.92417°E / 33.95056; 5.92417Country AlgeriaProvinceEl M'Ghair ProvinceDistrictEl M'Ghair DistrictElevation2 m (7 ft)Population (2008)[1] • Total49,793Time zoneUTC+1 (CET) El M'Gh...





































