En geometrio, pluredro de Waterman aŭ Waterman-a pluredro aŭ mallonge WP estas pluredro kreita per proksima pakigo de sferoj, forigo de sferoj kiuj estas pli malproksima de la centro ol certa radiuso, kaj kreo de konveksa koverto de centroj de la restintaj sferoj.
![]()
Kuba proksima pakigo de sferoj kun radiuso (2*24)1/2
|

Pluredro de Waterman W24 de fonto 1
|
Pluredroj de Waterman formas vastan familion de pluredroj. Iu de ilin havas multajn simetriojn aŭ regulajn geometriajn formojn. Iu alia estas nur aro de malregulaj konveksaj plurlateroj kiel edroj. La plej populara pluredroj de Waterman estas tiuj kun centroj en la punkto (0,0,0) kaj konstruitaj el centoj de plurlateroj. Tiaj pluredroj similas al grandaj sferoj. Fakte, ju pli multajn edrojn havas pluredro de Waterman, des pli ĝia formo similas al ĝia ĉirkaŭskribita sfero kaj ĝiaj volumeno kaj tuteca areo estas proksimaj al tiuj de la ĉirkaŭskribita sfero.
Kun ĉiu punkto de 3-spaco oni povas asociigi familion de pluredroj de Waterman kun malsamaj radiusoj de la ĉirkaŭskribitaj sferoj. Pro tio, oni povas konsideri pluredrojn de Waterman kiel 4D spaco W(x,y,z,r), kie x, y ,z estas koordinatoj de punkto en 3D, kaj r estas la radiuso, kaj r>1.
Sep fontoj de kuba proksima pakigo
Povas esti sep fontoj difinitaj en kuba proksima pakigo [1], kie n = 1, 2, 3, ...:
- Fonto 1: centro (0,0,0), radiuso (2*n)1/2
- Fonto 2: centro (1/2,1/2,0), radiuso (2+4*n)1/2/2
- Fonto 3: centro (1/3,1/3,2/3), radiuso (6*(n+1))1/2/3
- Fonto 3*: centro (1/3,1/3,1/3), radiuso (3+6*n)1/2/3
- Fonto 4: centro (1/2,1/2,1/2), radiuso (3+8*(n-1))1/2/2
- Fonto 5: centro (0,0,1/2), radiuso (1+4*n)1/2/2
- Fonto 6: centro (1,0,0), radiuso (1+2*(n-1))1/2
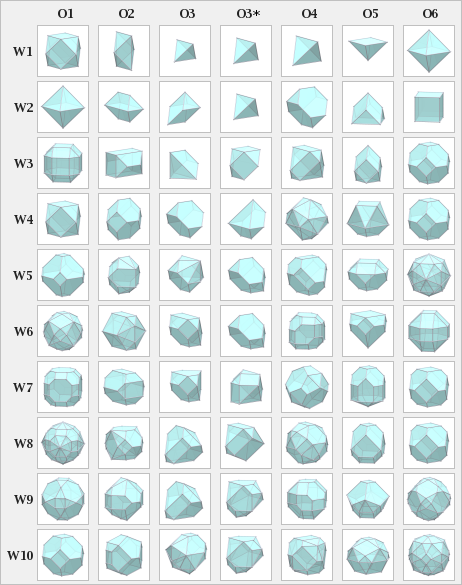
Platonaj kaj arĥimedaj solidoj kiel pluredroj de Waterman
Iuj pluredroj de Waterman estas platonaj solidoj kaj arĥimedaj solidoj. Por ĉi tiu komparo de pluredroj de Waterman ili estas ununormigitaj, ekzemple W2 O1 havas malsaman volumenon ol W1 O6, sed ili havas la saman formon.
Platonaj solidoj
Arĥimedaj solidoj
La aliaj ne havas ĉi tian prezenton.
Ekzistas pluredroj de Waterman kun du diversaj lateraj longoj kiuj pro tio ne estas arĥimedaj solidoj, sed estas topologie ekvivalentaj al ili:
Ĝeneraligitaj pluredroj de Waterman
Ĝeneraligitaj pluredroj de Waterman estas difinita kiel la konveksa koverto derivita de la punkta aro de iu sfera parto de iu regula krado.
Estas pristuditaj jenaj 10 kradoj:
_bcc_, kubokedro, diamanto, _fcc_, _hcp_, senpintigita okedro, romba dekduedro, simpla kuba, senpintigita kvaredro kvaredro, senpintigita kvaredro senpintigita okedra kubokedro.
Ĉiu el la 10 kradoj estis ekzamenita por trovi tiujn fontajn punktojn kiuj donas unikajn pluredrojn kaj ankaŭ posedas iun minimuman simetrion.
En ĉiu krado ekzistas malfinia serio de pluredroj.
Eksteraj ligiloj