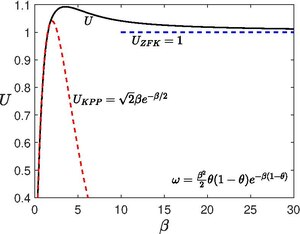
ZFK equation
|
Read other articles:

花嫁衣裳は誰が着るジャンル テレビドラマ原作 細川智栄子「あこがれ」企画 春日千春、重村一脚本 長野洋、林さわこ、佐々木守監督 土屋統吾郎、岡本弘、竹本弘一、米山紳出演者 堀ちえみ伊藤かずえ松村雄基原知佐子梶芽衣子名古屋章織本順吉初井言榮 ほかオープニング 椎名恵「愛は眠らない」エンディング 同上製作プロデューサー 柳田博美、千原博司(大映テレ

U.S. government position United StatesAssistant Secretary of Statefor International Security and NonproliferationSeal of the United States Department of StateIncumbentC.S. Eliot Kangsince March 31, 2022Reports toUnder Secretary of State for Arms Control and International Security AffairsNominatorPresident of the United StatesInaugural holderStephen Rademaker (acting)Formation2005Websitewww.state.gov/t/isn/index.htm The Assistant Secretary of State for International Security and Nonprolif...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. PT ICTSI Jasa Prima TbkJenisPublik (IDX: KARW)IndustrijasaDidirikan1978KantorpusatJakarta, IndonesiaTokohkunciRomeo Andres Salvador, Presiden DirekturProdukbongkar muatPendapatan USD 7,9 juta (2017) USD 6,32 juta (2018) Laba bersih USD 2,42 juta (2017...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2017) كازو موري (باليابانية: 森一生) معلومات شخصية الميلاد 15 يناير 1911 ماتسوياما، إهيمه تاريخ الوفاة 29 يونيو 1989 (78 سنة) الجنسية اليابان الحياة الع�...

Akademia Sztuki w SzczecinieAcademy of Art in Szczecin Pałac „Pod Globusem” w Szczecinie (2022) Data założenia 2010 Państwo Polska Województwo zachodniopomorskie Adres pl. Orła Białego 270-562 Szczecin Liczba studentów 760 Rektor dr hab. Mirosława Jarmołowicz Położenie na mapie SzczecinaAkademia Sztuki w Szczecinie Położenie na mapie PolskiAkademia Sztuki w Szczecinie Położenie na mapie województwa zachodniopomorskiegoAkademia Sztuki w Szczecinie 53°25′34,36

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2019) هاري لوران معلومات شخصية الميلاد 15 أبريل 1895 إقليم تاراناكي الوفاة 9 ديسمبر 1987 (92 سنة) هاستينجس، نيوزيلندا مواطنة نيوزيلندا الحياة العملية الم

Der Titel dieses Artikels ist mehrdeutig. Weitere Bedeutungen sind unter Verny (Begriffsklärung) aufgeführt. Verny Verny (Frankreich) Staat Frankreich Region Grand Est Département (Nr.) Moselle (57) Arrondissement Metz Kanton Faulquemont Gemeindeverband Sud Messin Koordinaten 49° 0′ N, 6° 12′ O49.0072222222226.2033333333333Koordinaten: 49° 0′ N, 6° 12′ O Höhe 172–246 m Fläche 3,9 km² Einwohner 1.981 (1. Januar 2020) Bevölk...

Artikel ini bukan mengenai Berakhah atau Berakhot (Talmud). Ulangan 32:50–33:29 dalam Kodeks Aleppo V'Zot HaBerachah, VeZos HaBerachah, VeZot Haberakha, V'Zeis Habrocho, V'Zaus Haberocho, V'Zois Haberuchu, atau Zos Habrocho (וְזֹאת הַבְּרָכָה – Ibrani untuk dan ini adalah berkat, kata-kata pertama dalam parsyah tersebut) adalah Bacaan Taurat Mingguan (פָּרָשָׁה, parashah) ke-54 dan terakhir dalam siklus bacaan Taurat Yahudi tahunan dan ke-11 dan terakhir dalam Kit...

History of New York City rapid transit (1899–1940) Brooklyn Union Elevated RailroadNew York Consolidated RailroadNew York Rapid Transit CorporationOverviewHeadquartersBrooklyn, NYLocaleNew York CityDates of operation1899 – 1907 (B'klyn Heights RR)1907 – 1912 (B'klyn Union El. RR)1912 – 1923 (NY Consol. RR)1923–1940 (NYRT Corp.)TechnicalTrack gauge4 ft 8+1⁄2 in (1,435 mm) standard gauge Starti...

Artikel ini bukan mengenai Miss Korea. Miss Grand KoreaLogo Miss GrandTanggal pendirian2017TipeKontes kecantikanKantor pusatSeoulLokasi Korea SelatanJumlah anggota Miss Grand InternationalBahasa resmi KoreaPresidenKim Ho-seongSitus webwww.missgrandkorea.co.kr Park Serim, Miss Grand Korea 2019 Miss Grand Korea (bahasa Korea: 미스 그랜드 코리아) adalah kontes kecantikan di Korea Selatan yang diselenggarakan sejak tahun 2017 oleh 1L2H company yang diketuai oleh seorang pengusaha...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (يوليو 2019) منتخب إيران تحت 23 سنة لكرة الطائرة للرجال كونفدرالية الاتحاد الآسيوي لكرة الطائ

Species of fish Finless sole Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Actinopterygii Order: Pleuronectiformes Family: Soleidae Genus: Pardachirus Species: P. marmoratus Binomial name Pardachirus marmoratus(Lacépède, 1802) Synonyms Achirus marmoratus Lacepède, 1802 Achirus barbatus Lacepède, 1802 Achirus punctatus Desjardins, 1837 Pardachirus marmoratus, the finless sole, speckled sole or Red Sea Moses sole,[1] is a species of flatf...

301st Maneuver Enhancement BrigadeGroup insigniaActive2008-Country United StatesBranchUnited States Army ReserveSizeBrigadePart of416th Theater Engineer CommandHeadquartersJoint Base Lewis-McChord, WashingtonMilitary unit 301st Maneuver Enhancement Brigade is a United States Army Reserve unit based in Joint Base Lewis-McChord, Washington. The Maneuver Enhancement Brigade is a brigade size headquarters with a modular organization that is designed to provide support to the combatant c...

此條目没有列出任何参考或来源。 (2020年5月7日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以改善这篇条目。无法查证的內容可能會因為異議提出而被移除。 奥得河畔科斯琴Kostrzyn nad OdrąKüstrin an der Oder城市 旗幟徽章奥得河畔科斯琴奥得河畔科斯琴在波蘭的位置坐标:52°35′18″N 14°40′00″E / 52.58833°N 14.66667°E / 52.58833; 14.66667坐标:52°35′1...

Ken Watanabe Ken Watanabe (渡辺 謙code: ja is deprecated , Watanabe Ken, lahir 21 Oktober 1959) adalah seorang pemeran berkebangsaan Jepang yang memenangkan nominasi Academy Award. Dia berkarier di dunia film sejak tahun 1984. Filmografi Film Tahun Judul Peran Catatan 1984 MacArthur's Children Tetsuo Nakai 1985 Kekkon Annai Mystery Funayama Tetsuya / Masakazu Sekine Tampopo Gun 1986 The Sea and Poison Toda 1998 Welcome Back, Mr. McDonald Raita Onuki, sopir truk Kizuna Detective Sako Akio 2...

يوسف وزينب الصنف دراما الموضوع بعد فشل علاقة حب يوسف من زميلته أميرة يقرر السفر للعمل في جزيرة مالديف حيث يقع في حب فتاة هندية هناك تاريخ الصدور يناير 1984 مدة العرض 117 دقيقة البلد مالديف - مصر اللغة الأصلية اللغة العربية (اللهجة المصرية) اللغة الديفيهية (لغة أهل مالديف) مواقع �...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (January 2016) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Surya Sen Park – news · newspapers · books · scholar · JSTOR (July 2013) (Learn how and...

Island in Chile Aracena IslandNative name: Isla AracenaAracena Island, at the Strait of MagellanGeographyCoordinates54°10′S 71°20′W / 54.167°S 71.333°W / -54.167; -71.333Area1,164 km2 (449 sq mi)Coastline457 km (284 mi)Highest elevation1,158 m (3799 ft)Highest pointMonte Vernal[1]AdministrationChileRegionMagallanes RegionProvinceMagallanes ProvinceCommunes of ChilePunta ArenasAdditional informationNGA UFI -87...

English churchman Ridgeway as Bishop of Chichester Charles John Ridgeway (14 July 1841 – 28 February 1927) was an English churchman, the Bishop of Chichester from 1908 to 1919.[1] Life Ridgeway was born into an ecclesiastical family: his father Joseph Ridgeway was Vicar of Christ Church, Tunbridge Wells;[2] his younger brother of Frederick became Bishop of Salisbury. He was educated at St Paul's School, and matriculated in 1860 at Trinity College, Cambridge, gra...

American actress and former model Alana StewartStewart in 2023BornAlana Kaye Collins (1945-05-18) May 18, 1945 (age 78)San Diego, California, U.S.Other namesAlana Collins-HamiltonAlana HamiltonOccupation(s)Actress, model, producer, authorSpouses George Hamilton (m. 1972; div. 1975) Rod Stewart (m. 1979; div. 1984) ChildrenAshley HamiltonKimberly StewartSean StewartModeling informa...



![{\displaystyle \theta \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fead1e7dceab4be5ab2e91f5108144722daa8c36)