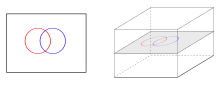
Transversality (mathematics)
|
Read other articles:

Nicole Trunfio Información personalNacimiento 16 de marzo de 1986 (37 años)Merredin (Australia) Nacionalidad Australiana e italianaCaracterísticas físicasAltura 1,78 m Ojos Avellana Cabello Castaño FamiliaCónyuge Gary Clark Jr. (matr. 2016)Hijos 3EducaciónEducada en Australind Senior High School Información profesionalOcupación Modelo y actriz Sitio web www.nicoletrunfio.net [editar datos en Wikidata]Nicole Trunfio (16 de marzo de 1986) es una modelo, y actriz...

U-class destroyer converted to Type 15 frigate of the Royal Navy For other ships with the same name, see HMS Ulster. HMS Ulster on the River Tyne, 26 June 1943 History United Kingdom NameHMS Ulster BuilderSwan Hunter, Tyne and Wear, United Kingdom[1] Laid down12 November 1941 Launched9 November 1942 Commissioned30 June 1943 Decommissioned1977 IdentificationPennant number R83 FateWithdrawn from service 1977; Broken up 1980 General characteristics V-class destroyer Class and typeV-class...

Soul Eater: Battle ResonanceInformación generalDesarrollador Namco Bandai[1]Productor Namco BandaiDatos del juegoGénero LuchaModos de juego 1 - 2 jugadoresDatos del softwarePlataformas PS2PSPDatos del hardwareFormato DVD (PS2)UMD (PSP)DesarrolloLanzamiento 29 de enero 2009[2][editar datos en Wikidata] Soul Eater: Battle Resonance (ソウルイーター バトルレゾナンス, Sōru Ītā Batoru Rezonansu?) es un videojuego de lucha basado en el manga y anime Soul E...

Blurring technique in images or videos This article is about the graphical editing/censorship technique. For the undesirable phenomenon in which individual pixels are visible, see Pixelation. For the stop motion animation technique, see Pixilation. This article on image censorship needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this article on image censorship. Unsourced material may be challenged and removed.Find so...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أكتوبر 2021) عدم المساواة في الانتباه (بالإنجليزية: Attention inequality) هو مصطلح يستخدم لاستهداف عدم المساواة في توزيع الانتباه عبر المستخدمين على الشبكات الاجتماعية، والناس...

Men's moguls at the 2003 Asian Winter GamesVenueAjigasawa Ski AreaDates6 February 2003Competitors7 from 3 nationsMedalists Yu Masukawa Japan Kenro Shimoyama Japan Ivan Sidorov Kazakhstan2011 → Freestyle skiing at the2003 Asian Winter GamesMogulsmenwomenvte Main article: Freestyle skiing at the 2003 Asian Winter Games The men's moguls at the 2003 Asian Winter Games was held on 6 February 2003 at Ajigasawa Ski Ar...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: SMK Sultan Badlishah – news · newspapers · books · scholar · JSTOR (February 2018) (Learn how and when to remove this template message) Secondary school, cluster schoolSMK Sultan BadlishahAddressJalan Sultan Badlishah,09000 Kulim,Kedah, MalaysiaInformationForme...

Garden Corner Garden Corner is a Grade II* listed house at 13 Chelsea Embankment, Chelsea, London. It was built in 1879 in deep red brick in the Dutch Renaissance style on the site of the Old Swan pub, and the architect was Edward l'Anson Jr.[1][2] James Staats Forbes, the Scottish railway engineer, railway administrator and art collector lived there until his death there in 1904.[3] In 1906–07, the interior was substantially redesigned in the Arts and Crafts style b...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (نوفمبر 2023) هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر مغاير للذي أنشأها؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً ...

One-day cricket competition in the United Kingdom Friends Provident TrophyCountries EnglandAdministratorEngland and Wales Cricket BoardFormatList A cricketFirst edition1963Latest edition2009Number of teams20Current championHampshireMost successfulLancashire (7 titles) The Friends Provident Trophy was a one-day cricket competition in the United Kingdom. It was one of the four tournaments in which the eighteen first-class counties competed each season. They were joined by teams from Scotla...

Names of the Bus companies in the Philippines This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of bus companies of the Philippines – news · newspapers · books ...

For other ships with the same name, see HMS Hurworth. HMS Hurworth operating in the English Channel History United Kingdom NameHMS Hurworth OperatorRoyal Navy BuilderVosper Thornycroft Launched25 September 1984 Sponsored byLady Anne Hallifax,[2] wife of Admiral Sir David Hallifax KCB KCVO KBE Commissioned2 July 1985[1] HomeportHMNB Portsmouth, Hampshire Identification Pennant number: M39 IMO number: 8401509 MMSI number: 232002833 Callsign: GBPL Statusin active ser...

Maximum Power Principle in Energy Systems Language adapted from Odum and Odum 2000, p. 38 The maximum power principle or Lotka's principle[1] has been proposed as the fourth principle of energetics in open system thermodynamics, where an example of an open system is a biological cell. According to Howard T. Odum, The maximum power principle can be stated: During self-organization, system designs develop and prevail that maximize power intake, energy transformation, and those uses that...

Islas Sebaldes Jason Islands Mapa satelitalUbicación geográficaMar Océano AtlánticoContinente América del SurCoordenadas 51°04′37″S 60°58′08″O / -51.077, -60.969Ubicación administrativaPaís Reino Unido Reino Unido(reclamada por Argentina)División Islas Malvinas(De acuerdo a la Argentina, las islas forman parte de la provincia de Tierra del Fuego, Antártida e Islas del Atlántico Sur)Datos geográficosIslas 8 islas e islotes menoresMapa ...

Spanish autonomous agency You can help expand this article with text translated from the corresponding article in Spanish. (October 2021) Click [show] for important translation instructions. View a machine-translated version of the Spanish article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated ...

This article is about the defunct Greek airline. For other airlines with similar names, see Galaxy Air and Galaxy Airlines (disambiguation). Galaxy Airways was a Greek charter airline based in Athens that existed from 1999 to 2001. It had a fleet of 3 aircraft, one Boeing 737-500 and two Boeing 737-400.[1] History Galaxy Airways Boeing 737 1999 Company foundation year. Was founded by Capt. Theodore Kokmotos. Initial scheduled flights operation began immediately with a Boeing 737-500, ...

1914 novel by Edgar Rice Burroughs The Warlord of Mars The Warlord of MarsAuthorEdgar Rice BurroughsCountryUnited StatesLanguageEnglishSeriesBarsoomGenreScience fantasyPublisherA. C. McClurgPublication date1913-1914Media typePrint (hardback & paperback)Pages296Preceded byThe Gods of Mars Followed byThuvia, Maid of Mars The Warlord of Mars is a science fantasy novel by American writer Edgar Rice Burroughs, the third of his Barsoom series. Burroughs began writing i...

Class of historically related American English dialects For the generalized variety of English in North America, see North American English. Northern American EnglishNorthern U.S. EnglishRegionNorthern United StatesLanguage familyIndo-European GermanicWest GermanicIngvaeonicAnglo–FrisianAnglicEnglishNorth American EnglishAmerican EnglishNorthern American EnglishEarly formsOld English Middle English Early Modern English Language codesISO 639-3–Glottolognort331621st-century research unites ...

О регионе Украины в её международно признанных границах см. Донецкая область. Иное название этого понятия — «Донецкая республика»; см. также другие значения. Самопровозглашённое государственное образование (до 2022)Субъект Российской Федерации (c 2022)Донецкая Наро...

This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (June 2021) (Learn how and when to remove this template message) Dr. Noa Regev (born February 17, 1982) is an Israeli lecturer in film, CEO of the Israel Film Fund, and a former CEO of the Jerusalem Cinematheque.[1] Early life Noa Regev was born in Tel ...

























![{\displaystyle {\mathfrak {g}}=[{\mathfrak {g}},e]\oplus {\mathfrak {g}}_{f}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca3d22d9eb3814acfe1ee8f250b1537642974845)
![{\displaystyle [{\mathfrak {g}},e]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46f0f2646cff543757ce17c8a942253034595694)




