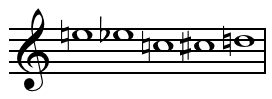Set (music)
|
Read other articles:

Para otros usos de este término, véase What's Going On (desambiguación). What's Going OnÁlbum de Marvin GayePublicación 21 de mayo de 1971Grabación Hitsville USA (Studio A)Golden World (Studio B)Hitsville Westjunio 1970 (What's Going On)marzo-abril 1971 (resto del álbum)Género(s) SoulDuración 35:28Discográfica Tamla TS 310Productor(es) Marvin GayeCalificaciones profesionales Allmusic link Robert Christgau (B+) link Rolling Stone 23 de enero de 2003 UNCUT mayo de 2003 Cronología...

Corps of the Union Army during the American Civil War This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: XXIV Corps Union Army – news · newspapers · books · scholar · JSTOR (September 2014) (Learn how and when to remove this template message) XXIV Corps was a corps of the Union Army during the American Civ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Wellesley, Massachusetts – news · newspapers · books · scholar · JSTOR (November 2021) (Learn how and when to remove this template message) Town in Massachusetts, United StatesWellesley, MassachusettsTownWellesley Town Hall SealLocation of Wellesley in Norfolk ...

Brazilian association football player (born 2000) In this Portuguese name, the first or maternal family name is Paixão and the second or paternal family name is de Oliveira. Júnior is a generational suffix used for someone whose name is the same as their father, like Jr. in English. Not to be confused with Carlos Vinícius. Vinícius Júnior Vinícius Júnior in 2021Personal informationFull name Vinícius José Paixão de Oliveira Júnior[1]Date of birth (2000-07-12) 12...

يعد الخاطف العشرين إرهابياً إضافياً محتملاً في هجمات 11 سبتمبر 2001 الذي لم يتمكن، لأي سبب من الأسباب، من المشاركة. ويقال إن الخاطف العشرين، وإن لم يكن حاضرا أثناء الهجمات الفعلية، قد شارك بعمق في الاستعدادات. كان هناك العديد من التغيرات في مخطط 9/11، حيث يتذبذب عدد الإرهابيين �...

Nota: Para o personagem dos X-Men Colossus, veja Colossus (Marvel Comics). Colossus Computador programável digital eletrônico para fins especiais Um computador Colossus sendo operado Desenvolvedor Tommy Flowers, assistido por Sidney Broadhurst, William Chandler e para as máquinas Mark 2, Allen Coombs Fabricante Post Office Research Station Comercializado 1943 Descontinuado 8 de Junho de 1945 Lançamento Mark I: Dezembro de 1943Mark II: 1 de Junho de 1944 Características Proces...

Takelesi (Douglas) Lagaluga JPBorn(1924-06-10)10 June 1924Avatele, NiueDied30 March 2009(2009-03-30) (aged 84)Niue Foou Hospital, NiueOccupation(s)Administrator, PoliticianSpouseIola Lohana Douglas (née Ikimotu) Takelesi (Douglas) Lagaluga. JP. (10 June 1924 – 30 March 2009) was a Niuean administrator, politician, and respected elder from the village of Avatele. Lagaluga served the Government of Niue for 40 years, first as a Clerk to the Resident Commissioner then redeployed to the is...

Jake Zyrus discographyStudio albums5Music videos8EPs3Singles15 The discography of Jake Zyrus, a Filipino singer, consists of five studio albums, three extended plays (EP), fifteen singles, and eight music videos. Jake recorded under the name Charice before coming out in 2017 as a transgender man. He was the first Asian solo artist to reach the top 10 of Billboard 200 chart.[1] Forbes listed him among the most influential singers in Asia.[2] Guinness World Records recognized hi...

此條目可参照英語維基百科相應條目来扩充。 (2021年12月25日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 系列条目反犹太主义犹太人历史及歧視的一部分 历史(英语:History of antisemitism) 年表(英语:Timeline of ant...

У Вікіпедії є статті про інші значення цього терміна: Бражники. село Бражники Країна Україна Область Харківська область Район Харківський район Громада Нововодолазька селищна громада Облікова картка Бражники Основні дані Населення 147 Площа 0,72 км² Густота насе...

LesznoRailway StationLeszno railway stationGeneral informationLocationLeszno, Greater Poland VoivodeshipPolandOperated byPKP Polskie Linie KolejoweLine(s)14: Łódź-Forst (Lausitz) railway 271: Wrocław–Poznań railway 359 Leszno–Zbąszyń railwayPlatforms8HistoryOpened1856; 167 years ago (1856)Rebuilt1899, 1971, 2012Services Preceding station Polregio Following station Lipno Nowetowards Poznań Główny PR Rydzynatowards Wrocław Główny Terminus Lasocicetowards Głog...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: As the World – news · newspapers · books · scholar · JSTOR (December 2021) (Learn how and when to remove this template message) 1995 studio album by EcholynAs the WorldStudio album by EcholynReleasedMarch 7, 1995RecordedFebruary–June 1994StudioWoodlan...

Nationality law of Madagascar Malagasy Nationality CodeParliament of Madagascar Long title Ordonnance No. 60-064 du 22 juillet 1960 portant Code de la nationalité malgache (modifiée par la Loi No. 1961-052; la Loi No.1962-005; l’ordonnance no.1973-049; la Loi No. 1995-021; et la Loi No. 2016-038.) Enacted byGovernment of MadagascarStatus: Current legislation Malagasy nationality law is regulated by the Constitution of Madagascar, as amended; the Malagasy Nationality Code, and its rev...

Part of a series onPsychology Outline History Subfields Basic psychology Abnormal Affective neuroscience Affective science Behavioral genetics Behavioral neuroscience Behaviorism Cognitive/Cognitivism Cognitive neuroscience Social Comparative Cross-cultural Cultural Developmental Differential Ecological Evolutionary Experimental Gestalt Intelligence Mathematical Moral Neuropsychology Perception Personality Positive Psycholinguistics Psychophysiology Quantitative Social Theoretical Applied psy...

English singer and actress (born 1981) Hannah SpearrittSpearritt in 2013BornHannah Louise Spearritt (1981-04-01) 1 April 1981 (age 42)Great Yarmouth, Norfolk, EnglandEducation Lynn Grove GM High School East Norfolk Sixth Form College OccupationsActresssingerYears active1993–presentPartnerAdam ThomasChildrenTaya Thomas Spearritt Tora Thomas SpearrittRelativesEddie Spearritt (uncle) Hannah Louise Spearritt (born 1 April 1981)[1] is an English actress and singer. She is an or...

Serbs in SFR Yugoslavia (excluding Serbs of Montenegro) in 1981 From August 1990 to November 1991, during the breakup of Yugoslavia, several Serb Autonomous Regions,[1][2] or Districts[3] (sing. Serbian: Српска аутономна област (САО) / Srpska autonomna oblast (SAO)) were proclaimed in the Yugoslav republics of SR Croatia and SR Bosnia and Herzegovina in light of the possible secession of the republics from the Socialist Federal Republic of Yugos...

حادثة إطلاق الحوثيين صاروخ باليستي باتجاه مكة المكرمة 2016 جزء من اعتراض الصواريخ البالستية في الحرب الأهلية اليمنية المعلومات الموقع منطقة مكة المكرمة السعودية التاريخ 27 محرم 1438 هـ28 أكتوبر 2016 الهدف مكة المكرمة (بحسب التحالف العربي بقيادة السعودية) مطار جدة (بحسب الحوثي...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Arthur Henry GoodenLahir23 Oktober 1879Inggris, Britania RayaMeninggal22 Juli 1971Los Angeles, California, Amerika SerikatPekerjaanPenulis naskahTahun aktif1916-1937 Arthur Henry Gooden (23 Oktober 1879 – 22 Juli 1971) adalah seor...

Mexican singer, songwriter, actor, and television host For other people named Pedro Fernández, see Pedro Fernández. Pedro FernándezBackground informationBirth nameJosé Martín CobosAlso known as Pedrito Fernández Born (1969-09-28) September 28, 1969 (age 54)Guadalajara, Jalisco, MexicoOriginMexícoGenresRegional Mexican, Latin popOccupations Singer actor songwriter composer producer TV host Instruments Vocals guitar piano Years active1976–presentWebsitePedro Fernández OficialMusi...

1957 novel by A.E. van Vogt Cover of the first edition, published by Simon & Schuster. Art by H. Marcelin. The Mind Cage is a 1957 science fiction novel by Canadian-American writer A. E. Van Vogt, adapted from the short story The Great Judge (1948). Plot summary David Marin risks his career to defend Wade Trask, a scientist being tried for sedition, but when Trask switches their brains, Marin finds himself branded an enemy of the state. Reception Floyd C. Gale wrote that Van Vogt, master ...