Philo line
|
Read other articles:

Indigenous folk dance from Assam, India Bihu danceYouths perform Bihu dance in AssamGenreFolk danceOriginAssam, India The Bihu dance is an indigenous folk dance from the Indian state of Assam related to the Bihu festival and an important part of Assamese culture. Performed in a group, the Bihu dancers are usually young men and women, and the dancing style is characterized by brisk steps, and rapid hand movements. The traditional costume of dancers is colorful and centered round the red color ...

No debe confundirse con Monumento a Colón. Monumento a Colón Vista del monumento antes de ser retirado.LocalizaciónPaís MéxicoLocalidad Ciudad de México, MéxicoCoordenadas 19°25′59″N 99°09′17″O / 19.433083333333, -99.15475HistoriaConstrucción 1873-1877Inauguración 1877Demolición 2021Autor Charles Cordier.Arquitecto Charles CordierDedicado a Cristóbal ColónCaracterísticasEstilo NeoclásicoProtecciónCaracterísticas La segunda glorieta del Paseo de ...

1973 essay by Theodosius Dobzhansky Mosaic medallion in the floor of the main hall of the Jordan Hall of Science, University of Notre Dame. Nothing in Biology Makes Sense Except in the Light of Evolution is a 1973 essay by the evolutionary biologist Theodosius Dobzhansky, criticising anti-evolution creationism and espousing theistic evolution. The essay was first published in American Biology Teacher in 1973.[1] Dobzhansky first used the title statement, in a slight variation, in a 19...

У Вікіпедії є статті про інші географічні об’єкти з назвою Акрон. Місто Акронангл. Akron Координати 42°49′31″ пн. ш. 96°33′24″ зх. д. / 42.82527777780577338° пн. ш. 96.55666666669478104° зх. д. / 42.82527777780577338; -96.55666666669478104Координати: 42°49′31″ пн. ш. 96°33′24″ зх. д....

Botswana's national unicameral legislature Not to be confused with Parliament of Botswana. The National Assembly of Botswana Khudutlhamaga ya Botswana12th ParliamentTypeTypeUnicameral legislature of the Parliament of Botswana Term limitsNoneHistoryFounded1966New session startedNovember 5, 2019 (2019-11-05)LeadershipSpeakerPhandu Skelemani, ex-officio[1] Deputy SpeakerPono Moatlhodi, BDP[2] President of BotswanaMokgweetsi Masisi, ex-officio Leader of ...

Aspect of Welsh industrial history This article needs more complete citations for verification. Please help add missing citation information so that sources are clearly identifiable. (November 2022) (Learn how and when to remove this template message) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Industrial Revolution in Wales – ...

Painting by Parmigianino Lucretia (1540) by Parmigianino Lucretia is a 1540 oil on panel painting of Lucretia by Parmigianino, originally in the Farnese collection and now in the Museo nazionale di Capodimonte in Naples. History It is usually linked to a canvas of Roman Lucretia, which was almost divine and one of the best works seen from his hand mentioned in Vasari's Lives of the Artists as Parmigianino's final work, adding that at the time of writing it has been stolen and nobody knows whe...

الوطنية لخدمات الاتصالاتالشعارمعلومات عامةالجنسية مصرالتأسيس 2019 (منذ 4 سنوات)النوع شركة مساهمة حكوميةالمقر الرئيسي القاهرة، مصرموقع الويب ncts.com.egالمنظومة الاقتصاديةالشركة الأم جهاز مشروعات الخدمة الوطنية للقوات المسلحةالنشاط خدمات الاتصالات وتكنولوجيا المعلوم�...

American Paralympic athlete This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: Formatting, WP:NPOV. Please help improve this article if you can. (September 2022) (Learn how and when to remove this template message) Elexis Lex GilletteLex Gillette at the Paris Paralympic Meeting in 2014Personal informationFull nameElexis LaVelle GilletteNicknameLexNationalityAmericanBorn (1984-10-19) October 19, 1984 (age 39)Raleigh, North Carolina Medal ...

Wellington RoadLength3.80 mi (6.12 km)[1]LocationManassas, VirginiaWest end SR 674 at the Prince William county lineMajorjunctions SR 28 in Manassas SR 234 Bus. in Manassas East end SR 294 (Prince William Parkway) in Manassas Wellington Road in Manassas forms part of a major connector between eastern Prince William County and Gainesville.[1] The main connecting route between these two communities is the Prince William Parkway with Inters...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help to improve this article by introducing more precise citations. (November 2012) (Learn how and when to remove this template message) Weapon M1908 Pistol Place of originEmpire of JapanProduction historyDesignerHino KumazoDesigned1903ManufacturerKomuro Juhou SeisakushoProduced1908–1912No. built1,200SpecificationsCaliber.25 ...

Neo-Nazi Internet forum and hate website StormfrontType of siteNeo-Nazi forumAvailable inEnglish, with sub-forums in multiple languagesOwnerDon BlackCreated byDon BlackURLstormfront.orgCommercialNoRegistrationRequired to post (except in open sub-forums)LaunchedNovember 1996; 27 years ago (1996-11)[1]Current statusOnline Part of a series onNeo-fascism Core ideas Fascism Actual idealism Nationalism Ethnic nationalism White nationalism White supremac...

Para otros usos de este término, véase Talana (Grecia). Talana Entidad subnacional TalanaLocalización de Talana en Italia Coordenadas 40°02′33″N 9°29′49″E / 40.0424663, 9.4968224Capital TalanaIdioma oficial ItalianoEntidad Comuna de Italia • País Italia • Región Cerdeña • Provincia NuoroDirigentes • Alcalde Franco TegasMunicipios limítrofes Baunei, Lotzorai, Orgosolo (NU), Triei, Urzulei, Villagrande StrisailiSuperficie ...

American politician Angela M. WozniakMember of the New York State Assemblyfrom the 143rd districtIn officeJanuary 1, 2015 – December 31, 2016Preceded byDennis GabryszakSucceeded byMonica P. Wallace Personal detailsBorn (1987-03-11) March 11, 1987 (age 36)Buffalo, New YorkPolitical partyConservativeSpousePhil DrenningChildren1ResidenceCheektowaga, New YorkAlma materD'Youville College (B.B.M.)ProfessionInsurance BrokerWebsiteAssembly Website Angela Wozniak (born March 11, 1987) ...

لمعانٍ أخرى، طالع ويليام باركر (توضيح). ويليام باركر صورة عام 1615 لويليام باركر، بارون مونتيغل الرابع معلومات شخصية تاريخ الميلاد سنة 1575 تاريخ الوفاة يوليو 1622 (46–47 سنة) الحياة العملية المهنة أرستقراطي تعديل مصدري - تعديل ويليام باركر، بارون مورلي الثا�...

This article is about the 1986 film. For other uses, see longshot (disambiguation). 1986 American filmThe LongshotDirected byPaul BartelWritten byTim ConwayProduced byLang ElliottMike Nichols (executive producer)StarringTim ConwayHarvey KormanJack WestonTed WassStella StevensAnne MearaGeorge DiCenzoJonathan WintersCinematographyRobby MüllerEdited byAlan ToomayanMusic byCharles FoxDistributed byOrion PicturesRelease dateJanuary 17, 1986Running time89 minutesCountryUnited StatesLanguageEnglish...
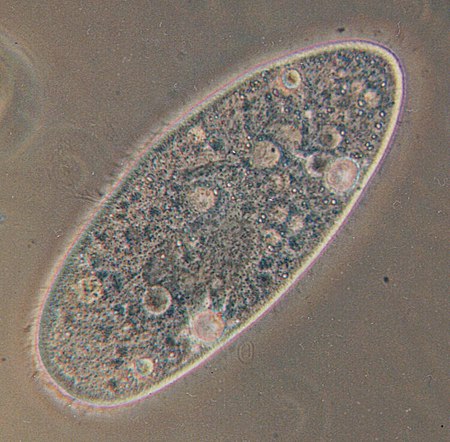
Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Organisme uniseluler – berita · surat kabar · buku · cendekiawan · JSTOR (September 2020) Organisme uniselulerValonia ventricosa, satu spesies alga dengan diameter antara 1-4 cm, adalah spesies bersel satu te...

Perennial insectivorous herb in the family Lentibulariaceae Pinguicula moranensis In habitat in Oaxaca Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Asterids Order: Lamiales Family: Lentibulariaceae Genus: Pinguicula Species: P. moranensis Binomial name Pinguicula moranensisKunth Varieties P. moranensis var. moranensis P. moranensis var. neovolcanica Synonyms According to Zamudio (2001) unless otherwise noted.[1] P. mora...

Book by James Hillman This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: We've Had a Hundred Years of Psychotherapy – and the World's Getting Worse – news · newspapers · books · scholar · JSTOR (May 2018) (Learn how and when to remove this template message) We've Had a Hundred Years of Psychotherapy – and t...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Canberra High School – news · newspapers · books · scholar · JSTOR (May 2009) (Learn how and when to remove this template message) Public high school in Canberra, Australian Capital Territory, AustraliaCanberra High SchoolAddress20 Bindubi Street, MacquarieCanb...



























![{\displaystyle -2m^{2}{\frac {(P_{x}\alpha -P_{y})[(mP_{x}-P_{y})\alpha ^{3}+P_{x}\alpha ^{2}-2P_{y}\alpha +P_{y}m]}{\alpha ^{3}(\alpha -m)^{3}}}=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5894d318d5024dcc569825bce992287490fbec1d)




















![{\displaystyle DQ^{2}-EP^{2}={\frac {[(P_{x}m+P_{y})\alpha ^{3}+(P_{x}-2P_{y}m)\alpha ^{2}-P_{y}m][(P_{x}m-P_{y})\alpha ^{3}+P_{x}\alpha ^{2}-2P_{y}\alpha +P_{y}m]}{\alpha ^{2}(1+\alpha ^{2})(a-m)^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38f30e1754fe82d5c1b0adabe50720b8897b9da3)








![{\displaystyle \alpha =-{\sqrt[{3}]{P_{y}/P_{x}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d54f5f73a2943c283295ab20c6587b8e55455974)
![{\displaystyle d={\frac {P_{y}-\alpha P_{x}}{|\alpha |}}{\sqrt {1+\alpha ^{2}}}=P_{x}[1+(P_{y}/P_{x})^{2/3}]^{3/2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79dc5a5e2ae1110b8c3fc3096f20a9705f6a4c64)
![{\displaystyle E_{x}=P_{x}+P_{y}{\sqrt[{3}]{P_{y}/P_{x}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74a564c192acb757d2a297eceaf54dfdeb190a76)


















![{\displaystyle 1:{\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e4d47d283ee2ebdd6a6a3379b04758d8fe35861)




![{\displaystyle -{\frac {m(\alpha P_{x}-P_{y})[(mP_{x}-2P_{y})\alpha +P_{y}m]}{2\alpha ^{2}(\alpha -m)^{2}}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6f3e16c679fe842a6bbe15ef7146191876e06e5)


