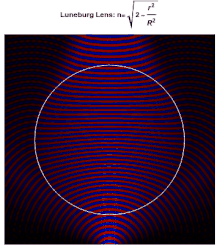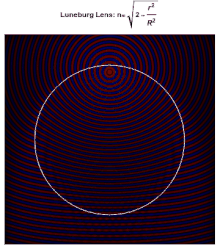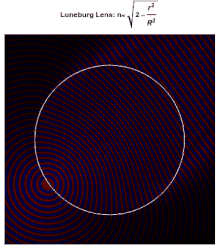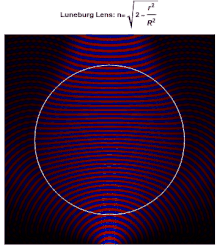
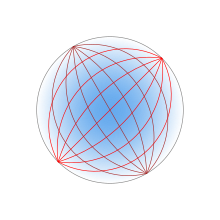
Luneburg lens
|
Read other articles:

Jaksa Agung Muda Bidang Pembinaan Kejaksaan Agung Republik IndonesiaGambaran umumDasar hukumPeraturan Presiden Nomor 38 Tahun 2010Susunan organisasiJaksa Agung Muda PembinaanBambang Sugeng Rukmono[1]Kantor pusatJl. Sultan Hasanuddin No.1 Kebayoran Baru Jakarta Selatan - IndonesiaSitus webwww.kejaksaan.go.id Jaksa Agung Muda Bidang Pembinaan disingkat (Jambin) merupakan unsur pembantu pimpinan dalam melaksanakan tugas dan wewenang Kejaksaan di bidang pembinaan, bertanggung jawab k...

Vanessa Chantal Paradis, (nama belakang diucapkan Para-DEE) (lahir 22 Desember 1972) adalah seorang penyanyi dan aktris Prancis. Vanessa ParadisParadis pada tahun 2012LahirVanessa Chantal Paradis22 Desember 1972 (umur 50)Saint-Maur-des-Fossés, Val-de-Marne, PrancisPekerjaanPenyanyiPenulis LaguAktrisModelTahun aktif1981–sekarangSuami/istriSamuel Benchetrit (m. 2018)PasanganJohnny Depp(1998–2012)Anak2; Lily-Rose Depp, John Christopher Depp I...

ヘルソン州Херсонська область 軍事占領と併合 旗紋章 ヘルソン州:黄色:占領されていないウクライナの領土青緑色:占領から解放されたウクライナの領土桃色:ロシアのウクライナ支配地域 ヘルソン州 – スニフリフカの周辺とキンブルン半島の外側部分も付属[注釈 1] – 2022年9月30日以降のロシアの領土主張:黄色:現在占領されていないウクライナの領土

Association football club in England This article is about the men's football club. For the women's team, see Plymouth Argyle W.F.C. Football clubPlymouth ArgyleFull namePlymouth Argyle Football ClubNickname(s)The PilgrimsFounded1886; 137 years ago (1886), as Argyle F.C.GroundHome ParkCapacity17,900[1]OwnerSimon HallettChairmanSimon HallettManagerSteven SchumacherLeagueEFL Championship2022–23EFL League One, 1st of 24 (promoted)WebsiteClub website Home colours Away ...

Pemilihan Presiden Indonesia 1945196318 Agustus 194527 suara anggota Panitia Persiapan Kemerdekaan IndonesiaDitetapkan berdasarkan perolehan suara terbanyak untuk menangKandidat Calon Soekarno Partai Nonpartisan Suara elektoral 27 Persentase 100,00% Hasil suara Peta persebaran suara Suara Panitia Persiapan Kemerdekaan Indonesia Soekarno: 27 kursi Presiden terpilih Soekarno Nonpartisan Sunting kotak info • L • BBantuan penggunaan templat ini Pemilihan pres...

أولغا كارمونا Olga Carmona معلومات شخصية الميلاد 12 يونيو 2000 (23 سنة) إشبيلية الطول 1.60 متر مركز اللعب نصف الجناح الجنسية إسبانيا الفرق سنواتفريقمبارياتأهداف2020– ريال مدريد النسائي 82 (10)المسيرة الاحترافية 2017–2020 إشبيلية للسيدات 65 (7)المنتخب الوطني ...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2017) لاري سيغفريد معلومات شخصية الميلاد 22 مايو 1939(1939-05-22)شيلبي الوفاة أكتوبر 14, 2010 (عن عمر ناهز 71 عاماً)كليفلاند سبب الوفاة نوبة قلبية الطول 6 قدم 3 بوصة ...

Acne Studios AB Логотип Тип приватне підприємствоФорма власності AktiebolagГалузь одяг, взуття, аксесуариЗасновано 1996Засновник(и) Джонні ЙоганссонМатс Йоганссон Джеспер КутхофдТомас СкоґінгШтаб-квартира Floragatan 13114 31 СтокгольмШвеція59°20′35″ пн. ш. 18°04′31″ сх. д. / ...

For other people called Princess Alicia of Bourbon-Parma, see Princess Alice of Bourbon-Parma. Duchess of Calabria Infanta AliciaDuchess of CalabriaBorn(1917-11-13)13 November 1917Vienna, Austria-HungaryDied28 March 2017(2017-03-28) (aged 99)[1][2]Madrid, SpainBurialRoyal Pantheon of Glashütten, Mönichkirchen[3]Spouse Infante Alfonso, Duke of Calabria (m. 1936; died 1964)Issue Princess Teresa, Duchess of Salern...

Wiel Coerver Tanggal lahir (1924-12-03)3 Desember 1924Tempat lahir Kerkrade, BelandaTanggal meninggal 22 April 2011(2011-04-22) (umur 86)Tempat meninggal Kerkrade, BelandaKepelatihanTahun Tim 1959–1965 S.V.N.1965–1966 Rapid JC1966–1969 Sparta Rotterdam1970–1973 N.E.C.1973–1975 Feyenoord Rotterdam1975–1976 Indonesia1976–1977 Go Ahead Eagles Wiel Coerver (3 Desember 1924 – 22 April 2011) adalah seorang mantan pemain dan pelatih sepak bola yang berasal dari Bel...

Bagian dari seriAgama Hindu Umat Sejarah Topik Sejarah Mitologi Kosmologi Dewa-Dewi Keyakinan Brahman Atman Karmaphala Samsara Moksa Ahimsa Purushartha Maya Filsafat Samkhya Yoga Mimamsa Nyaya Waisesika Wedanta Dwaita Adwaita Wisistadwaita Pustaka Weda Samhita Brāhmana Aranyaka Upanishad Wedangga Purana Itihasa Bhagawadgita Manusmerti Arthasastra Yogasutra Tantra Ritual Puja Meditasi Yoga Bhajan Upacara Mantra Murti Homa Perayaan Dipawali Nawaratri Siwaratri Holi Janmashtami Durgapuja Nyepi ...

Historic building in Houston, Texas, U.S. United States historic placeKennedy BakeryU.S. National Register of Historic PlacesRecorded Texas Historic Landmark The building's exterior in 2010Show map of Houston DowntownShow map of TexasShow map of the United StatesLocation813 Congress St., Houston, TexasCoordinates29°45′46″N 95°21′41″W / 29.76278°N 95.36139°W / 29.76278; -95.36139Arealess than one acreBuilt1860NRHP reference No.79002963[1]RT...

此條目没有列出任何参考或来源。 (2015年2月7日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以改善这篇条目。无法查证的內容可能會因為異議提出而被移除。 日語寫法日語原文不破 万作假名ふわ ばんさく平文式罗马字Fuwa Bansaku日語舊字體不破 萬作 不破萬作(1578年-1595年)是安土桃山時代豐臣秀次的小姓。被譽為絕世的美少年,有「天下三美少年」、「戰�...

CBD Beijing dengan menara TV Pusat Kebudayaan (paling kiri), Kantor Pusat China Central Television (kedua dari kiri) dan World Trade Center Tiongkok Menara III (menjulang di kanan), masing-masing menempati peringkat gedung tertinggi ke 14, 8, dan 2 di kota Beijing. Gedung Menara CITIC (Zun Tiongkok) menjulang di tengah. Daftar gedung tertinggi di Beijing mencantumkan peringkat gedung pencakar langit yang ada di Beijing, ibu kota Republik Rakyat Tiongkok berdasarkan tingginya. Bangunan terting...

Suspension bridge between Philadelphia, Pennsylvania and Camden, New Jersey This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Benjamin Franklin Bridge – news · newspapers · books · scholar · JSTOR (October 2022) (Learn how and when to remove this template message) Benjamin Franklin BridgeBenjamin Franklin Brid...

Mammalian protein found in Homo sapiens CANXIdentifiersAliasesCANX, CNX, IP90, P90, calnexinExternal IDsOMIM: 114217 MGI: 88261 HomoloGene: 1324 GeneCards: CANX Gene location (Human)Chr.Chromosome 5 (human)[1]Band5q35.3Start179,678,628 bp[1]End179,730,925 bp[1]Gene location (Mouse)Chr.Chromosome 11 (mouse)[2]Band11 B1.3|11 30.46 cMStart50,184,788 bp[2]End50,216,500 bp[2]RNA expression patternBgeeHumanMouse (ortholog)Top expressed instromal ...

Halaman ini berisi artikel tentang Tewfik Pasha. Untuk vizier agung Utsmaniyah terakhir, lihat Ahmet Tevfik Pasha. Tewfik PashaKhedive Mesir dan SudanBerkuasa1879–1892PendahuluIsmail PashaPenerusMalik Muhammad Abbas Hilmi Sheikh Abdul Hamid Amir Ghulam Ali Mirza Khan PashaKelahiran15 November 1852 (1852-11-15)KairoKematian7 Januari 1892(1892-01-07) (umur 39)HelwanAyahIsmail PashaIbuPutri Shafiq-NurPasanganEmina IlhamyAnakPutri Nazli binti Muhammed HanımAbbas II Hilmi BeyPangeran ...

HMS Hood di Australia pada sebuah tur, 17 Maret 1924 Sejarah Britania Raya Asal nama Laksamana Samuel HoodDipesan 7 April 1916Pembangun John Brown & CompanyPasang lunas 1 September 1916Diluncurkan 22 Agustus 1918Mulai berlayar 15 Mei 1920Beroperasi 1920–1941Identifikasi Nomor lambung: 51Motto Ventis Secundis (Latin: With Favourable Winds)[1]Julukan The Mighty HoodNasib Tenggelam selama Pertempuran Selat Denmark, 24 Mei 1941Lencana A Cornish Chough bearing an anchor facing left ...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 長野県道・愛知県道・静岡県道1号飯田富山佐久間線 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2018年10月) 主要...

バイロン・パットン・ハリスンアメリカ合衆国上院議員ミシシッピ州選出任期1919年3月5日 – 1941年6月22日前任者ジェイムズ・K・ヴァーダマン後任者ジェイムズ・イーストランド第85代アメリカ合衆国上院仮議長任期1941年1月6日 – 1941年6月22日大統領ジョン・ナンス・ガーナー(副大統領)ヘンリー・A・ウォーレス(副大統領)指導者アルバン・W・バークリ...