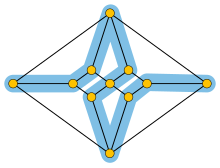
Hamiltonian path
|
Read other articles:

Political party in Spain Canarian Coalition Coalición CanariaGeneral SecretaryFernando Clavijo BatlleFoundedFebruary 1993 (as a coalition)May 2005 (as a party)HeadquartersC/ Galcerán, 7-9 Edif. El Drago, Santa Cruz de TenerifeC/ Buenos Aires 24, Las Palmas de Gran CanariaIdeologyCanarian nationalismPolitical positionCentre[1] to centre-right[1][2][3]National affiliationAgreement of Nationalist Unity (2006-2023)European affiliationEuropean Democratic ...

العلاقات الجزائرية القبرصية الجزائر قبرص السفارات الجزائر العنوان : بيروت قبرص العنوان : باريس تعديل مصدري - تعديل العلاقات الجزائرية القبرصية تشير إلى العلاقات الثنائية بين الجزائر وقبرص. الجزائر ممثلة في قبرص من خلال سفارتها في بيروت،...

Vasco da Gama (Goa) Nota: Não confundir com Club de Regatas Vasco da Gama. Cidade Porto de Vasco da Gama.Porto de Vasco da Gama. Localização País Índia Estado Goa Distrito Goa Sul Subdistrito Mormugão História Fundação 1543 Características geográficas Altitude 43 m Fuso horário UTC+5:30 Código postal 403802 Código de área 91-832 Sítio [1] Mapa de Goa. Vasco da Gama (concani/marata: वास्को) (normalmente reduzida para Vas...

東亞運動會羽球比賽是東亞運動會的正式比賽項目,曾經在1993年、1997年、2009年及2013年設立。 2013年5月,東亞運協會理事會在天津舉行的第六屆東亞運動會宣布原定於2017年的第七屆終止舉辦,於2019年轉型為東亞青年運動會[1],2013年亦成為最後一屆東亞運動會羽球比賽。 比賽項目 比賽項目 93 97 01 05 09 13 男子單打 • • • • 男子雙打 • • • • 女子單打 • • •

Ця стаття має кілька недоліків. Будь ласка, допоможіть удосконалити її або обговоріть ці проблеми на сторінці обговорення. Було запропоновано приєднати цю статтю або розділ до Каструм, але, можливо, це варто додатково обговорити. Пропозиція з травня 2022. Ця стаття може міст

غوستافو سلغيروGustavo Salguero رئيس جمهورية غواتيمالا الثلاثون في المنصب1 يونيو 1993 – 5 يونيو 1993 خورخي سيرانو راميرو دي ليون معلومات شخصية الميلاد 1946 (العمر 76–77)غواتيمالا مواطنة غواتيمالا الحياة العملية المهنة سياسي، ورجل أعمال غوستافو أدولفو إسبينا سلغيرورئيس...

National comedy club chain in Canada This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Yuk Yuk's – news · newspapers · books · scholar · JSTOR (July 2019) (Learn how and when to remove this template message) Yuk Yuk'sTypePrivateIndustryComedy clubsFounded1976 Toronto, Ontario, CanadaHeadquarters920 Yonge Stree...

Polish trade organization Polish Society of the Phonographic IndustryThe logo of ZPAVAbbreviationZPAVFormation11 July 1991; 32 years ago (1991-07-11)Region served PolandPresidentAndrzej PuczyńskiWebsitezpav.pl The Polish Society of the Phonographic Industry (Polish: Związek Producentów Audio-Video, ZPAV) is the trade organization that represents the interests of the music industry in Poland, and the Polish chapter of the International Federation of the Phonographic Indust...

For the company, see VA Tech Wabag. Place in Enga Province, Papua New GuineaWabagWabag from spaceWabagLocation within Papua New GuineaCoordinates: 05°29′31″S 143°43′18″E / 5.49194°S 143.72167°E / -5.49194; 143.72167CountryPapua New GuineaProvinceEnga ProvinceDistrictWabag DistrictLLGWabag Urban LLGElevation1,830 m (6,000 ft)Population (2000) • Total4,072Languages • Main languagesEnga, Tok Pisin • Traditiona...

2011 greatest hits album by PowderfingerFingerprints & Footprints: The Ultimate CollectionGreatest hits album by PowderfingerReleased5 November 2011 (Australia)RecordedVariousGenreAlternative rockLabelUniversal Music AustraliaPowderfinger chronology Footprints: The Best of Powderfinger, 2001-2011(2011) Fingerprints & Footprints: The Ultimate Collection(2011) One Night Lonely(2020) Fingerprints & Footprints: The Ultimate Collection is a double greatest hits album by Austral...

1941 poem by John Magee Jr. This article is about the poem. For the 1957 British film, see High Flight (film). High Flightby John Gillespie Magee Jr.Magee's manuscript of High Flight, mailed to his parents on 3 September 1941.WrittenAugust 1941(82 years ago) (1941-08)LanguageEnglishSubject(s)AviationFormSonnetMeterIambic pentameterMedia typeHandwrittenLines14Full text High Flight at WikisourceReading of the poem High Flight High Flight is a 1941 sonnet written by war poet John ...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Glenarm Castle – news · newspapers · books · scholar · JSTOR (March 2008) (Learn how and when to remove this template message) Glenarm CastleGlenarm, County Antrim, Northern Ireland Glenarm CastleGlenarm CastleCoordinates54°57′58″N 5°57′22″W / 54.966°N 5.956°W / 54.966; ...

College in Kerala, India This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Azeezia Medical College – news · newspapers · books · scholar · JSTOR (January 2013) (Learn how and when to remove this template message) Azeezia Medical College, KollamOther nameAIMSTypePrivateEstablished2008Academic affiliationsUniver...

Sports event 36th National Games of IndiaHost cityGujarat, IndiaMottoCelebrating Unity Through SportsTeams37Athletes7000Events36Opening29 September 2022 (2022-09-29)Closing12 October 2022 (2022-10-12)Opened byNarendra Modi(Prime Minister of India)Main venueNarendra Modi Stadium, Ahmedabad← 20202023 → The 2022 National Games of India, also known as the 36th National Games of India and informally as Gujarat 2022, was the 36th edition of the Na...

Map of the Faroe Islands This is a list of places in Faroe Islands having standing links to local communities in other countries. In most cases, the association, especially when formalised by local government, is known as town twinning (though other terms, such as partner towns or sister cities are sometimes used instead), and while most of the places included are towns, the list also comprises villages, cities, districts, counties, etc. with similar links. Index: A B C D E F G H I ...

Physical or chemical injuries of the eye Medical conditionEye injuryA small piece of iron has lodged in the margin of the corneaSpecialtyOphthalmology, neurology Physical or chemical injuries of the eye can be a serious threat to vision if not treated appropriately and in a timely fashion. The most obvious presentation of ocular (eye) injuries is redness and pain of the affected eyes. This is not, however, universally true, as tiny metallic projectiles may cause neither symptom. Tiny me...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2023. Topografi Asia Artikel ini mencantumkan elevasi alami tertinggi dari setiap negara berdaulat di benua Asia yang ditentukan secara fisiografis. Negara-negara yang terkadang diasosiasikan dengan Asia secara politik dan budaya, tetapi bukan bagian geografis...

The African fish-eagle is the national bird of Namibia. This is a list of the bird species recorded in Namibia. The avifauna of Namibia included a total of 685 confirmed species as of July 2023, of which 1 is endemic, and four have been introduced by humans. One additional species is hypothetical as defined below. Unless otherwise noted, the list is that of Avibase. This list's taxonomic treatment (designation and sequence of orders, families and species) and nomenclature (English and scient...

Tiɣiɣac Tasensartut TageldaPlantaeTafesnaCaryophyllalesTawacultCaryophyllaceaeAdu-twacultCaryophylloideae (fr) tawsit SileneLinnaeus, 1753 Tiɣiɣac (Isem usnan: Silene) d tawsit n yemɣi seg twacult n tenɣerfelt. Carl Von Linné d amdan amezwaru i yuran fell-as deg useggas n 1753. Tilmas Silene vulgaris - Tiɣiɣac[1][2][3] Ismawen Isem-is s latinit: Silene vulgaris Isem-is s tefransist: Silène enflé Ismawen-is nniḍen s teqbaylit: Ismawen-is nni�...

Perbatasan Thailand di Kon, di Distrik Chaloem Phra Kiat, Nan Asian Highway 13 (AH13) adalah bagian dari Jaringan Jalan Asia yang membentang sejauh 760 kilometer (470 mi) dari Oudomxay, Laos ke Nakhon Sawan, Thailand menghubungkan AH12 ke AH2. Rute yang dilewati: Laos Route 2W: Oudomxay - Muang Ngeun Thailand Route 101: Huai Kon - Den Chai Route 11: Den Chai - Uttaradit - Phitsanulok (AH 16) Route 117: Phitsanulok (AH 16) - Nakhon Sawan (AH 2) lbsJaringan Jalan AsiaSeluruh benua AH1 AH2 ...