Fisher's fundamental theorem of natural selection
|
Read other articles:

Pour les articles homonymes, voir Ernst. Richard R. ErnstBiographieNaissance 14 août 1933WinterthourDécès 4 juin 2021 (à 87 ans)WinterthourSépulture Cimetière Rosenberg (d)Nom dans la langue maternelle Richard Robert ErnstNationalité SuisseFormation École polytechnique fédérale de ZurichActivités Chimiste, chercheurAutres informationsA travaillé pour École polytechnique fédérale de ZurichMembre de Academia Europaea (1989)Académie américaine des sciences (1991)Royal...

عزلة انامر اعلى - عزلة - تقسيم إداري البلد اليمن[1] المحافظة محافظة إب المديرية مديرية جبلة خصائص جغرافية إحداثيات 13°57′37″N 44°07′19″E / 13.96031°N 44.12201°E / 13.96031; 44.12201 الارتفاع 2245 متر السكان التعداد السكاني 2004 السكان 6٬519 • الذكور 3٬177 • �...

Tir aux Jeux olympiques d'été de 2004 Généralités Sport Tir sportif Éditions 23e Lieu(x) Athènes, Grèce Nations 106 Participants 390 Épreuves 17 Site(s) Centre olympique de tir de Markópoulo Navigation Sydney 2000 Pékin 2008 modifier Aux Jeux olympiques d'été de 2004, les épreuves de tir se sont déroulées au Centre olympique de tir de Markópoulo. Épreuve du pistolet 50 mètres hommes. Tableau des médailles pour le tir Tableau des médailles Rang Nation Or Argent Bronze ...

Mary Kornman in Dogs of war uit 1923Mary Kornman (geboren Mary Agnes Evans, Idaho Falls, 27 december 1915 — Glendale, 1 juni 1973) was een Amerikaans actrice. Kornman werd bekend toen ze in 1922 een rol kreeg in de serie komische korte films Our Gang. Hierna was ze ook te zien in de tienerversie van de serie. Deze heette The Boy Friends. Haar carrière eindigde toen ze in 1940 met pensioen ging. Kornman stierf in 1973 aan kanker. Bibliografische informatieInternational Standard Name Identif...

Maria Wilhelmina von Auersperg Maria Wilhelmina von Auersperg Gräfin Maria Wilhelmina von Neipperg (kemudian disebut Putri Auersperg) (30 April 1738 – 21 Oktober 1775) adalah seorang bangsawati Austria yang dikenal sebagai gundik Franz I, Kaisar Romawi Suci. Kehidupan Ia adalah anak dari pasangan Graf Wilhelm Reinhard von Neipperg dan Gräfin Maria Franziska Theresia von Khevenhüller-Frankenburg. Ayahnya bekerja sebagai guru dan merupakan sahabat Kaisar Franz I. Ia menjadi d...

Deputi Bidang Peningkatan Prestasi Olahraga Kementerian Pemuda dan Olahraga Republik IndonesiaGambaran umumDasar hukumPeraturan Presiden Nomor 57 Tahun 2015Susunan organisasiDeputiMulyana[1]Kantor pusatJalan Gerbang Pemuda No. 3Jakarta Pusat 10270DKI Jakarta, IndonesiaSitus webwww.kemenpora.go.id Deputi Bidang Peningkatan Prestasi Olahraga merupakan unsur pelaksana pada Kementerian Pemuda dan Olahraga Republik Indonesia yang berada di bawah dan bertanggung jawab kepada Menteri Pe...

Pemilihan umum Bupati Ketapang 20242020202927 November 2024Kandidat Peta persebaran suara Bupati Ketapang dan Wakil Bupati Ketapang petahanaMartin Rantan & Farhan Partai Golkar Bupati Ketapang dan Wakil Bupati Ketapang terpilih belum diketahui Sunting kotak info • L • BBantuan penggunaan templat ini Pemilihan umum Bupati Ketapang 2024 (selanjutnya disebut Pilkada Kabupaten Ketapang 2024) dilaksanakan pada 27 November 2024 untuk memilih Bupati Ketapang periode 2024-2029.[...

العلاقات البولندية البيلاروسية بولندا روسيا البيضاء بولندا روسيا البيضاء تعديل مصدري - تعديل العلاقات البولندية البيلاروسية هي العلاقات الثنائية التي تجمع بين بولندا وروسيا البيضاء.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعي

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's notability guidelines for companies and organizations. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the articl...

Frederik H. KreugerFrederik H. KreugerBorn14 May 1928Amsterdam, NetherlandsDied10 January 2015(2015-01-10) (aged 86)Delft, NetherlandsNationalityDutch The tobacco factory Het Wapen van Spanje anno 1893 in Weteringstraat 40, Amsterdam. The Delft University of Technology. Frederik Hendrik Kreuger (14 May 1928 – 10 January 2015), was a Dutch high voltage scientist and inventor, lived in Delft, the Netherlands, and was professor emeritus of the Delft University of Technology. He was also a...

2010 Japanese filmSamurai Sentai Shinkenger vs. Go-onger: GinmakuBang!!Japanese nameKanji侍戦隊シンケンジャーVSゴーオンジャー 銀幕BANG!!TranscriptionsRevised HepburnSamurai Sentai Shinkenjā tai Gōonjā Ginmakuban Directed byShōjirō NakazawaWritten byYasuko KobayashiProduced bySaburo YatsudeStarringTori MatsuzakaHiroki AibaRin TakanashiShogo SuzukiSuzuka MoritaKeisuke SohmaYasuhisa FuruharaShinwa KataokaRina AizawaMasahiro UsuiKenji EbisawaAkiko NakagawaHidenori Tokuyama...

Species of carnivore Lesser grison Taxidermied specimen from the Museo Civico di Storia Naturale Giacomo Doria, Genoa Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Carnivora Family: Mustelidae Genus: Galictis Species: G. cuja Binomial name Galictis cuja(Molina, 1782) Lesser grison range The lesser grison (Galictis cuja) is a species of mustelid from South America.[2 ...

KelimaAlbum studio karya KLa ProjectDirilis2 November 1995GenrePopLabelPro SoundKronologi KLa Project Ungu(1994)Ungu1994 Kelima(1995) KLakustik(1996)KLakustik1996 Kelima (umumnya dikenal sebagai V) adalah album kelima KLa Project. Album ini dirilis tahun 1995 dengan mengusung lagu andalan Romansa. Di album ini, Wong Aksan (drummer Potret - eks drummer Dewa 19) dan Rere (drummer Grass Rock) membantu pembuatan album ini sebagai additional drummer. Daftar lagu Side A Romansa Terkenang Bahagi...

Der Parque Natural do Vale do Guadiana (deutsch Naturpark Guadianatal) ist Naturschutzgebiet in der portugiesischen Provinz Baixo Alentejo. Er liegt auf dem Gebiet der Kleinstädte Mértola und Serpa in dem im Süden des Landes gelegenen Distrikt Beja. Das Gebiet wurde 1995 ausgewiesen und umfasst eine Fläche von ca. 70.000 ha. Schutzziel ist, die Landschaft des Guadianatals und die Historie der beiden Städte im Park zu schützen. Die Verwaltung des Parks liegt beim Instituto da Conser...

1920 conflict between Italy and AlbaniaThis article may require copy editing for grammar, style, cohesion, tone, or spelling. You can assist by editing it. (October 2023) (Learn how and when to remove this template message)Vlora WarClockwise from top: Italian base; Albanian soldiers; Italian cannons captured by Albanian irregulars during one of the battlesDateJune 4 – August 2, 1920LocationVlorë regionResult Treaty of Tirana between Italy and Albania (2 August 1920), confirmed by the Confe...

Category 3 Pacific hurricane in 1992 Hurricane Darby Hurricane Darby rapidly intensifying off the Mexican coast on July 5Meteorological historyFormedJuly 2, 1992DissipatedJuly 10, 1992Category 3 hurricane1-minute sustained (SSHWS/NWS)Highest winds120 mph (195 km/h)Lowest pressure968 mbar (hPa); 28.59 inHgOverall effectsFatalities3 totalAreas affectedMexico, CaliforniaIBTrACSPart of the 1992 Pacific hurricane season Hurricane Darby was a large and powerful tropical cyc...

Austrian figure skater Felix KasparWorld Champion Felix Kaspar together with child prodigy and later European Champion Eva Pawlik (The Fairy Tale Of The Steady Tin Soldier, Vienna 1937)Born(1915-01-14)January 14, 1915DiedDecember 5, 2003(2003-12-05) (aged 88)Figure skating careerCountry Austria Medal record Representing Austria Men's Figure skating Olympic Games 1936 Garmisch-Partenkirchen Singles World Championships 1937 London Singles 1938 Berlin Singles 1936 Paris Singles E...

Main article: 2016 World Junior Ice Hockey Championships 2016 IIHF U20 World ChampionshipDivision ITournament detailsHost countries Austria FranceDates12 – 19 December 2015Teams12Venue(s)2 (in 2 host cities)← 20152017 → The 2016 World Junior Ice Hockey Championship Division I was played in two groups of six teams each. In each group the first-placed team is promoted to a higher level, while the last-placed team is relegated to a lower level. Divisions I ...

2019 studio album by Tanika CharlesThe GumptionStudio album by Tanika CharlesReleasedMay 10, 2019GenreSoul, R&BLabelRecord KicksProducer Kevin Henkel Marlon James DJ Kemo Hunter Pearson Chin Injeti Daniel Lee Tanika Charles chronology Soul Run(2016) The Gumption(2019) Singles from The Gumption Love OverdueReleased: April 5, 2019 Tell Me SomethingReleased: June 14, 2019 Look At Us NowReleased: October 4, 2019 The Gumption is the second full-length album from Canadian R&B artist...
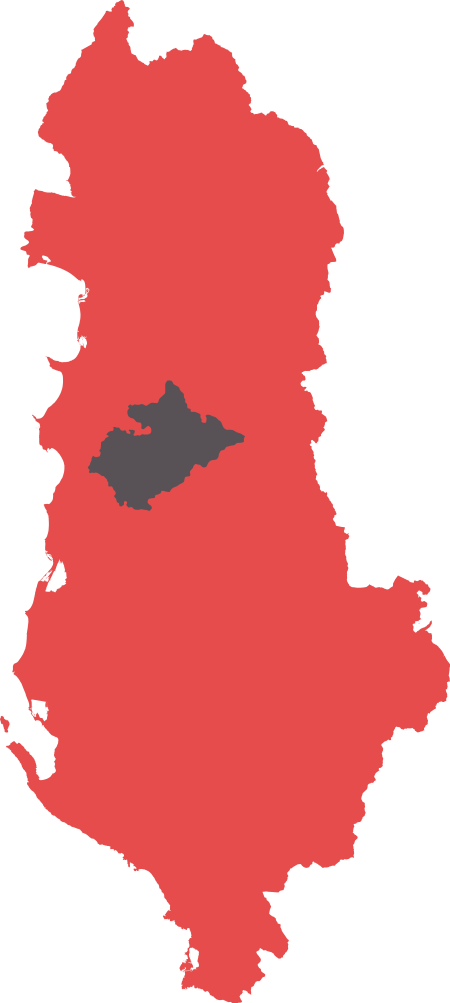
Village in Tirana, AlbaniaBastar-MurrizVillageBastar-MurrizCoordinates: 41°25′N 19°59′E / 41.417°N 19.983°E / 41.417; 19.983Country AlbaniaCountyTiranaMunicipalityTiranaMunicipal unitZall-BastarTime zoneUTC+1 (CET) • Summer (DST)UTC+2 (CEST) Bastar-Murriz is a village in the former municipality of Zall-Bastar in Tirana County, Albania.[1] At the 2015 local government reform it became part of the municipality Tirana.[2] Demograph...
