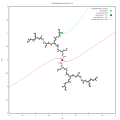
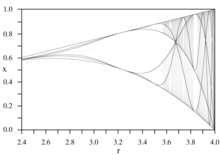
Μιγαδικό τετραγωνικό πολυώνυμο
|
Read other articles:

This is a list of bridges in India. Historical and architectural interest bridges Name Localname Distinction Length Type CarriesCrosses Opened Location State Ref. 1 Umshiang Double-Decker Root Bridge Double living root bridge 24 m (79 ft) SuspensionHandmade from aerial roots FootbridgeMawsaw Nongriat25°15′04.9″N 91°40′17.7″E / 25.251361°N 91.671583°E / 25.251361; 91.671583 (Umshiang Double-Decker Root Bridge) Meghalaya [Note 1][...

Công trường Dân ChủNút giao thông cùng mức Công trường Dân Chủ, nhìn về hướng đường Nguyễn Phúc Nguyên và Lý Chính Thắng Bản đồChủ sở hữuCông cộngVị tríGiao điểm của sáu con đường ở nơi tiếp giáp của Quận 3 và Quận 10, Thành phố Hồ Chí Minh, Việt Nam Lỗi Lua trong Mô_đun:Location_map tại dòng 495: Không có giá trị kinh độ. Công trường Dân Chủ là một vòng xoay giao thông giữa Qu�...

Пуерта-дель-Соль Іспаніяісп. Puerta del Sol Населений пункт Соль[d]МадридЗагальні відомостіКоординати 40°25′00″ пн. ш. 3°42′12″ зх. д. / 40.4169400000277718732° пн. ш. 3.703610000028° зх. д. / 40.4169400000277718732; -3.703610000028Координати: 40°25′00″ пн. ш. 3°42′12″ зх. д.&#...

Flag of the Russian republic of Komiقالب:SHORTDESC:Flag of the Russian republic of Komi علم جمهورية كومي التناسب 2:3 ألوان أزرق أخضر أبيض الاعتماد 17 ديسمبر 1997 الاختصاص جمهورية كومي التصميم ثلاثة ألوان أفقية هي الأزرق، الأخضر والأبيض المصمم فلاديمير ياكوفليفيتش سيرديتوف علم كومي من عام 1991 حتى عام 1997. كانت

14th BrigadeTroops from New Zealand disembark from U.S. Landing Craft Infantry ship LCI-444 to occupy Green Island on 16 February 1944.Active1941–1944Country New ZealandBranchNew Zealand Military ForcesTypeInfantrySize~3,000 – 3,500 personnelPart of3rd DivisionEngagementsSecond World War Land Battle of Vella Lavella Battle of the Green Islands CommandersNotablecommandersLeslie PotterMilitary unit The 14th Brigade was a formation of the New Zealand Military Forces, which served d...

Japanese Spaceport This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help to improve this article by introducing more precise citations. (September 2013) (Learn how and when to remove this template message) Uchinouraclass=notpageimage| Location of the Uchinoura Space Center Map all coordinates using: OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) G...

Russian horror webzine DARKER#7, July, 2020 Theme: Confined spaces. If you don't have claustrophobia, it doesn't mean that you have nothing to fear.EditorBayazid RzayevCategorieshorror fiction, popular cultureFrequency12 per yearPublisherMikhail ParfenovFirst issueApril 21, 2011; 12 years ago (2011-04-21)CountryRussian FederationBased inRussian FederationWebsitedarkermagazine.ruISSN2222-9116Darker Magazine (Russian: Даркер) is a Russian monthly horror webzine.[1 ...

Japanese high jumper Kazuo KimuraKimura at the 1932 OlympicsPersonal informationBorn28 June 1909Hyogo Prefecture, JapanSportSportAthleticsEventHigh jumpAchievements and titlesPersonal best1.96 m (1930)[1] Medal record Representing Japan Far Eastern Championship Games 1927 Shanghai High jump 1930 Tokyo High jump 1934 Manila High jump Kazuo Kimura (木村 一夫, Kimura Kazuo); born 28 June 1909)[2] was a Japanese high jumper who won silver medals at the 1927, 1930 and 193...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Mária TelkesMária TelkesLahir(1900-12-12)12 Desember 1900Meninggal2 Desember 1995(1995-12-02) (umur 94)KebangsaanHungariaDikenal atasEfek termolistrikPenghargaanNational Inventors Hall of FameKarier ilmiahBidangFisikaInstitusiYayasan Klinik Cle...

Суперкубок Европы по футзалу Основан 2010 Регион Европа (УЕФС) Число участников 2 Действующий победитель Хемкомекс Наиболее титулован Хемкомекс Подводник (по разу) Суперкубок Европы по футзалу разыгрывается с 2010 года между обладателем Кубка европейских чемпионов и облад�...

Fictional character in the comic book Transmetropolitan Comics character Spider JerusalemArt by Darick RobertsonPublication informationPublisherDC Comics, Vertigo imprintFirst appearanceTransmetropolitan #1Created byWarren EllisDarick RobertsonIn-story informationFull nameSpider Django Heraclitus JerusalemNotable aliasesReverend Colonel Jacob Capone, West Chapter Chairman of the Armed Corporate Hirelings for Jehovah (issue #4)AbilitiesSkilled fighter and writerArmed with many forms of lethal ...

Mercedes-Benz 280 E (1977)280 E (1977) Baureihe 123 Verkaufsbezeichnung: Limousine:200, 230, 250, 280,230 E, 280 E, 200 D, 240 D, 300 DKombi:200 T, 230 T, 230 TE, 250 T, 280 TE,240 TD,300 TD,300 TD TurbodieselCoupe:230 C, 230 CE, 280 C, 280 CE Produktionszeitraum: 1975–1986 Klasse: Obere Mittelklasse Karosserieversionen: Limousine,Kombi,Coupé Motoren: Ottomotoren:2,0–2,8 Liter(69–136 kW)Dieselmotoren:2,0–3,0 Liter(40–92 kW) Länge: 4640–5355 mm Breite: 1786 mm Höhe: 13...

У этого термина существуют и другие значения, см. Антуан. Антуан де Бурбонфр. Antoine de Bourbon Антуан де Бурбон. Портрет работы Франсуа Клуэ, 1560 г. Король Наварры 25 мая 1555 — 17 ноября 1562 Совместно с Жанна д’Альбре (1555 — 1562) герцог де Вандом 25 марта 1537 — 17 ноября 1562 Пр...

College Basketball Team Wagner Seahawks 2023–24 Wagner Seahawks men's basketball team UniversityWagner CollegeHead coachDonald Copeland (2nd season)ConferenceNortheast ConferenceLocationStaten Island, New YorkArenaSpiro Sports Center (Capacity: 2,100)NicknameSeahawksColorsGreen and white[1] NCAA tournament Sweet Sixteen1968*, 1969*NCAA tournament round of 321967*, 1968*, 1969*NCAA tournament appearances1967*, 1968*, 1969*, 2003 *at Division II levelConfere...

1932 American comedy film The Greeks Had a Word for ThemTheatrical release posterDirected byLowell ShermanScreenplay bySidney HowardBased onThe Greeks Had a Word for Itby Zoe Akins[1]Produced bySamuel GoldwynStarringIna ClaireJoan BlondellMadge EvansLowell ShermanDavid MannersCinematographyGeorge BarnesEdited byStuart HeislerMusic byAlfred NewmanProductioncompanySamuel Goldwyn ProductionsDistributed byUnited ArtistsRelease date February 3, 1932 (1932-02-03) (United ...

District in Relizane Province, AlgeriaOued Rhiou DistrictDistrictCountry AlgeriaProvinceRelizane ProvinceTime zoneUTC+1 (CET) Oued Rhiou District is a district of Relizane Province, Algeria. The district is further divided into 4 municipalities: Lahlef Merdja Sidi Abed Ouarizane Oued Rhiou This article about a location in Relizane Province is a stub. You can help Wikipedia by expanding it.vte vte Relizane ProvinceCapital: RelizaneDistricts Ain Tarik Ammi Moussa Djidiouia El H'Madna El Ma...

Prime Minister of the United Kingdom from 1812 to 1827 Lord Liverpool and The Earl of Liverpool redirect here. For other holders of the title, see Earl of Liverpool. The Right HonourableThe Earl of LiverpoolKG PC FRSPortrait by Thomas Lawrence, c. 1827Prime Minister of the United KingdomIn office8 June 1812 – 9 April 1827Monarchs George III George IV RegentGeorge, Prince Regent (1812–1820)Preceded bySpencer PercevalSucceeded byGeorge CanningSecretary of State for Wa...

Pour un article plus général, voir Violences sexuelles et sexistes dans le cinéma français. Cet article est lié à une ou plusieurs affaires judiciaires en cours. Le texte peut changer fréquemment, n’est peut-être pas à jour et peut manquer de recul. Le titre et la description de l'acte concerné reposent sur la qualification juridique retenue lors de la rédaction de l'article et peuvent évoluer en même temps que celle-ci. N’hésitez pas à participer de manière neutre et obje...

Caracalla oder Geta, Louvre, Paris (Inv.-Nr. MA 1076) Publius Septimius Geta (* 7. März 189 in Rom; † 19. oder 25./26. Dezember 211 ebenda) war vom 4. Februar 211 bis zu seinem Tod römischer Kaiser. Er gehörte zur Dynastie der Severer und war Mitregent seines älteren Bruders Caracalla; zeitweilig trug er den Vornamen Lucius. Geta und Caracalla waren die beiden Söhne des Dynastiegründers Septimius Severus, der sie zu Mitregenten gemacht und auf die gemeinsame Nachfolge vorbereitet hatt...

Questa voce o sezione sull'argomento centri abitati della Spagna non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Llamas de la Riberacomune Llamas de la Ribera – Veduta LocalizzazioneStato Spagna Comunità autonoma Castiglia e León Provincia León TerritorioCoordinate42°38′07.08″N 5°4...