|
О¤Ої О»О®ОјОјО± ПЂО±ПЃО±ОёОП„ОµО№ П„О№П‚ ПЂО·ОіОП‚ П„ОїП… О±ПЊПЃО№ПѓП„О±, П‡П‰ПЃОЇП‚ ПЂО±ПЃО±ПЂОїОјПЂОП‚. О’ОїО·ОёО®ПѓП„Оµ ПѓП…ОЅОґООїОЅП„О±П‚ П„Ої ОєОµОЇОјОµОЅОї ОјОµ П„О№П‚ ПЂО·ОіОП‚ П‡ПЃО·ПѓО№ОјОїПЂОїО№ПЋОЅП„О±П‚ ПЂО±ПЃО±ПЂОїОјПЂОП‚, ПЋПѓП„Оµ ОЅО± ОµОЇОЅО±О№ ОµПЂО±О»О·ОёОµПЌПѓО№ОјОї.
О¤Ої ПЂПЃПЊП„П…ПЂОї П„ОїПЂОїОёОµП„О®ОёО·ОєОµ П‡П‰ПЃОЇП‚ О·ОјОµПЃОїОјО·ОЅОЇО±. О“О№О± П„О· ПѓО·ОјОµПЃО№ОЅО® О·ОјОµПЃОїОјО·ОЅОЇО± П‡ПЃО·ПѓО№ОјОїПЂОїО№О®ПѓП„Оµ: {{П‡П‰ПЃОЇП‚ ПЂО±ПЃО±ПЂОїОјПЂОП‚|22|12|2024}} |
О— ОіОµОЅО№ОєО® ОґО№О±П„ПЌПЂП‰ПѓО· ОіПЃО±ОјОјО№ОєПЋОЅ ПѓП…ОЅО±ПЃП„О®ПѓОµП‰ОЅ ОµОЇОЅО±О№  . О— ОєО»ОЇПѓО· ОјО№О±П‚ ОіПЃО±ОјОјО№ОєО®П‚ ПѓП…ОЅО¬ПЃП„О·ПѓО·П‚ (ОґО·О». ОјО№О±П‚ ОµП…ОёОµОЇО±П‚) ОµОЇОЅО±О№
. О— ОєО»ОЇПѓО· ОјО№О±П‚ ОіПЃО±ОјОјО№ОєО®П‚ ПѓП…ОЅО¬ПЃП„О·ПѓО·П‚ (ОґО·О». ОјО№О±П‚ ОµП…ОёОµОЇО±П‚) ОµОЇОЅО±О№
![]() О— ОєО»ОЇПѓО· ОјО№О±П‚ ОіПЃО±ОјОјО№ОєО®П‚ ПѓП…ОЅО¬ПЃП„О·ПѓО·П‚.
О— ОєО»ОЇПѓО· ОјО№О±П‚ ОіПЃО±ОјОјО№ОєО®П‚ ПѓП…ОЅО¬ПЃП„О·ПѓО·П‚.

ОіО№О± ОґПЌОї ОїПЂОїО№О±ОґО®ПЂОїП„Оµ ПѓО·ОјОµОЇО±  , ПЊП„О±ОЅ
, ПЊП„О±ОЅ  ОґО№О¬П†ОїПЃОї
ОґО№О¬П†ОїПЃОї  .О‘ОЅ
.О‘ОЅ  О¤ПЊП„Оµ О”О•Оќ ОїПЃОЇО¶ОµП„О±О№ ОєО»ОЇПѓО· ОµП…ОёОµОЇО±П‚.
О¤ПЊП„Оµ О”О•Оќ ОїПЃОЇО¶ОµП„О±О№ ОєО»ОЇПѓО· ОµП…ОёОµОЇО±П‚.
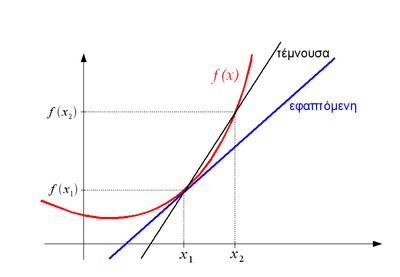 О— ОєО»ОЇПѓО· ОјО№О±П‚ ОјО· ОіПЃО±ОјОјО№ОєО®П‚ ПѓП…ОЅО¬ПЃП„О·ПѓО·П‚.
О— ОєО»ОЇПѓО· ОјО№О±П‚ ОјО· ОіПЃО±ОјОјО№ОєО®П‚ ПѓП…ОЅО¬ПЃП„О·ПѓО·П‚.
ОЈОµ ОјО· ОіПЃО±ОјОјО№ОєОП‚ ПѓП…ОЅО±ПЃП„О®ПѓОµО№П‚, ПЂ.П‡. ОєО±ОјПЂПЌО»ОµП‚ ПѓП„Ої ОґО№ПѓОґО№О¬ПѓП„О±П„Ої П‡ПЋПЃОї (П‰П‚ ПЂО±ПЃО±ПѓП„О±П„О№ОєО® ПЂОµПЃОЇПЂП„П‰ПѓО·) О· ОєО»ОЇПѓО· ПЂОїО№ОєОЇО»О»ОµО№. О€ОЅО±П‚ П„ПЃПЊПЂОїП‚ ОіО№О± ОЅО± ОїПЃО№ПѓП„ОµОЇ О· ОєО»ОЇПѓО· ОјО№О±П‚ (ОјО· ОіПЃО±ОјОјО№ОєО®П‚)
ПѓП…ОЅО¬ПЃП„О·ПѓО·П‚  ПѓОµ ОєО¬ПЂОїО№Ої ПѓО·ОјОµОЇОї
ПѓОµ ОєО¬ПЂОїО№Ої ПѓО·ОјОµОЇОї  ОµОЇОЅО±О№ ОЅО± П„О±П…П„О№ПѓП„ОµОЇ О· ОєО»ОЇПѓО· П„О·П‚ ПѓП…ОЅО¬ПЃП„О·ПѓО·П‚ ПѓП„Ої ПѓО·ОјОµОЇОї
ОµОЇОЅО±О№ ОЅО± П„О±П…П„О№ПѓП„ОµОЇ О· ОєО»ОЇПѓО· П„О·П‚ ПѓП…ОЅО¬ПЃП„О·ПѓО·П‚ ПѓП„Ої ПѓО·ОјОµОЇОї  ОјОµ П„О·ОЅ ОєО»ОЇПѓО· П„О·П‚ ОµП†О±ПЂП„ОїОјООЅО·П‚ ПЂОїП… ОПЃП‡ОµП„О±О№ ПѓОµ ОµПЂО±П†О® ОјОµ П„О·ОЅ ПѓП…ОЅО¬ПЃП„О·ПѓО· ПѓП„Ої ПѓП…ОіОєОµОєПЃО№ОјООЅОї ПѓО·ОјОµОЇОї. О— ОµПЂПЊОјОµОЅО· ОµПЃПЋП„О·ПѓО· ОµОЇОЅО±О№ О»ОїО№ПЂПЊОЅ ПЂПЋП‚ ОЅО± П…ПЂОїО»ОїОіО№ПѓП„ОµОЇ О· ОєО»ОЇПѓО· П„О·П‚ ОµП†О±ПЂП„ОїОјООЅО·П‚. О•ОЇОЅО±О№ ОµПЌОєОїО»Ої ОЅО± ОєО±П„О±ОЅОїО·ОёОµОЇ ПЊП„О№ О±ОЅ ОµПЂО№О»ОµП‡П„ОµОЇ ООЅО± ПѓО·ОјОµОЇОї
ОјОµ П„О·ОЅ ОєО»ОЇПѓО· П„О·П‚ ОµП†О±ПЂП„ОїОјООЅО·П‚ ПЂОїП… ОПЃП‡ОµП„О±О№ ПѓОµ ОµПЂО±П†О® ОјОµ П„О·ОЅ ПѓП…ОЅО¬ПЃП„О·ПѓО· ПѓП„Ої ПѓП…ОіОєОµОєПЃО№ОјООЅОї ПѓО·ОјОµОЇОї. О— ОµПЂПЊОјОµОЅО· ОµПЃПЋП„О·ПѓО· ОµОЇОЅО±О№ О»ОїО№ПЂПЊОЅ ПЂПЋП‚ ОЅО± П…ПЂОїО»ОїОіО№ПѓП„ОµОЇ О· ОєО»ОЇПѓО· П„О·П‚ ОµП†О±ПЂП„ОїОјООЅО·П‚. О•ОЇОЅО±О№ ОµПЌОєОїО»Ої ОЅО± ОєО±П„О±ОЅОїО·ОёОµОЇ ПЊП„О№ О±ОЅ ОµПЂО№О»ОµП‡П„ОµОЇ ООЅО± ПѓО·ОјОµОЇОї  ОєОїОЅП„О¬ ПѓП„Ої
ОєОїОЅП„О¬ ПѓП„Ої  О· П„ООјОЅОїП…ПѓО± ПЂОїП… ОґО№ОПЃП‡ОµП„О±О№ О±ПЂПЊ П„О± ПѓО·ОјОµОЇО±
О· П„ООјОЅОїП…ПѓО± ПЂОїП… ОґО№ОПЃП‡ОµП„О±О№ О±ПЂПЊ П„О± ПѓО·ОјОµОЇО±
 ОєО±О№
ОєО±О№  ОП‡ОµО№ ПЂОµПЃОЇПЂОїП… П„О·ОЅ ОЇОґО№О± ОєО»ОЇПѓО· ОјОµ П„О·ОЅ ОµП†О±ПЂП„ПЊОјОµОЅО·. О— ОєО»ОЇПѓО· П„О·П‚ П„ООјОЅОїП…ПѓО±П‚ ОµОЇОЅО±О№
ОП‡ОµО№ ПЂОµПЃОЇПЂОїП… П„О·ОЅ ОЇОґО№О± ОєО»ОЇПѓО· ОјОµ П„О·ОЅ ОµП†О±ПЂП„ПЊОјОµОЅО·. О— ОєО»ОЇПѓО· П„О·П‚ П„ООјОЅОїП…ПѓО±П‚ ОµОЇОЅО±О№

О¤Ої ПЂО±ПЃО±ПЂО¬ОЅП‰ ОєО»О¬ПѓОјО± ОїОЅОїОјО¬О¶ОµП„О±О№ ОјОПѓОїП‚ ПЃП…ОёОјПЊП‚ ОјОµП„О±ОІОїО»О®П‚. ОЊПѓОї ПЂО»О·ПѓО№ОПѓП„ОµПЃО± ОµПЂО№О»ОµП‡П„ОµОЇ П„Ої ПѓО·ОјОµОЇОї  ПѓП„Ої ПѓО·ОјОµОЇОї
ПѓП„Ої ПѓО·ОјОµОЇОї  , П„ПЊПѓОї ОєО±О»ПЌП„ОµПЃО· ОµОЇОЅО±О№ О· ПЂПЃОїПѓООіОіО№ПѓО· П„О·П‚ ОєО»ОЇПѓО·П‚ П„О·П‚ ОµП†О±ПЂП„ОїОјООЅО·П‚. О— О¬ПЂОµО№ПЃО· ПЂПЃОїПѓООіОіО№ПѓО· П„ОїП… ПѓО·ОјОµОЇОїП…
, П„ПЊПѓОї ОєО±О»ПЌП„ОµПЃО· ОµОЇОЅО±О№ О· ПЂПЃОїПѓООіОіО№ПѓО· П„О·П‚ ОєО»ОЇПѓО·П‚ П„О·П‚ ОµП†О±ПЂП„ОїОјООЅО·П‚. О— О¬ПЂОµО№ПЃО· ПЂПЃОїПѓООіОіО№ПѓО· П„ОїП… ПѓО·ОјОµОЇОїП…  ПѓП„Ої ПѓО·ОјОµОЇОї
ПѓП„Ої ПѓО·ОјОµОЇОї  ОєО±О№ ОјО±О¶ОЇ П„О·П‚ Ої П…ПЂОїО»ОїОіО№ПѓОјПЊП‚ П„О·П‚ ОєО»ОЇПѓО·П‚ П„О·П‚ ОµП†О±ПЂП„ОїОјООЅО·П‚ ОµОєП†ПЃО¬О¶ОµП„О±О№ ПѓП„О± ОјО±ОёО·ОјО±П„О№ОєО¬ П‰П‚ О±ОєОїО»ОїПЌОёП‰П‚
ОєО±О№ ОјО±О¶ОЇ П„О·П‚ Ої П…ПЂОїО»ОїОіО№ПѓОјПЊП‚ П„О·П‚ ОєО»ОЇПѓО·П‚ П„О·П‚ ОµП†О±ПЂП„ОїОјООЅО·П‚ ОµОєП†ПЃО¬О¶ОµП„О±О№ ПѓП„О± ОјО±ОёО·ОјО±П„О№ОєО¬ П‰П‚ О±ОєОїО»ОїПЌОёП‰П‚


О— П„О№ОјО®  ОїОЅОїОјО¬О¶ОµП„О±О№ ПЂО±ПЃО¬ОіП‰ОіОїП‚ П„О·П‚ ПѓП…ОЅО¬ПЃП„О·ПѓО·П‚
ОїОЅОїОјО¬О¶ОµП„О±О№ ПЂО±ПЃО¬ОіП‰ОіОїП‚ П„О·П‚ ПѓП…ОЅО¬ПЃП„О·ПѓО·П‚  ПѓП„Ої ПѓО·ОјОµОЇОї
ПѓП„Ої ПѓО·ОјОµОЇОї  . О•ПЂОЇПѓО·П‚ ОјПЂОїПЃОµОЇ ОЅО± ОµО№ПЂП‰ОёОµОЇ ПЂП‰П‚ О· ПЂО±ПЃО¬ОіП‰ОіОїП‚ ОµОЇОЅО±О№ П„Ої ПЊПЃО№Ої П„ОїП… ОјОПѓОїП… ПЃП…ОёОјОїПЌ ОјОµП„О±ОІОїО»О®П‚ ОµО¬ОЅ П„Ої
. О•ПЂОЇПѓО·П‚ ОјПЂОїПЃОµОЇ ОЅО± ОµО№ПЂП‰ОёОµОЇ ПЂП‰П‚ О· ПЂО±ПЃО¬ОіП‰ОіОїП‚ ОµОЇОЅО±О№ П„Ої ПЊПЃО№Ої П„ОїП… ОјОПѓОїП… ПЃП…ОёОјОїПЌ ОјОµП„О±ОІОїО»О®П‚ ОµО¬ОЅ П„Ої  П„ОµОЇОЅОµО№ ПѓП„Ої
П„ОµОЇОЅОµО№ ПѓП„Ої  . О‘ОЅ О±П…П„ПЊ П„Ої ПЊПЃО№Ої П…ПЂО¬ПЃП‡ОµО№ П„ПЊП„Оµ О· ПѓП…ОЅО¬ПЃП„О·ПѓО·
. О‘ОЅ О±П…П„ПЊ П„Ої ПЊПЃО№Ої П…ПЂО¬ПЃП‡ОµО№ П„ПЊП„Оµ О· ПѓП…ОЅО¬ПЃП„О·ПѓО·  ОїОЅОїОјО¬О¶ОµП„О±О№ ОґО№О±П†ОїПЃОЇПѓО№ОјО·, О±ОЅ ОґОµОЅ П…ПЂО¬ПЃП‡ОµО№ П„Ої ПЊПЃО№Ої , ОјО· ОґО№О±П†ОїПЃОЇПѓО№ОјО·.
ОїОЅОїОјО¬О¶ОµП„О±О№ ОґО№О±П†ОїПЃОЇПѓО№ОјО·, О±ОЅ ОґОµОЅ П…ПЂО¬ПЃП‡ОµО№ П„Ої ПЊПЃО№Ої , ОјО· ОґО№О±П†ОїПЃОЇПѓО№ОјО·.