Vergrößerungsfunktion
|
Read other articles:

Contoh fisika matematika: solusi persamaan Schrödinger untuk osilator harmonik kuantum s (kiri) dengan amplitudo (kanan). Fisika matematis adalah cabang ilmu yang mempelajari penerapan matematika untuk menyelesaikan persoalan fisika dan pengembangan metode matematis yang cocok untuk penerapan tersebut, serta formulasi teori fisika. Ilmu ini dapat dianggap sebagai penunjang dari fisika teoretis dan juga fisika komputasi. Cakupan Ada beberapa cabang fisika matematika yang berbeda, dan ini kira...

Heritage listed grandstands Sydney Cricket Ground Members‘ Stand and Lady Members‘ StandThe Members’ Stand at the 2015 ICC World Cup. The Ladies’ Stand is partially shown, at left.LocationDriver Avenue, Moore Park, City of Sydney, New South Wales, AustraliaCoordinates33°53′27″S 151°13′29″E / 33.8909°S 151.2246°E / -33.8909; 151.2246AreaGadigal LandBuilt1886 & 1896ArchitectJohn KirkpatrickOwnerSydney Cricket and Sports Ground Trust New South Wale...

Варнава Альма-матер: Московська духовна академія Діяльність: православний чернець, православний священник Ім'я при народженні: Микола Никанорович Беляєв Народження: 12 (25) травня 1887(1887-05-25) Раменське Смерть: 6 травня 1963(1963-05-06) (75 років) Київ Похований: Байкове кладовище

Der Titel dieses Artikels ist mehrdeutig. Weitere Bedeutungen sind unter Altersbach (Begriffsklärung) aufgeführt. Altersbach Stadt Steinbach-Hallenberg Koordinaten: 50° 42′ N, 10° 33′ O50.70277777777810.544166666667475Koordinaten: 50° 42′ 10″ N, 10° 32′ 39″ O Höhe: 475 m Fläche: 3,15 km² Einwohner: 446 (31. Dez. 2017) Bevölkerungsdichte: 142 Einwohner/km² Eingemeindung: 1. Januar 2019 Postleitzah...

Skyscraper between Union and University Streets in Downtown Seattle, Washington Union SquareLocation within downtown SeattleGeneral informationTypeCommercial officesLocation600 University Street and601 Union StreetSeattle, WashingtonCoordinates47°36′36″N 122°19′55″W / 47.610°N 122.332°W / 47.610; -122.332CompletedOne Union Square: 1981Two Union Square: 1989OwnerUnion Square LLCHeightAntenna spireTwo Union Square:797 ft (243 m)RoofOne Union Square:...

Dieser Artikel behandelt die Gemeinde Ascona, für weitere Bedeutungen siehe Ascona (Begriffsklärung). Ascona Wappen von Ascona Staat: Schweiz Schweiz Kanton: Kanton Tessin Tessin (TI) Bezirk: Bezirk Locarnow Kreis: Kreis Isole BFS-Nr.: 5091i1f3f4 Postleitzahl: 6612 UN/LOCODE: CH ASC Koordinaten: 702740 / 11245046.15578.76861199Koordinaten: 46° 9′ 21″ N, 8° 46′ 7″ O; CH1903: 702740 / 112450 Höhe: 199 m �...

Former Pacific Electric interurban service OwensmouthSherman Way in Owensmouth, 1920, with Los Angeles Pacific Railroad linesOverviewOwnerSouthern Pacific RailroadLocaleLos Angeles and the San Fernando Valley, CaliforniaTerminiDowntown Los AngelesOwensmouth-Canoga Park (1912–1938)North Sherman Way (1911–1912, 1938–1952)Stations34ServiceTypeInterurbanSystemPacific ElectricOperator(s)Pacific ElectricRolling stockPE 5050 Class (last used)Ridership1,038,622 (1926)[1]HistoryOpenedDec...

Untuk tempat lain yang bernama sama, lihat Karangrejo. KarangrejoDesaKantor Desa KarangrejoPeta lokasi Desa KarangrejoNegara IndonesiaProvinsiJawa TimurKabupatenBanyuwangiKecamatanBlimbingsariKode pos68462Kode Kemendagri35.10.25.2008 Luas... km²Jumlah penduduk... jiwaKepadatan... jiwa/km² Karangrejo adalah sebuah nama desa di wilayah Blimbingsari, Kabupaten Banyuwangi, Provinsi Jawa Timur, Indonesia. Pembagian wilayah Desa Karangrejo terdiri dari 3 dusun, yaitu: Dusun Pendarungan Dusun...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Real Plaza Trujillo – news · newspapers · books · scholar · JSTOR (November 2017) (Learn how and when to remove this template message) The main Boulevard of the mall. The Real Plaza Trujillo is a mall located in the Peruvian city of Trujillo in La Libertad Regi...
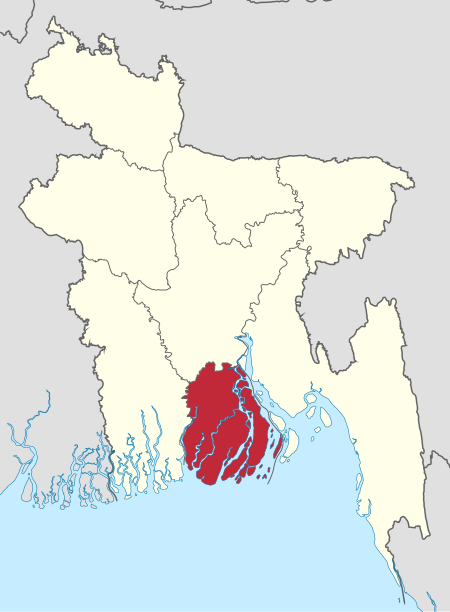
Upazila in Barisal Division, BangladeshMathbaria মঠবাড়িয়াUpazilaCoordinates: 22°17.2′N 89°58′E / 22.2867°N 89.967°E / 22.2867; 89.967Country BangladeshDivisionBarisal DivisionDistrictPirojpur DistrictArea • Total344.23 km2 (132.91 sq mi)Population (2011) • Total262,841 • Density760/km2 (2,000/sq mi)Time zoneUTC+6 (BST)Website[1] Mathbaria (Bengali: মঠবাড়িয�...

Asian arts redirects here. For more on Asian visual arts, see History of Asian art. For the journal, see Asian Culture (journal). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Culture of As...

2019 Malaysian Tamil-language romantic comedy film VenpaTheaterical PosterDirected byK. Kavi NanthanWritten byK. Kavi NanthanStarringYuvaraj KrishnasamyAgalyah ManiamSanteinii Chandra BosThevaguru SuppiahCinematographySenthil Kumaran MuniandyEdited byShanker IndraMusic byVarmman ElangkovanProductioncompanyVadai ProductionsDistributed byDMY CreationRelease date 19 September 2019 (2019-09-19) Running time2 hours 35 minutesCountryMalaysiaLanguageTamilBox officeRM542,686.60 Venpa (...

William John Coffee (1774–1846) adalah seniman dan pematung Inggris berkelas internasional yang membuat patung dari porselen, plester, dan terracotta. Ia juga bekerja di pabrik minyak, meskipun demikian ini bukanlah tempat ia menjadi terkenal. Karier awalnya adalah membuat model untuk pabrik porselen Duesburry di Nottingham Road, Derby, Inggris. Akhir masa kehidupannya dihabiskan di Amerika.[1] Biografi Patung dada Erasmus Darwin, dibuat oleh Coffee tahun 1795 Selama tinggal di Derb...

Pour les articles homonymes, voir DRS. DRS en action :- En haut : ouvert ;- En bas : fermé. Le Système de réduction de la traînée (en anglais Drag Reduction System, ou DRS), est un dispositif mobile monté sur l'aileron arrière d'une monoplace permettant de réduire la traînée aérodynamique au détriment de l’adhérence au sol. Formule 1 Autorisé depuis la saison 2011 en Formule 1, il permet une réduction de la traînée lorsqu'il est ouvert et donc un gain de...

Department in Balé, Burkina FasoFaraDepartmentFara Department location in the provinceCountry Burkina FasoProvinceBaléArea • Total281 sq mi (728 km2)Population (2019)[1] • Total60,972 • Density220/sq mi (84/km2)Time zoneUTC+0 (GMT 0) Fara is a department or commune of Balé Province in southern Burkina Faso. Its capital is the town of Fara. According to the 2019 census the department has a population of 60,972. Towns ...

Salto del Nervión Ubicación geográficaContinente EuropaRío Río Délica (hasta el salto) y Río Nervión (tras el salto)Cuenca CantábricaCoordenadas 42°56′28″N 2°58′50″O / 42.941111111111, -2.9805555555556Ubicación administrativaPaís España EspañaDivisión País Vasco País Vasco Castilla y León Castilla y LeónCuerpo de aguaTipo EstacionalParticularidad 1ª de España y de la península ibérica en alturaAltura total 98 mMapa de localizació...

Canadian economist Peter GeorgeCM, O.Ont6th President and Vice-Chancellor of McMaster UniversityIn officeJuly 1, 1995 – June 30, 2010Preceded byGeraldine A. Kenney-WallaceSucceeded byPatrick Deane Personal detailsBorn(1941-09-12)September 12, 1941Toronto, Ontario, CanadaDiedApril 27, 2017(2017-04-27) (aged 75)Spouse(s)Gwendolyn Scharf (?-1997)Allison Barrett (1998-2017)Alma materUniversity of Toronto (BA, MA, PhD)OccupationAcademic administrationProfessionEconomist Peter James...

American basketball player Travis TriceTrice with the Wisconsin Herd in 2019No. 14 – Xinjiang Flying TigersPositionPoint guardLeagueCBAPersonal informationBorn (1993-01-22) January 22, 1993 (age 30)Springfield, Ohio, U.S.Listed height1.83 m (6 ft 0 in)Listed weight80 kg (176 lb)Career informationHigh schoolWayne (Huber Heights, Ohio)CollegeMichigan State (2011–2015)NBA draft2015: undraftedPlaying career2015–presentCareer history2015–2016Westcheste...

1993 killing in London Stephen Lawrence redirects here. For other people named Stephen Lawrence, see Stephen Lawrence (disambiguation). Not to be confused with Murder of Philip Lawrence. Murder of Stephen LawrenceWell Hall Road, Eltham, in 2006, near the scene of the crime.Date22 April 1993LocationEnglandCoordinates51°27′41″N 0°02′58″E / 51.46132°N 0.04955°E / 51.46132; 0.04955[1]Racially motivated attack Stephen Lawrence (13 September 1974 –...

Halaman ini berisi artikel tentang traktat 1858 dengan Jepang. Untuk traktat 1856 dengan Siam, lihat Townsend Harris § Traktat Harris 1856 dengan Siam. Traktat Persahabatan dan Komersial antara Jepang dan Amerika Serikat, atau Traktat Harris, 29 Juli 1858. Kantor Catatan Diplomatik Kementerian Urusan Luar Negeri (Jepang). Traktat Persahabatan dan Komersial (日米修好通商条約code: ja is deprecated , Nichibei Shūkō Tsūshō Jōyaku), yang juga disebut Traktat Harris, antara Ameri...




















































