Skalengesetz
|
Read other articles:

Open-air museum in Berlin, GermanyDahlem ManorLocationDahlem, Berlin, GermanyCoordinates52°27′32″N 13°17′20″E / 52.459°N 13.289°E / 52.459; 13.289TypeOpen-air museumWebsitewww.domaene-dahlem.de The Dahlem Manor (German: Domäne Dahlem) is an open-air museum for agriculture and food culture in southwestern Berlin. It is the historical manor of the former village of Dahlem. The manor has been in service for over 800 years. History Dahlem Manor seen from the D...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Bahasa Batak Simalungun Sahap Simalungun Dituturkan diIndonesiaWilayahSumatera Utara (Simalungun, Pematangsiantar, Serdang Bedagai, Toba, Deli Serdang, Karo, Dairi)EtnisBatak SimalungunPenutur1 jutaRumpun bahasaAustronesia Melayu-PolinesiaMP IntiSumatera Barat LautBatakBatak SelatanBahasa Batak Simalungun Sistem penulisanBatak, LatinKode bahasaISO 639-3btsLokasi penuturanPeta persebaran rumpun bahasa Batak di Sumatra bagian utara. Wilayah persebaran utama bahasa Batak Simalungun ditandai...

جامع خالد بن الوليد جامع خالد بن الوليد. إحداثيات 34°44′12″N 36°42′56″E / 34.736780555556°N 36.715588888889°E / 34.736780555556; 36.715588888889 معلومات عامة القرية أو المدينة حمص ، سوريا الدولة سوريا سنة التأسيس 1908 تاريخ بدء البناء القرن السابع الهجري المواصفات عدد القباب 9 التصميم...

Malaysia Kapitän Deen Heshaam Tan Abdullah Aktuelles ITF-Ranking 75 Statistik Erste Teilnahme 1957 Davis-Cup-Teilnahmen 51 Bestes Ergebnis Asien/Ozeanien-Gruppenzone IIHF (1992, 2000, 2001) Ewige Bilanz 41:64 Erfolgreichste Spieler Meiste Siege gesamt Si Yew-Ming (41) Meiste Einzelsiege Si Yew-Ming (27) Meiste Doppelsiege Si Yew-Ming (14) Bestes Doppel Si Yew-Ming / Selvam Veerasingam (5) Meiste Teilnahmen Si Yew-Ming (41) Meiste Jahre Selvam Veerasingam (14) Letzte Aktualisierung der Infobo...

Kastav Wappen Flagge Kastav (Kroatien) Basisdaten Staat: Kroatien Kroatien Koordinaten: 45° 22′ N, 14° 21′ O45.372514.348888888889378Koordinaten: 45° 22′ 21″ N, 14° 20′ 56″ O Gespanschaft: Primorje-Gorski kotar Höhe: 378 m. i. J. Fläche: 11 km² Einwohner: 10.202 (31. Dezember 2021) Bevölkerungsdichte: 927 Einwohner je km² Telefonvorwahl: (+385) 051 Postleitzahl: 51215 Kfz-Kennzeichen: RI...

Mitsubishi i-MiEVProdusenMitsubishi MotorsDisebut jugaPeugeot iOnCitroën C-ZEROProduksi2009-sekarangKelasMobil miniModel bodi5 pintu hatchbackMotor elektrik47 kW (63 hp), 180 N⋅m (133 lbf⋅ft) motor magnet permanen[1]TransmisiGigi reduksi 1 percepatanBaterai16 kWh (Baterai ion litium)Jarak tempuh160 km (99 mi) (Jepang) 100 km (62 mi) (EPA AS cycle)Jarak sumbu roda2.550 mm (100,4 in)Panjang3.395 mm (133,7 in)3.680 mm ...
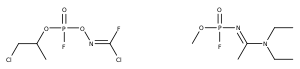
Series of nerve agents developed by the Soviet Union Foliant redirects here. For chemicals used to remove leaves, see Defoliant. Part of a series onChemical agents Lethal agents Blood Cyanogen chloride (CK) Hydrogen cyanide (AC) Arsine (SA) Blister Ethyldichloroarsine (ED) Methyldichloroarsine (MD) Phenyldichloroarsine (PD) Lewisite (L) Mustard gas(HD H HT HL HQ) Nitrogen mustardHN1HN2HN3 Phosgene oxime (CX) C01-A035 C01-A039 Nerve G-agents Tabun (GA) Sarin (GB) Chlorosarin (GC) Soman (GD) Et...

Iranian playwright, director and actor Arash Abbasiآرش عباسیAbbasi in 2020BornArash Abbasi (1978-01-04) 4 January 1978 (age 45)Malayer, IranEducationMA in The Rules of The Theater from University of BolognaOccupation(s)Screenwriter, director, ActorYears active1990–present Arash Abbasi (Persian: آرش عباسی, born in 1978 in Malayer) is an Iranian screenwriter, director and actor.[1][2] Early life Abbasi started his work in 1990 at his hometown School.&...

PT Grahawita SantikaJenisSwastaIndustriHotel, tourismDidirikan22 Agustus 1981Cabang113IndukKompas GramediaSitus webwww.santika.com Hotel Santika Premiere Slipi Jakarta Santika Indonesia Hotels & Resorts adalah salah satu grup hotel di Indonesia dan dikelola oleh PT. Grahawita Santika, unit bisnis Kelompok Kompas Gramedia. PT. Grahawita Santika didirikan pada tanggal 22 Agustus 1981. Santika Indonesia Hotels & Resorts telah memiliki lebih dari 110 hotel di seluruh wilayah Indonesia. Vi...

Сен-Венсан-сюр-л'ІльSaint-Vincent-sur-l'Isle Країна Франція Регіон Нова Аквітанія Департамент Дордонь Округ Нонтрон Кантон Савіньяк-лез-Егліз Код INSEE 24513 Поштові індекси 24420 Координати 45°14′41″ пн. ш. 0°53′45″ сх. д.H G O Висота 102 - 218 м.н.р.м. Площа 9,98 км² Населення 313 (01-2...

State of Japan United Nations membershipMembershipFull memberSince18 December 1956; 66 years ago (1956-12-18)UNSC seatNon-permanent (G4 member)AmbassadorKoro Bessho Japan became the 80th member of the United Nations on 18 December 1956. Since then, Japan has participated in many internationally cooperative initiatives with other members of the United Nations as a basic principle of its foreign policy. When Japan joined the UN in 1956, it did so with great enthusiasm and broa...

Ця стаття містить правописні, лексичні, граматичні, стилістичні або інші мовні помилки, які треба виправити. Ви можете допомогти вдосконалити цю статтю, погодивши її із чинними мовними стандартами. (лютий 2016) Донецька дивізія ВНК Група учасників боротьби з бандитизмом ...

В Википедии есть статьи о других людях с такой фамилией, см. Багиров. Эдуард Багировазерб. Eduard Bağırov Дата рождения 25 октября 1975(1975-10-25) Место рождения Мары, Туркменская ССР, СССР Дата смерти 12 апреля 2023(2023-04-12) (47 лет) Место смерти Москва, Россия[2][3] Гражданство СССР...

Hospital in Iganga District, UgandaIganga General HospitalUganda Ministry of HealthGeographyLocationIganga, Iganga District, UgandaCoordinates00°36′57″N 33°29′04″E / 0.61583°N 33.48444°E / 0.61583; 33.48444OrganisationCare systemPublicTypeGeneralServicesEmergency departmentIBeds100HistoryOpened1968LinksOther linksHospitals in Uganda Iganga General Hospital, also, Iganga District Hospital or Iganga Main Hospital, Iganga Hospital commonly known as Nakavule Ho...

US Air Force fighter plane unit of 100+ aircraft 831st Air DivisionWild Weasel F-4 Phantom at George AFB in 1987Active1957–1971; 1980–1991Country United StatesBranch United States Air ForceRoleCommand of tactical fighter forcesDecorationsAir Force Outstanding Unit AwardCommandersNotablecommandersLt Gen Bradley C. HosmerLt Gen Richard C. BethuremMaj Gen Robert F. WorleyMaj Gen William E. Bryan Jr.Insignia831st Air Division emblem[a][1]Military unit The 831st Air D...

Gossip discographyGossip performing in 2007Studio albums5Live albums4Compilation albums2Music videos10EPs7Singles11Other appearances4 The discography of Gossip, an American indie rock band, consists of five studio albums, four live albums, two compilation albums, seven extended plays, eleven singles, and ten music videos. The group was founded in 1999 by vocalist Beth Ditto, guitarist Brace Paine and drummer Kathy Mendonca while attending Evergreen State College in Olympia, Washington.[1&...

German aeronautical engineer, a pioneer of aerodynamics This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Alexander Lippisch – news · newspapers · books · scholar · JSTOR (November 2015) (Learn how and when to remove this template message) Alexander LippischAlexander Lippisch, with Günther Grönhoff in the co...

Australian rules footballer, born 1981 Australian rules footballer Brendan Fevola Fevola with the Brisbane Lions in January 2010Personal informationFull name Brendan FevolaNickname(s) Fev, The Shag, Fevalenko, The FevolutionDate of birth (1981-01-20) 20 January 1981 (age 42)Original team(s) Dandenong Stingrays (TAC Cup)Draft No. 38, 1998 National Draft, CarltonHeight 191 cm (6 ft 3 in)Weight 100 kg (220 lb)Position(s) ForwardPlaying career1Years Club Games (...

Cet article est une ébauche concernant une chanson et le Concours Eurovision de la chanson. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Would You? Single de Iris Sortie 2012 Durée 2:55 Langue Anglais Genre Pop Singles de Iris Wonderful(2011) Welcome to my world(2012)modifier Would You? (Voudrais-tu ?) est la chanson de l'artiste belge Iris qui représente la Belgique au Concours Eurovision de...



























