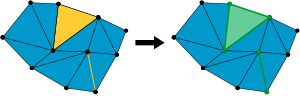
Simplizialkomplex
|
Read other articles:

?Яструб-крикун Яструб-крикун світлий (Melierax canorus) Біологічна класифікація Домен: Ядерні (Eukaryota) Царство: Тварини (Animalia) Тип: Хордові (Chordata) Інфратип: Хребетні (Vertebrata) Клас: Птахи (Aves) Ряд: Яструбоподібні (Accipitriformes) Родина: Яструбові (Accipitridae) Рід: Яструб-крикун (Melierax)G.R. Gray, 1840[1&#...

Ця стаття є сирим перекладом з англійської мови. Можливо, вона створена за допомогою машинного перекладу або перекладачем, який недостатньо володіє обома мовами. Будь ласка, допоможіть поліпшити переклад. (16 листопада 2019) Цаворит Гранат Цаворит на справжній матриці ср�...

1958 film by Jack Arnold The Space ChildrenTheatrical release posterDirected byJack ArnoldScreenplay byBernard C. SchoenfeldStory byTom FilerBased onThe Eggby Tom Filer[1]Produced byWilliam AllandStarring Michel Ray Adam Williams Peggy Webber Johnny Washbrook Jackie Coogan Richard Shannon CinematographyErnest LaszloEdited byTerry O. MorseMusic byVan CleaveColor processBlack and whiteProductioncompanyWilliam Alland Productions[2]Distributed byParamount PicturesRelease date June...

Hindu monk and teacher (1930–2015) This article is about the founder of the Arsha Vidya Gurukulam. For other uses, see Swami Dayananda (disambiguation). Swami Dayananda SaraswatiHis Holiness Swami Dayananda Saraswati, from the private collection of Arsha Vidya GurukulamPersonalBornNatarajan Gopala Iyer(1930-08-15)15 August 1930Manjakkudi, Tamil Nadu, IndiaDied23 September 2015(2015-09-23) (aged 85)Rishikesh, Uttarakhand, IndiaReligionHinduismNationalityIndianFounder ofArsha Vidya ...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2019年1月20日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 此條目需要精通或熟悉相关主题的编者参与及协助编辑。 (2019年1月20日)請邀請適合的人士改善本条目。更多的細節與詳情請參见討論頁。 此條...

Bagian dari seri mengenaiKelengkapan Heraldik Unsur-Unsur Lambang Kebesaran Perisai Bidang Penopang Jambul Bulang Hulu Mantel Ketopong Mahkota Lapik Perempat Semboyan (atau slogan) Lambang Kebesaran Hulu lbs Latar dalam heraldik adalah keseluruhan permukaan perisai dalam gambar lambang kebesaran. Latar biasanya dilapisi dengan satu atau lebih pulasan (warna, logam, atau kulit bulu). Latar dapat dibagi-bagi menjadi beberapa bidang, dan dapat pula dihiasi dengan pola berwarna-warni. Dalam segel...

American poet (born 1972) Staceyann ChinBorn (1972-12-25) December 25, 1972 (age 50)Spanish Town, JamaicaOccupation(s)Poet, writer, performance artist Staceyann Chin (born December 25, 1972) is a spoken-word poet, performing artist and LGBT rights political activist. Her work has been published in The New York Times, The Washington Post, and the Pittsburgh Daily, and has been featured on 60 Minutes. She was also featured on The Oprah Winfrey Show, where she shared her struggles growing u...

22e cérémonie des Goyas Prix Goya Organisé par l'Academia de las artes y las ciencias cinematográficas de España Détails Date 3 février 2008 Lieu Madrid Espagne Présentateur José Corbacho Site web http://www.academiadecine.com/ Résumé Meilleur film La soledad Meilleur réalisateur Jaime RosalesLa soledad Film le plus nommé Las 13 rosas (14) Film le plus récompensé L'Orphelinat (7) Chronologie 21e cérémonie des Goyas 23e cérémonie des Goyas modifier La 22...

Elisabeth VrbaVrba pada 2009Lahir(1942-05-17)17 Mei 1942Hamburg, JermanKebangsaanAmerika SerikatAlmamaterUniversitas Cape TownKarier ilmiahBidangPaleontologiInstitusiUniversitas Yale Elisabeth S. Vrba (lahir 17 Mei 1942) adalah seorang pakar paleontologi di Universitas Yale. Vrba meraih gelar Doktor dalam bidang Zoologi dan Palaeontologi di Universitas Cape Town, pada 1974. Daftar pustaka Gould, S. J. and E. S. Vrba. (1982). Exaptation—a missing term in the science of form. Paleobiology 8: ...

Estonian artist Meeli Kõiva Meeli Kõiva (known professionally as Mery Crystal Ra;[1] born 14 January 1960, Tartu, Estonia) is an Estonian-American artist, curator, and art filmmaker who primarily works with architectural glass, light and multimedia. She is active in Finland, Belgium, and the United States, where she has produced a range of paintings, architectural lighting sculptures, multimedia installations, videos, and architectural stained glass. She pioneered a new era of archi...

Historic house in New York State, USA Dykmans' home, Boscobel, on the Hudson River in New York state States Dyckman was an American Loyalist during the American Revolution who lived in New York state. A descendant of early Dutch settlers of New Amsterdam, he proved to be a man of both questionable ethics and allegiances. He somehow was able to retain his family fortune despite being an active Loyalist and working in the British Army's Quartermaster Corps for most of the war, keeping the accou...

?†Seitaad ruessiЧас існування: рання юра184 млн років тому Реконструкція скелету (білим кольором зображені відомі елементи) Біологічна класифікація Домен: Ядерні (Eukaryota) Царство: Тварини (Animalia) Тип: Хордові (Chordata) Клас: Плазуни (Reptilia) Надряд: † Динозаври (Dinosauria) Ряд: † Ящеротаз...

2001 treaty on plant genetic resources Plant TreatyInternational Treaty on Plant Genetic Resources for Food and AgricultureSigned2001LocationRome[1]Effective29 June 2004Parties147 contracting parties (146 states, 1 organization) as of 1 February 2020DepositarySecretary-General of the United NationsLanguagesArabic, Chinese, English, French, Russian and Spanish Rights Theoretical distinctions Claim rights and liberty rights Individual and group rights Natural rights and legal rights Neg...

German television channel Television channel WeltCountryGermanyBroadcast areaGermanyAustriaSwitzerlandHeadquartersBerlin, GermanyProgrammingPicture format1080i HDTV(downscaled to 16:9 576i for the SDTV feed)OwnershipOwnerWeltN24 GmbHSister channelsN24 DokuBildHistoryLaunched24 January 2000 (2000-01-24)Former namesN24 (2000–2018)LinksWebsitewelt.deAvailabilityTerrestrialDigital terrestrial televisionChannel slots vary depending on location (HD)Streaming median24.dewelt.de Logo...

1869 painting by George P.A. Healy Abraham LincolnArtistGeorge Peter Alexander HealyYear1869MediumOil on canvasDimensions187.3 cm × 141.3 cm (73.7 in × 55.6 in)LocationState Dining Room, White House, Washington, D.C. Abraham Lincoln is an 1869 oil-on-canvas painting by George Peter Alexander Healy of Abraham Lincoln, the 16th president of the United States. In the painting, a contemplative Lincoln is observed alone, leaning forward in a chair, with ...

2022 video game 2022 video gameSol CrestaDeveloper(s)PlatinumGamesPublisher(s)PlatinumGamesDirector(s)Takanori SatoHideki KamiyaProducer(s)Takahito WashisakaYuji NakaoDesigner(s)Hiromu NakazonoComposer(s)Yuzo KoshiroSeriesCresta SeriesNeo-Classic ArcadeEngineUnityPlatform(s)WindowsSwitchPlayStation 4ReleaseFebruary 22, 2022Genre(s)Scrolling shooterMode(s)Single-player Sol Cresta[a] is a vertically scrolling shooter video game developed and published by PlatinumGames.[1] It is ...

American civil rights law This article is about the 1957 Civil Rights Act. For other American laws called Civil Rights Acts, see Civil Rights Act. Civil Rights Act of 1957Long titleAn Act to provide means of further securing and protecting the civil rights of persons within the jurisdiction of the United States.Enacted bythe 85th United States CongressEffectiveSeptember 9, 1957CitationsPublic law85-315Statutes at Large71 Stat. 634Legislative historyIntroduced in the House as H....

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Polo pony – news · newspapers · books · scholar · JSTOR (March 2011) (Learn how and when to remove this template message) A polo pony A polo pony is the term used for a horse used in the game of polo. They may be of any breed or combination of breeds, though ma...

دراسة مريم العذراء والقط معلومات فنية الفنان ليوناردو دافنشي تاريخ إنشاء العمل 1478-1481 الموقع المتحف البريطاني الموضوع وسيط property غير متوفر. المتحف المتحف البريطاني المدينة لندن معلومات أخرى المواد حبر، وواضح [لغات أخرى]، وورق (سطح اللوحة الفنية) الأب�...

В Википедии есть статьи о других людях с такой фамилией, см. Селезнёв. Евгений Селезнёв Общая информация Полное имя Евгений Александрович Селезнёв Родился 20 июля 1985(1985-07-20)[1][2][…] (38 лет)Макеевка, Донецкая область, Украинская ССР, СССР Гражданство Украина Рост 188...