Quantengeometrie
|
Read other articles:

Sekolah VianneyInformasiDidirikan1995JenisSwastaKurikulumKurikulum 2013 dan Kurikulum MerdekaStatusSekolah Standar NasionalAlamatLokasiJl. Bojong Raya No. 98 Rawa Buaya Cengkareng, Jakarta Barat, DKI Jakarta, IndonesiaTel./Faks.021-5814170, 5806078/ 021-5814283Situs webvianney.sch.idMotoMotoVINCE IN BONO MALUM (Kalahkan kejahatan dengan kebaikan) Roma 12:21 Sejarah Nama sekolah Vianney diambil dari nama orang suci Santo Yohannes Maria Vianney. Tokoh ini dipilih sebagai pelindung sekolah,...

Spanish television network Television channel AtreseriesCountrySpain, Andorra, Gibraltar and PortugalProgrammingLanguage(s)SpanishOwnershipOwnerAtresmediaSister channelsAntena 3 LaSexta Neox Nova MegaHistoryLaunchedDecember 22, 2015 (2015-12-22)LinksWebsiteatreseries.atresmedia.comAvailabilityStreaming mediaAtresplayerLive Atreseries is a Spanish television channel owned by Atresmedia which was released on 22 December 2015.[1][2] Atreseries release historical TV...

Kontinentale Hockey-Liga ◄ vorherige Saison 2019/20 nächste ► Meister: abgebrochen • KHL | Wysschaja Hockey-Liga ↓ | Perwaja Liga ↓↓ Die Saison 2019/20 war die zwölfte Spielzeit der Kontinentalen Hockey-Liga, einer multinationalen Eishockeyliga. Titelverteidiger war der HK ZSKA Moskau. Die Liga startete mit 24 Mannschaften in die Saison, diese stammten aus Kasachstan, Lettland, Russland, Finnland, Belarus und China. Aufgrund der COVID-...

Station Herrera Station Herrera bij nacht Plaats San Sebastian Opening 18 oktober 1863 Perronsporen 2 Lijn(en) Spoorlijn Madrid-Hendaye Eigendom ADIF Vervoerder(s) Renfe Lijnen Trein Cercanías San Sebastian Bus Stadsbussen Metro Metro van San Sebastian Locatie Coördinaten 43° 19′ NB, 1° 56′ WL Portaal Openbaar vervoer Spanje Station Herrera is een spoorweghalte in de wijk Herrera, in het district Altza van de Spaanse stad San Sebastian, in de autonome gemeen...

Kedutaan Besar India, JakartaKoordinat6°12′54″S 106°48′50″E / 6.214982°S 106.813797°E / -6.214982; 106.813797AlamatGama Tower, 28th floor, Jl. HR. Rasuna Said Kav. C22, Karet Kuningan, Setiabudi, Kota Jakarta Selatan, Jakarta 12940.Duta BesarSandeep ChakravortyYurisdiksi Indonesia Timor LesteSitus webSitus web resmi Kedutaan Besar India di Jakarta adalah misi diplomatik India ke Jakarta, yang sekaligus juga terakreditasi untuk Timor Timur.[1&#...

■ wintertijd noordelijk halfrond ■ wintertijd zuidelijk halfrond/zomertijd noordelijk halfrond ■ aan land, gehele jaar ■ op zee, gehele jaar UTC+1 is de tijdzone voor: Midden-Europese Tijd (MET) West-Afrikaanse Tijd (WAT) Britse Zomertijd of Ierse Zomertijd (in Ierland) of West-Europese Zomertijd (in Portugal en op de Canarische Eilanden) Landen met zomertijd Landen en gebieden met zomertijd zijn op het noordelijk halfrond (*) of het zuidelijk halfrond (**): Albani...

Craig MacLean Craig MacLean (2019) Zur Person Geburtsdatum 31. Juli 1971 Nation Vereinigtes Konigreich Vereinigtes Königreich Disziplin Bahn (Kurzzeit) / Paracycling Wichtigste Erfolge Olympische Spiele 2000 – Sprint UCI-Bahn-Weltmeisterschaften 2002 – Teamsprint Commonwealth Games 2006 – Teamsprint UCI-Paracycling-Bahnweltmeisterschaften 2011, 2012 – Sprint, Zeitfahren Letzte Aktualisierung: 19. Dezember 2022 Craig MacLean (* 31. Juli 1971 in Grantown-on-Spey) ist ein scho...

Claire McCaskill Claire Conner McCaskill (/məˈkæskəl/; lahir 24 Juli 1953) adalah seorang politikus Amerika Serikat yang menjabat sebagai Senator Amerika Serikat dari Missouri dari 2007 sampai 2019 dan sebagai Auditor Negara Bagian Missouri dari 1999 sampai 2007. McCaskill berasal dari Rolla, Missouri. Pranala luar Wikisumber memiliki karya asli dari atau mengenai: Claire McCaskill Wikimedia Commons memiliki media mengenai Claire McCaskill. Claire McCaskill di Curlie (dari DMOZ) Kemuncula...

Indian actor In this Indian name, the name Rajkumar is a patronymic, and the person should be referred to by the given name, Raghavendra. Raghavendra RajkumarRaghavendra in 2010Born (1965-08-15) 15 August 1965 (age 58)Madras, Madras State (now in Tamil Nadu), IndiaOther namesRaganna[1]Occupation(s)Actor, dancer, film producerYears active1974–presentSpouseMangalaChildren2 (including Vinay Rajkumar)Parent(s)Dr. Rajkumar (father)Parvathamma (mother)RelativesSee Rajkumar ...

Indian mathematician Dinesh ThakurBorn1961IndiaAlma materHarvard University University of BombayScientific careerFieldsMathematicsInstitutionsUniversity of RochesterDoctoral advisorJohn Tate Dinesh S. Thakur is an Indian mathematician and a professor of mathematics at University of Rochester.[1] Before moving to Rochester, Thakur was a professor at University of Arizona.[2] His main research interest is number theory. Early life Thakur was born in Mumbai, India. He attend...

United States labor law of the New Frontier program The Equal Pay Act of 1963Acronyms (colloquial)EPAEnacted bythe 88th United States CongressCitationsPublic lawPub. L.Tooltip Public Law (United States) 88–38Statutes at Large77 Stat. 56CodificationActs amendedFair Labor Standards ActTitles amended29U.S.C. sections amended206Legislative historyIntroduced in the Senate as S. 1409 by Patrick McNamara (D–MI)[1][2]Signed into law by President John F. Ke...

American anthropologist This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Jules Henry – news · newspapers · books · scholar · JSTOR (September 2020) (Learn how and when to remove this template message) Jules Henry (November 29, 1904 – September 23, 1969) was an American anthropologist. After studies at t...

Higher-education institution in Paris, France Paris Institute of Political StudiesInstitut d'études politiques de Paris (French)Other nameSciences PoFormer nameÉcole libre des sciences politiquesMottoFrench: Aux racines de l'avenirMotto in EnglishRoots of the FutureTypePublic research universityGrande école[1]Grand établissementInstitut d'études politiquesEstablished1872; 151 years ago (1872)FounderÉmile BoutmyEndowment€127.2 million (2018)[2]Bud...

Band For other uses of the term, see Magic number (disambiguation). The Magic NumbersBackground informationOriginEaling, LondonGenresAlternative rock, indie rockYears active2002–presentLabelsCapitol Records/EMI, Heavenly, Caroline International, Role Play RecordsMembersAngela GannonSean GannonMichele StodartRomeo Stodart The Magic Numbers are an English alternative rock band consisting of two brother-and-sister pairs, from Hanwell in west London. The group was formed in 2002, releasing thei...

369.º Regimiento Croata de Infantería ReforzadaLegión Croata Verstärktes Kroatisches Infanterie-Regiment 369 369. pojačana pješačka pukovnija Activa 16 de julio de 1941 - enero de 1943País Tercer ReichRama/s WehrmachtTipo InfanteríaTamaño Regimiento (4.500 aprox.)Disolución 1943Alto mandoComandantesnotables Ivan Markulj, Viktor Pavičić, Marko Mesić, Ivan Babić, Tahir AlagićInsigniasInsignia Bandera Cultura e historiaMote «Legión Croata»Lema Što Bog da i sreća junačka! (�...

Yunani padaOlimpiade Musim Dingin 2010Kode IOCGREKONKomite Olimpiade YunaniSitus webwww.hoc.gr (dalam bahasa Yunani)Penampilan pada Olimpiade Musim Dingin 2010 di VancouverPeserta7 dalam 3 cabang olahragaPembawa benderaThanassis TsakirisMedali 0 0 0 Total 0 Penampilan pada Olimpiade Musim Dingin (ringkasan)193619481952195619601964196819721976198019841988199219941998200220062010201420182022 Yunani ikut serta dalam Olimpiade Musim Dingin 2010 in Vancouver, British Columbia, ...

Indian cinematographer In this Indian name, the name Gangadharan is a patronymic, and the person should be referred to by the given name, Girish. Girish GangadharanBorn (1985-03-08) 8 March 1985 (age 38)Chadayamangalam, Kollam, Kerala, IndiaOccupationDirector of PhotographyYears active2013–presentSpouseShyna Girish Gangadharan ISC (born 8 March 1985) is an Indian cinematographer known for his work in Malayalam and Tamil films. He is the recipient of the National Film Award for Bes...

A questa voce o sezione va aggiunto il template sinottico {{Scuola}} Puoi aggiungere e riempire il template secondo le istruzioni e poi rimuovere questo avviso. Se non sei in grado di riempirlo in buona parte, non fare nulla; non inserire template vuoti. L'edificio Mochkin, entrata principale della scuola elementare della Yeshivah. Yeshivas Oholei Yosef Yitzchok Lubavitch, comunemente noto e chiamato Yeshivah College - in italiano: Collegio Yeshivah - è una scuola indipen...
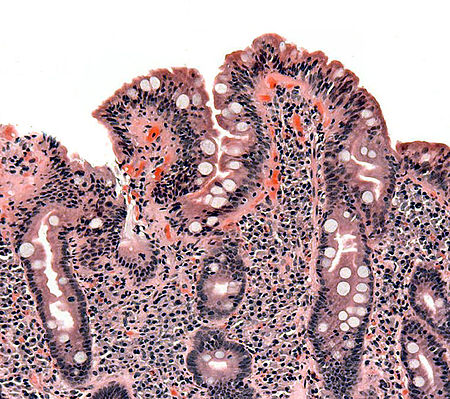
Penyakit seliakBiopsi dari usus halus yang menunjukkan penyakit seliak yang dapat dilihat dengan menumpulkan villus usus,hipertrofi crypt, dan limfosit infiltrasi cryptsInformasi umumPelafalan/ˈsiːliæk/ see-LEE-akSpesialisasiGastroenterologi, obat penyakit dalamPenyebabReaksi terhadap gluten[1]Aspek klinisGejala dan tandaTidak ada atau non-specific, distensi abdomen, diare, konstipasi, malabsorption, penurunan berat badan, dermatitis herpetiformis[2][3]KomplikasiAne...

United States v. WindsorMahkamah Agung Amerika SerikatDisidangkan pada 27 Maret, 2013Diputus pada 26 Juni, 2013Nama lengkap kasusUnited States, Petitioner v. Edith Schlain Windsor, in Her Capacity as Executor of the Estate of Thea Clara Spyer, et al.Docket nos.12-307Kutipan570 U.S. ___ (lanjut)Versi sebelumnyaDOMA dinyatakan tidak konstitusional sub. nom. Windsor v. United States, 833 F. Supp. 2d 394 (S.D.N.Y. 2012); Affirmed, 699 F.3d 169 (2d Cir. 2012)ArgumenOral argumentOpinion Announcment...
