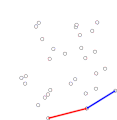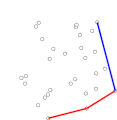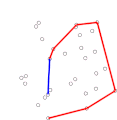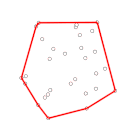
Konvexe Hülle
|
Read other articles:

Palacio de Queluz Monumento nacional de Portugal La fachada principal y Cuerpo Central del Palacio de QueluzLocalizaciónPaís PortugalLocalidad QueluzUbicación Queluz e BelasCoordenadas 38°45′02″N 9°15′30″O / 38.750446, -9.258224Información generalUsos Museo y residencia de jefes de Estado extranjeros.Estilo Barroco, Rococó, NeoclásicoInicio 1747Finalización 1786Remodelación 1934-1940Propietario Estado portugués (desde 1908), anteriormente: Casa de Braganza (...

سيد عبد الله (ممثل) سيد عبد الله حافظ (الشهير بسيد عبد الله) (بالإنجليزية: Sayed Abdallah Hafez)[1][2] ممثل مصري من مواليد عشرينات القرن الماضي وتوفي في السبعينات،[3] مسيرته السينمائية بدأت أوائل خمسينات القرن 20، واستمر يؤدي الأدوار الصغيرة في السينما حتى النصف الأول من

Leonora von Ottinger Información personalNacionalidad EstadounidenseLengua materna Inglés Información profesionalOcupación Actriz de cineActriz de teatro[editar datos en Wikidata] Leonora von Ottinger fue una actriz estadounidense que trabajó en películas mudas y en obras teatrales. Protagonizó 16 películas y principalmente trabajó en la industria teatral. En Broadway, von Ottinger apareció en The Melting Pot (1909).[1] Apareció juntó con William Garwood en ...

Sportart Biathlon Disziplin Staffel Geschlecht Mixed Teilnehmer 160 Athleten aus 20 Ländern Wettkampfort Laura Biathlon- und Skilanglaufzentrum Wettkampfphase 19. Februar 2014 Siegerzeit 1:09:17,0 h Medaillengewinner Norwegen Norwegen Tora Berger, Tiril Eckhoff, Ole Einar Bjørndalen, Emil Hegle Svendsen Tschechien Tschechien Veronika Vítková, Gabriela Soukalová, Jaroslav Soukup, Ondřej Moravec Italien Italien Dorothea Wierer, Karin Oberhofer, Dominik Windisch, Lukas Hofer...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مارس 2020) تلال الذهب في الربيع. تلول الذهب، الواقعة في الأردن، وهما تلان متجاورتان في وادي نهر الزرقاء، على بعد ساعة بالسيارة شمال غرب العاصمة الأردنية عمان. غرب التلان...

American mathematician William BrowderBorn (1934-01-06) January 6, 1934 (age 89)New York City, USEducationMassachusetts Institute of Technology (BS)Princeton University (MS, PhD)Known forSurgery theory method for classifying high-dimensional manifoldsParentEarl Browder (father)RelativesFelix Browder (brother)Andrew Browder (brother)Bill Browder (nephew)Joshua Browder (great-nephew)Scientific careerFieldsMathematicsInstitutionsPrinceton UniversityDoctoral advisorJohn Coleman MooreDoc...

Fort de Pierre-LevéeL'entrée du fort de Pierre-Levée, vue de l'intérieurPrésentationType FortPropriétaire ÉtatPatrimonialité Inscrit MH (1984)LocalisationPays FranceRégion Pays de la LoireDépartement VendéeCommune L'Île-d'YeuCoordonnées 46° 43′ 09,28″ N, 2° 21′ 31,77″ OLocalisation sur la carte de la VendéeLocalisation sur la carte de Francemodifier - modifier le code - modifier Wikidata Le fort de Pierre-Levée (mieux connu loc...

Japanese light novel series and its franchise My Happy MarriageFirst light novel volume cover, featuring Miyo Saimori (left) and Kiyoka Kudou (right)わたしの幸せな結婚(Watashi no Shiawase na Kekkon)GenreFantasy[1] Novel seriesWritten byAkumi AgitogiPublished byShōsetsuka ni Narō Light novelWritten byAkumi AgitogiIllustrated byTsukiho TsukiokaPublished byFujimi ShoboEnglish publisherNA: Yen PressImprintFujimi L BunkoDemographicFemaleOriginal runJanua...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2016. Seni tari Suku Kutai dapat dibagi menjadi 2 jenis, yakni seni tari rakyat dan seni tari klasik.[1] Seni Tari Rakyat Seni Tari Rakyat Merupakan Kreasi artistik yang timbul ditengah-tengah masyarakat umum.[1] Gerakan tarian rakyat ini mengg...

The Deputy Chief Minister of Odisha is a member of the Cabinet of Odisha Government in the Government of Odisha. Not a constitutional office, it seldom carries any specific powers.[1] A deputy chief minister usually also holds a cabinet portfolio such as home minister or finance minister. In the parliamentary system of government, the Chief Minister is treated as the first among equals in the cabinet; the position of deputy chief minister is used to bring political stability and stren...

Single turn or loop of yarn This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (December 2021) (Learn how and when to remove this template message) Hand-stitches In the textile arts, a stitch is a single turn or loop of thread, or yarn. Stitches are the fundamental elements of sewing, knitting, embroidery, crochet, and needle lace-making, whether by hand or machi...

Restaurant in Dhaka, BangladeshHaji biryaniRestaurant informationEstablished1939; 84 years ago (1939)Owner(s)Haji Mohammad ShahedPrevious owner(s)Haji Mohammad Hossain, Haji Mohammad Golam HossainFood typeChevon (goat's meat) biryaniStreet address70 Kazi Alauddin Road, Nazira BazarCityDhakaCountryBangladeshSeating capacity50Other locationsMotijheel Haji biryani (also known as Hajir biryani) is one of the oldest restaurants in the heart of Old Dhaka, Bangladesh, selling chevo...

Naked ScienceNaratorBervariasiNegara asalASProduksiDurasi1 jamRilis asliJaringanNational GeographicRilis2004 –2011 Naked Science adalah sebuah acara yang ditayangkan dari National Geographic Channel. Acara tersebut menyediakan jawaban atas pertanyaan-pertanyaan ilmu pengetahuan yang rumit. Naked Science tidak berhubungan dengan Naked Scientists dari Britania Raya yang berdiri tahun 2001 atau dengan situs web NakedScience.com. Episode Musim 1 (2004) Asteroid Mematikan Gunung Berapi Supe...

Musée départemental Georges-de-La-TourMusée départemental Georges-de-La-Tour (à gauche)Informations généralesType Musée d'artOuverture 2003Surface 960 m2Visiteurs par an 7 176 (2018)Site web www.mosellepassion.fr/index.php/les-sites-moselle-passion/musee-georges-de-la-tourCollectionsÉpoque XVIIe siècle - XXe siècleLocalisationPays FranceCommune Vic-sur-SeilleAdresse Parc Naturel Régional de Lorraine, Place Jeanne d'Arc, 57630 Vic-sur-SeilleCoordonnées 48...

1990 single by Miho Nakayama Midnight TaxiSingle by Miho Nakayamafrom the album All for You LanguageJapaneseB-sideHonki Demo...ReleasedJanuary 15, 1990 (1990-01-15)Recorded1989GenreJ-popLength4:53LabelKing RecordsComposer(s)Ryō AsukaLyricist(s)Ryo AsukaMiho Nakayama singles chronology Rosécolor (1989) Midnight Taxi (1990) Semi-sweet Magic (1990) Midnight Taxi (ミッドナイト・タクシー, Middonaito Takushī) is the 17th single by Japanese entertainer Miho Nakayama. Wri...

Disease caused by the bacteria Salmonella Typhi Not to be confused with Typhus. Medical conditionTyphoid feverOther namesEnteric fever, slow feverCausative agent: Salmonella enterica serological variant Typhi (shown under a microscope with flagellar stain)SpecialtyInfectious diseases SymptomsFever that starts low and increases daily, possibly reaching as high as 104.9 °F (40.5 °C) Headache, weakness and fatigue, muscle aches, sweating, dry cough, loss of appetite, weight loss, stomach ...

Канализационный люк над смотровым колодцем — сооружение для доступа к подземным коммуникациям, таким, как сточная, ливневая, кабельная или трубопроводная канализация. Содержание 1 Разновидности 1.1 Выпускаются 1.1.1 По конструкции 1.1.2 По материалу 2 Устройство колодцев 2...

Division of the BBC for Wales BBC Cymru WalesBBC Cymru Wales' area within the UKTV stationsBBC One WalesBBC Two WalesTV transmittersBlaenplwyfCarmelLlanddonaMoel-y-ParcPreseliPrestatynWenvoeRadio stationsBBC Radio WalesBBC Radio CymruBBC Radio Cymru 2HeadquartersNew Broadcasting House, CardiffAreaWalesOwnerBBCBBC StudiosKey peopleRhuanedd Richards (Director of BBC Cymru Wales)Launch date9 February 1964; 59 years ago (1964-02-09)Official websitebbc.co.uk/walesLanguageEnglish ...

Dominican kids playing Plaquita, a baseball-like game. The Dominican Republic has some traditional games. Traditional games El juego del pañuelo El juego del pañuelo is a game similar to steal the bacon.[1] Hoyito Hoyito is a mancala game.[2] Plaquita Plaquita is a game with similarities to street cricket.[3][4] Vitilla Vitilla is a type of street baseball in which a plastic water bottle cap and a broomstick replace the baseball and bat respectively.[5 ...

Museo dell'orsoTeca in cui è esposto un esemplare imbalsamato di orso bruno marsicano UbicazioneStato Italia LocalitàGagliano Aterno Indirizzopiazza del Municipio Coordinate42°07′34.04″N 13°42′01.06″E / 42.126123°N 13.700295°E42.126123; 13.700295Coordinate: 42°07′34.04″N 13°42′01.06″E / 42.126123°N 13.700295°E42.126123; 13.700295 CaratteristicheTipoNaturalistico GestioneCorpo forestale dello Stato Sito web Modifica dati su Wikidat...