Backtracking
|
Read other articles:

ТелевидениеЛоготип порталаИстория Телевидение в США Телевидение в России Телевидение в СССР Термины Телевизионная сеть Телевизионная синдикация Апфронт Телефильм Рейтинг Нильсена Замена в середине сезона Премьера сезона Премьера сериала Финал сезона Финал сериала �...

Río Cañas redirects here. For other uses, see Río Cañas (disambiguation). River of Puerto Rico Cañas RiverCañas River in Ponce, Puerto Rico, crossing through Hacienda Buena VistaLocationCommonwealthPuerto RicoMunicipalityPoncePhysical characteristicsSource • locationCerro Avispa, Barrio Guaraguao • coordinates18°00′07″N 66°38′26″W / 18.0019106°N 66.6404508°W / 18.0019106; -66.6404508[1] •&#...

Liga Champions beralih ke halaman ini. Untuk kegunaan lain, lihat Liga Champions (disambiguasi). Liga Champions UEFAMulai digelar1955; 68 tahun lalu (1955)(menggunakan format terkini sejak 1992)WilayahEropa (UEFA)Jumlah tim32 (babak penyisihan grup)79, 80 atau 81 (total)Kualifikasi untukPiala Super UEFAPiala Dunia Antarklub FIFAKompetisi terkaitLiga Eropa UEFA (tingkat ke 2)Liga Konferensi Eropa UEFA (tingkat ke 3)Juara bertahan Manchester City (gelar ke-1)Tim tersukses Real Madrid (14 g...

American basketball player Rashad BellBell in 2018DeanPositionForwardPersonal informationBorn (1982-09-23) September 23, 1982 (age 41)New York City, New YorkNationalityAmerican / HungarianListed height6 ft 8 in (2.03 m)Listed weight212 lb (96 kg)Career informationHigh schoolSt. Francis Prep(Queens, New York)CollegeBoston University (2001–2005)NBA draft2005: undraftedPlaying career2005–presentCareer history2005–2006Basket Porvo2006Long Island PrimeTime2006�...

U.S. political event held in Chicago, Illinois 1892 Democratic National Convention1892 presidential election Nominees Cleveland and StevensonConventionDate(s)June 21–23, 1892CityChicago, IllinoisVenueThe WigwamCandidatesPresidential nomineeGrover Cleveland of New YorkVice presidential nomineeAdlai E. Stevenson of Illinois‹ 1888 · 1896 › The 1892 Democratic National Convention was held in Chicago, Illinois, June 21–June 23, and nominated former President Grover Cle...

Book by Robert I. Sutton AuthorRobert I. SuttonGenreBusinessPublisherBusiness PlusPublication dateFebruary 22, 2007Pages224ISBN978-0-446-52656-2OCLC154698708Dewey Decimal650.1/3 22LC ClassHD58.7 .S935 2007The No Asshole Rule: Building a Civilized Workplace and Surviving One That Isn't is a book by Stanford professor Robert I. Sutton. He initially wrote an essay[1] for the Harvard Business Review, published in the breakthrough ideas for 2004. Following the essay, he received more ...
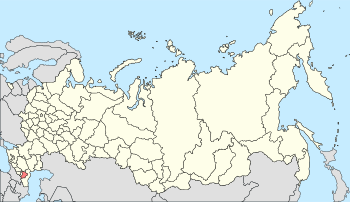
Location of the Chechen Republic in Russia Location of the Republic of Ingushetia in Russia Sunzhunsky District is the name of several administrative and municipal districts in Russia: Sunzhensky District, Chechen Republic, an administrative[1] and municipal[2] district of the Chechen Republic Sunzhensky District, Republic of Ingushetia, an administrative and municipal[3] district of the Republic of Ingushetia Sunzhensky otdel, a former district of the Russian Empire S...

Bistum Troyes Karte Bistum Troyes Basisdaten Staat Frankreich Kirchenprovinz Reims Metropolitanbistum Erzbistum Reims Diözesanbischof Alexandre Joly Emeritierter Diözesanbischof Marc Stenger Fläche 6004 km² Pfarreien 43 (2017 / AP 2018) Einwohner 315.000 (2017 / AP 2018) Katholiken 219.518 (2017 / AP 2018) Anteil 69,7 % Diözesanpriester 51 (2017 / AP 2018) Ordenspriester 16 (2017 / AP 2018) Katholiken je Priester 3276 Ständige Diakone 24 (2017 / AP 2018) Ordensbrüder 19 (2017 / AP...

Ethnic group in India Kodava Coat of Arms[citation needed] KodavaTotal population(approx) 160,000Regions with significant populationsKodagu, Bangalore, MysoreLanguagesKodava takkReligionHinduismRelated ethnic groupsKannada people, Tulu People, Malayali people[1] Part of a series on theCulture of KarnatakaEmblem of Karnataka History Political history of medieval Karnataka Unification of Karnataka Etymology Historical sites of North Karnataka Alupa dynasty. Kadamba dynasty. Chal...

Indian racing driver and entrepreneur Anindith ReddyEducationMechanical EngineeringKnown forRacingSpouseShriya BhupalParentsKonda Vishweshwar Reddy (father)Sangita Reddy (mother)RelativesPrathap C. Reddy (grandfather) Anindith Reddy is an Indian racing driver.[1] He participated in the 2016 Euro JK 16 Championship and the Euro JK 2017 Championship,[2][3] and the motorsport person of the year 2017 at the Federation of Motorsports Clubs of India (FMSCI).[4] ...

Syndicat de la fonction publique et parapublique du Québec Cadre Forme juridique Syndicat Zone d’influence Québec Fondation Fondation 1962 Identité Président Christian Daigle Affiliation internationale Internationale des services publics Membres 40 000 Représentativité Fonction publique du Québec modifier Le Syndicat de la fonction publique et parapublique du Québec (SFPQ) est une organisation syndicale indépendante qui représente principalement les fonctionnaires de l'État ...

2014 studio album by Wadada Leo Smith, Jamie Saft, Joe Morris and Balázs PándiRed HillStudio album by Wadada Leo Smith, Jamie Saft, Joe Morris and Balázs PándiReleasedSeptember 23, 2014Recorded2014StudioPotterville International Studios, NYGenreJazzLength66:29LabelRareNoise RNR044ProducerJamie Saft, Joe MorrisWadada Leo Smith chronology Sonic Rivers(2014) Red Hill(2014) The Great Lakes Suites(2014) Jamie Saft chronology The New Standard(2014) Red Hill(2014) Ticonderoga(2015) Red H...

Drøsselbjerg Parochie van Denemarken Situering Bisdom Bisdom Roskilde Gemeente Kalundborg Coördinaten 55°28'21,11NB, 11°12'42,52OL Algemeen Inwoners (2004) 564 Leden Volkskerk (2004) 489 Overig Kerken Drøsselbjerg Kirke Proosdij Kalundborg Provsti Pastoraat Kirke Helsinge-Drøsselbjerg Foto's Kerk Portaal Denemarken Drøsselbjerg is een parochie van de Deense Volkskerk in de Deense gemeente Kalundborg. De parochie maakt deel uit van het bisdom Roskilde en telt 489 kerkleden ...

Ajude a melhorar este artigo sobre Arquitetura ilustrando-o com uma imagem. Consulte Política de imagens e Como usar imagens. Nota: Este artigo é sobre o templo no Concelho de Vila do Bispo. Para outros edifícios com este nome, veja Ermida de Santo António. Ermida de Santo António Religião Igreja Católica Romana Diocese Diocese do Algarve Geografia País Portugal Região Distrito de Faro Local Concelho de Vila do Bispo A Ermida de Santo António é um edifício religios...

Religious zionist leader (1891–1982) RabbiZvi Yehuda Kook הרב צבי יהודה קוקPersonalBorn23 April 1891ŽeimelisDied9 March 1982(1982-03-09) (aged 90)JerusalemReligionJudaismNationalityIsraeliSpouseChava Leah HutnerParent(s)Abraham Isaac and Reiza Rivka KookDenominationOrthodoxPositionRosh yeshivaYeshivaMercaz HaRavBegan1952Ended1982BuriedMount of Olives Jewish Cemetery, Jerusalem Zvi Yehuda Kook (Hebrew: צבי יהודה קוק, 23 April 1891 – 9 March 1982) was a promin...

2015 film The Chosen OnesFilm posterDirected byDavid PablosRelease dates 18 May 2015 (2015-05-18) (Cannes) 22 April 2016 (2016-04-22) (Mexico) Running time105 minutesCountryMexicoLanguageSpanish The Chosen Ones (Spanish: Las elegidas) is a 2015 Mexican drama film directed by David Pablos. It was screened in the Un Certain Regard section at the 2015 Cannes Film Festival.[1][2] The film was named on the shortlist for Mexico's entry for the A...

Set of sports originating, and mainly played in Ireland For the video games, see Gaelic Games (series). Gaelic games are present across the world. This sign in Sorrento, Italy, advertises that Gaelic games are shown in the bar. Gaelic games (Irish: Cluichí Gaelacha) are a set of sports played worldwide, though they are particularly popular in Ireland, where they originated. They include Gaelic football, hurling, Gaelic handball and rounders. Football and hurling, the most popular of the spor...

Cet article est une ébauche concernant les Jeux olympiques et la Suisse. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Suisse aux Jeux olympiques d'été de 1960 Code CIO SUI Comité Comité olympique Suisse Lieu Rome Participation 14e aux Jeux d'été Athlètes 149 (147 hommes et 2 femmes) dans 16 disciplines Porte-drapeau August Hollenstein (tir) MédaillesRang : 24e Or0 Arg.3 Bron.3 Total6 Suisse aux J...

Comic book superhero team For other uses, see Illuminati (disambiguation). IlluminatiProminent members of the Illuminati (clockwise from left to right): Iron Man, Black Bolt, Doctor Strange, Mister Fantastic, Namor the Sub-Mariner and Professor X in artwork for the cover of New Avengers: Illuminati Vol 2 #1 (Feb, 2007). Art by Jimmy CheungPublication informationPublisherMarvel ComicsFirst appearanceNew Avengers #7 (July 2005)Created byBrian Michael Bendis (writer)Steve McNiven (artist)In-stor...

2010 single by PendulumThe IslandSingle by Pendulumfrom the album Immersion Released 19 September 2010 (digital) 20 September 2010 (CD) 8 November 2010 (vinyl) Recorded2009–2010Genre Progressive house electro house Length 9:30 Album versions:5:20 The Island – Pt. I (Dawn) 4:09 The Island – Pt. II (Dusk) Label Warner Music UK Earstorm Breakbeat Kaos Songwriter(s)Rob SwireProducer(s) Rob Swire Gareth McGrillen Pendulum singles chronology Witchcraft (2010) The Island (2010) Crush (2011) Th...














