Magnetizace (veličina)
|
Read other articles:

В Википедии есть статьи о других людях с фамилией Мочениго. Альвизе II Моченигоитал. Alvise II Mocenigo 110-й венецианский дож 17 июля 1700 — 6 марта 1709 Предшественник Сильвестро Вальер Преемник Джованни II Корнер Рождение 3 января 1628(1628-01-03)Венеция Смерть 6 марта 1709(1709-03-06) (81 год)Вен�...

Murumuru TaxonomíaSuperreino: EukaryotaReino: PlantaeDivisión: MagnoliophytaClase: LiliopsidaSubclase: CommelinidaeFamilia: ArecaceaeSubfamilia: ArecoideaeTribu: CocoseaeSubtribu: BactridinaeGénero: AstrocaryumEspecie: Astrocaryum murumuruMart. 1824Sinonimia Astrocaryum yauaperyense Barb.Rodr. [editar datos en Wikidata] Astrocaryum murumuru, conocida como murumuru, chontaloro, chechana, huilango, huicungo,[1] u orocorí, es una palmera de la familia Arecaceae, nativ...

この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。(2014年3月) 独自研究が含まれているおそれがあります。(2014年3月)出典検索?: シクストゥス5世 ローマ教皇 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · ND...

Chef opérateur du sonCodesROME (France) L1508modifier - modifier le code - modifier Wikidata Au cinéma et dans le film documentaire, le chef opérateur du son, ou ingénieur du son, (en anglais, sound mixer, production sound mixer, sound recordist...) est le responsable de la prise de son sur le tournage, travaillant en étroite collaboration avec son assistant, le perchman. Historique Les premiers enregistrements sonores sur les plateaux de cinéma étaient lourds et demandaient beaucoup d...

Ilustración esquemática de la denudación regional para cuerpos rocosos intrusivos alcalinos félsicos del Estado de Río de Janeiro: la isla de Cabo Frío y el macizo de Itaúna. En geología, la denudación comprende los procesos que provocan el desgaste de la superficie terrestre por el movimiento del agua, el hielo, el viento y las olas, lo que lleva a una reducción de la elevación y del relieve de las formas terrestres y de los paisajes. Procesos endógenos como los volcanes, los ter...
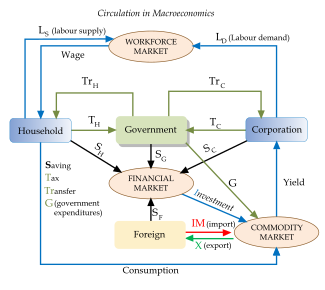
Sirkulasi Ekonomi Makro Ekonomi makro atau makroekonomi adalah studi tentang ekonomi secara keseluruhan.[1] Makroekonomi menjelaskan perubahan ekonomi yang mempengaruhi banyak masyarakat, perusahaan, dan pasar. Ekonomi makro dapat digunakan untuk menganalisis cara terbaik untuk memengaruhi target-target kebijaksanaan seperti pertumbuhan ekonomi, stabilitas harga, tenaga kerja dan pencapaian keseimbangan neraca yang berkesinambungan. Meskipun ekonomi makro merupakan bidang pembelajaran...

Iranian film director and screenwriter Asghar FarhadiFarhadi at the 2018 Stockholm International Film FestivalBorn (1972-05-07) 7 May 1972 (age 51)Homayoon Shahr, Isfahan, Pahlavi IranAlma materTarbiat Modares UniversityUniversity of TehranOccupationsFilm directorscreenwriterfilm producerYears active1997–presentNotable workAbout Elly (2009)A Separation (2011)The Past (2013)The Salesman (2016)Everybody Knows (2018)A Hero (2021)Spouse Parisa Bakhtavar (m. 19...

Russian stage and film actor (born 1980) Yuri KolokolnikovYuri Kolokolnikov, 2010BornYuri Andreyevich Kolokolnikov (1980-12-15) 15 December 1980 (age 42)Moscow, RSFSR, Soviet UnionNationalityRussianCitizenshipRussia and CanadaOccupation(s)Actor, film producerYears active1994–presentPartnerKseniya Rappoport (until 2014)Children2 Yuri Andreyevich Kolokolnikov (Russian: Юрий Андреевич Колокольников; born 15 December 1980) is a Russian stage and film actor.&#...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: TV HIT – news · newspapers · books · scholar · JSTOR (May 2017) (Learn how and when to remove this template message) Television channel TV HITCountryBosnia and HerzegovinaBroadcast areaBrčkoHeadquartersBrčko DistrictProgrammingLanguage(s)SerbianPicture format4:3 576i SDTVOwner...

Pour les articles homonymes, voir Arches. Parc national des ArchesSkyline Arch.GéographiePays États-UnisÉtat UtahComté comté de GrandCoordonnées 38° 43′ 41″ N, 109° 32′ 24″ OVille proche MoabSuperficie 354,2 km2Point culminant Elephant ButtePartie de Mighty FiveAdministrationNom local (en) Arches National ParkType Parc national des États-Unis, parc nationalCatégorie UICN II (parc national)WDPA 996Création 12 novembre 1971Patrimoniali...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (April 2023) Valentina KovaBornSaint Petersburg, RussiaNationalityAmericanEducationParsons The New School for DesignLabelValentina KovaAwardsRussian Woman of the YearWebsitehttps://valentinakova.com/ Valentina Kova is a Russian-American fashion designer and entrepreneur who co-founded her eponymous label in 2011 in New York City.[1&...
Parafia Świętego Antoniego kościół parafialny Państwo Polska Siedziba Kalna Adres ul. Kościelna 19543-376 Kalna Data powołania 2008 Wyznanie katolickie Kościół rzymskokatolicki Diecezja bielsko-żywiecka Dekanat Łodygowice Kościół św. Antoniego w Kalnej Proboszcz ks. Kazimierz Hanzlik Wezwanie św. Antoniego Wspomnienie liturgiczne 13 czerwca Położenie na mapie gminy BuczkowiceParafia Świętego Antoniego Położenie na mapie PolskiParafia Świętego Antoniego Położe...

De plaats Laag-Keppel, onderdeel van de gemeente Bronckhorst, kent 39 gemeentelijke monumenten: Object Bouwjaar Architect Locatie Coördinaten Nr. Afbeelding Wilhelminabruggetje 1898[1] Dorpsstraat 51° 59' 42 NB, 6° 13' 32 OL 1876/wikinr166 Wilhelminabruggetje Woonhuis/postkantoor/schuur Dorpsstraat 9 51° 59' 42 NB, 6° 13' 29 OL 1876/wikinr167 Woonhuis/postkantoor/schuur Woonhuis ca. 1905[1] Dorpsstraat 12 5...

Descendants 3Poster promosiGenre Musikal Fantasi Remaja Ditulis oleh Josann McGibbon Sara Parriott SutradaraKenny OrtegaPemeran Dove Cameron Cameron Boyce Sofia Carson Booboo Stewart Cheyenne Jackson China Anne McClain Penata musikDavid LawrenceNegara asalAmerika SerikatBahasa asliInggrisProduksiProduser eksekutif Kenny Ortega Josann McGibbon Sara Parriott Wendy Japhet ProduserWendy JaphetDurasi108 MenitRumah produksiDisney Channel Original ProductionsRilis asliJaringanDisney ChannelRil...

American reality television series The Pauly D ProjectGerard Big Jerry Gialanella, Jason JROC Craig, Paul Pauly D DelVecchio, Ryan Labbe and Michael Biggie Morgan (from left)GenreRealityStarring Pauly D Gerard Big Jerry Gialanella Jason JROC Craig Michael Biggie Morgan Ryan Labbe Theme music composerPauly D (feat. Dash)Opening themeNight of My LifeCountry of originUnited StatesOriginal languageEnglishNo. of seasons1No. of episodes12ProductionExecutive producers Jacquelyn French Janay Dutton L...

French inventor and Father of Cinematography For the composer, see Louis Le Prince (composer). Louis Le PrinceLe Prince c. early 1860sBornLouis Aimé Augustin Le Prince(1841-08-28)28 August 1841Metz, July MonarchyDisappeared16 September 1890Dijon, French Third RepublicStatusDeclared dead on 16 September 1897 (aged 56)Occupation(s)Artist, art teacher, inventorSpouse Elizabeth Le Prince-Whitley (m. 1869)ChildrenAdolphe Louis Aimé Augustin Le Prince (...

British composer Ella Spira at the Grammy Awards 2016 Ella Spira MBE is a Grammy-nominated composer, visual artist and an award-winning theatre producer based in London, England.[1] Spira co-founded the production company Sisters Grimm alongside ex Royal Ballet ballerina Pietra De Mello-Pittman in 2009.[2] Spira writes and composes music for ballet and film, and works as an arranger making dance remixes for popular UK artists, but her main focus remains Sisters Grimm productio...

Maharaja of Manipur from 1941 to 1949 Maharaja BodhchandraPreparation for the coronation of Maharaja Bodh Chandra Singh, by his Prime Minister in 1944Born(1908-07-24)24 July 1908[1]Imphal, Kingdom of Manipur, British IndiaDied9 December 1955(1955-12-09) (aged 47)[2]Imphal, Manipur, IndiaOccupationMaharaja of Manipur Kingdom of Manipur Part of History of Manipur Kings of Manipur Loiyumba 1074–1112 Senbi Kiyamba 1467–1508 Koirengba 1508–1512 Khagemba 1597–1652 Pitam...

Kodkod[1] Status konservasi Rentan (IUCN 3.1)[2] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mammalia Ordo: Carnivora Famili: Felidae Genus: Leopardus Spesies: L. guigna Nama binomial Leopardus guigna(Molina, 1782) Sinonim Oncifelis guigna, the former classification kodkod (Leopardus guigna), juga disebut Guina, adalah kucing terkecil di Amerika dan juga memiliki penyebaran terkecil, yang ditemukan terutama di tengah dan selatan Chili dan marginal d...

Protected area in South AustraliaLathami Conservation ParkSouth AustraliaIUCN category Ia (strict nature reserve)[1] The conservation park protects Glossy Black Cockatoo habitatLathami Conservation ParkNearest town or cityParndana[2]Coordinates35°38′54.24″S 137°14′11.76″E / 35.6484000°S 137.2366000°E / -35.6484000; 137.2366000[1]Established1 October 1987 (1987-10-01)[3]Area11.75 km2 (4.5 sq mi)&...




















